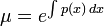http://goo.gl/WmouU
베셀의 미분방정식(Bessel's differential equation)
[경고] 아래 글을 읽지 않고 "베셀 미분방정식"을 보면 바보로 느껴질 수 있습니다.
1. 스투름-리우빌 이론
2. 프로베니우스 방법의 적용
3. 천장에 매달린 사슬의 운동방정식
베셀(Friedrich Wilhelm Bessel)이 일반화 시킨 다음 미분방정식을 베셀의 미분방정식(Bessel's differential equation)이라 한다.
 (1)
(1) (2)
(2)재미있는 것은 베셀의 대학원 지도교수가 가우스(Carl Friedrich Gauss)란 것이다. 우리를 힘들게 하는 베셀 함수(Bessel function)를 만든 베셀이지만 대학원 시절에는 깐깐한 지도교수 밑에서 고생을 겁나게 했으리라...
천장에 매단 사슬(hanging chain)의 움직임[3]을 연구하던 베르누이(Daniel Bernoulli)가 1732년에 처음으로 제안하고(베르누이가 제안한 것은 식 (11)에 있는 0차 제1종 베셀 함수) 베셀이 1824년에 일반화시킨 유명한 베셀 함수는 식 (1)이나 (2)의 해로 정의한다[2]. 당연한 말이지만 베셀 함수의 대부분 성질은 식 (1)이나 (2)를 통해 증명할 수 있다.
식 (1)의 베셀 미분방정식은 다음과 같은 프로베니우스 방법을 위한 미분방정식 관점으로 풀 수 있다.
 (3)
(3)여기서 p(x), q(x)는 발산하지 않는다. 식 (1)과 (3)을 비교하면 p(x) = 1, q(x) = x^2 - n^2이 되어 발산하지 않는다. 식 (4)에 있는 지표방정식(indicial equation)을 이용하면 지표값 r은 다음처럼 결정된다.
 (4)
(4) (5)
(5).svg/500px-Bessel_Functions_(1st_Kind,_n=0,1,2).svg.png)
r1 = n이라 정하면 베셀 미분방정식의 첫번째 해는 다음식으로 구할 수 있다.
 (6)
(6) (7)
(7)식 (7)에 r1 = n을 대입하면 다음 재귀관계(recursion relation)을 얻을 수 있다.
 (8)
(8)그러면 식 (8)의 마지막식을 식 (6)에 대입해 첫번째 해를 구할 수 있다.
 (9)
(9)여기서 !는 계승(階乘, factorial)을 의미한다.
식 (9)와 같은 첫번째 해는 식 (10)처럼 표기하고 제1종 베셀 함수(Bessel function of the first kind)라 부른다. 다음 조건처럼 a0를 정하자. (∵ a0는 임의이므로 아무값이나 넣을 수 있는데 식 (9)를 간단하게 표기할 수 있는 방식으로 a0를 정하자.)
 (10)
(10)식 (10)의 정의를 식 (9)에 대입하면 제1종 베셀 함수를 완전히 얻을 수 있다.
 (11)
(11)식 (10)의 정의로 인해 제1종 베셀 함수는 간편하게 표기할 수 있다.
미분방정식 (1)에서 n이 정수가 아닌 실수라면 보통 ν로 표기한다. 계승의 일반화인 감마 함수(gamma function)를 이용하면 식 (11)을 일반화할 수 있다.
 (12)
(12) (13)
(13)식 (13)을 식 (11)에 대입하면 일반화된 제1종 베셀 함수를 정의할 수 있다.
 (14)
(14)프로베니우스 방법에서 r2 = -n을 대입하면 두번째 해를 얻을 수도 있다. 하지만, 다음 베셀 함수 관계로 인해 첫번째 해와 종속되어버린다. 아래식의 증명은 [여기]에서 볼 수 있다.
 (15)
(15)하지만, n이 정수가 아니면 J_ν(x)와 J_(-ν)(x)는 서로 독립적인 관계가 된다. (∵ 식 (14)의 분모에 있는 감마 함수가 무한대가 되는 경우가 생기지 않는다.) 즉, J_(-ν)(x)가 두번째 해가 된다.
.svg/500px-Bessel_Functions_(2nd_Kind,_n=0,1,2).svg.png)
식 (15)를 바탕으로 제2종 베셀 함수(Bessel function of the second kind)를 정의해보자[1].
 (16)
(16)제2종 베셀 함수는 노이만 함수(Neumann function)라고도 한다. J_ν(x)와 J_(-ν)(x)는 서로 독립이기 때문에 ν ≠ n인 경우 타당한 두번째 해가 된다. 물론 프로베니우스 방법을 이용해 두번째 해를 다음처럼 구할 수도 있다.
 (17)
(17)하지만, 상미분방정식 해의 존재성과 유일성이 있는데 굳이 식 (17)처럼 어려운 길을 갈 필요는 없다. 2차 상미분방정식의 독립적인 해는 두가지이므로 식 (14)와 (16)의 선형결합으로 식 (17)이 표현된다.
식 (16)처럼 제2종 베셀 함수를 지저분하게 정의하는 이유는 ν = n인 경우에도 써먹기 위해서다. 식 (16)에 극한(limit)을 취하면 정수차수(integer order) 제2종 베셀 함수를 정의할 수 있다[1].
 (18)
(18)그러면 식 (15)에 의해 식 (18)의 분자와 분모가 0이 되어서 함수값이 존재하게 된다. 로피탈의 정리(L'Hôpital's rule)를 써서 식 (18)을 계산하자.
 (19)
(19)식 (19)를 계산하기 위해 식 (14)에 있는 베셀 함수를 차수에 대해 미분해보자.
 (20)
(20)여기서 ψ(·)는 다이감마 함수(digamma function)이다.
식 (20)의 결과를 식 (19)에 대입하자.

(21)
기가 막힌 방법으로 식 (21)을 얻었지만 식 (21)에는 다소 문제가 있다. m ≤ n-1인 경우 (m-n)!과 ψ(m-n+1)이 발산하기 때문에 대책이 필요하다. (∵ ψ(m-n+1)이 발산하는 것은 식 (24)를 봐도 자명하다.) 이 문제를 해결하려면 식 (22)에 있는 오일러의 반사공식(Euler's reflection formula)을 이용해야 한다[1].
 (22)
(22)또한, 식 (21)에서 발산하여 문제가 되는 부분은 다음처럼 바꾼다.
 (23)
(23)식 (23)의 우변에 식 (22)를 대입하여 미분하면 다음을 얻을 수 있다.
 (24)
(24)식 (24)를 이용하면 식 (21)에 나오는 무한급수(infinite series)를 단순화시킬 수 있다.
 (25)
(25)그러면 정수차수 제2종 베셀 함수를 아래처럼 표현할 수 있다.
 (26)
(26)참 먼 길을 달려왔다. 식 (26)의 정수차수 제2종 베셀 함수를 유도하는 것은 쉬운 일이 아니다. 오죽 힘들면 약 120년전에 나온 수학논문지[1]에 위 과정이 실렸겠는가! 그래서, 대부분의 공학수학책에는 이 증명을 소개하지 않는다. 위의 유도과정없이 식 (26)을 보면 마법이다. 우리가 근접할 수 없는 무언가를 가지고 있는 것 같다. 하지만, 식 (18)부터 (26)까지 따라가 보면 그냥 수학적 과정을 이어나가서 결과를 얻고 있다.
위의 정의 (14), (16)과는 다르게 식 (1)의 해를 구할 수도 있다. 식 (14)와 (16)을 복소수(complex number)를 이용해 연결하면 다음과 같은 한켈 함수(Hankel function)가 된다.
 (27)
(27)[참고문헌]
[1] M. Bocher, "On Bessel's functions of the second kind," Ann. Math., vol. 6, no. 4, pp. 85-90, Jan. 1892.
[2] G. N. Watson, A Treatise on the Theory of Bessel Functions, Cambridge University Press, 2nd ed., 1944.
[3] C. Byrne, Notes on Bessel's Equation and the Gamma Function, University of Massachusetts Lowell, April 2009.
[다음 읽을거리]
1. 베셀 함수
2. 베셀 함수의 점근식
'수학 (Mathematics) > 공업수학' 카테고리의 다른 글
| 적분인자(integrating factor)를 구할 때 적분상수를 넣지 않는 이유 (0) | 2012.11.03 |
|---|---|
| 수학사이트 (0) | 2012.11.03 |
| 일반해, 특수해 (0) | 2012.11.03 |
| 급수해의 존재 정리(영상강의) (0) | 2012.11.03 |
| 적분 12 : 고급 정적분 테크닉 - 미분 (1) (0) | 2012.11.03 |











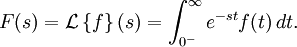
 를 간단히 나타낸 것이고 복소수
를 간단히 나타낸 것이고 복소수  , σ와 ω는 실수이다.
, σ와 ω는 실수이다. 로 표기하기도 한다.
로 표기하기도 한다.
 = sF(s) - f(0)
= sF(s) - f(0) = s^2F(s) - sf(0) - f'(0)
= s^2F(s) - sf(0) - f'(0)
 = - d/ds F(s)
= - d/ds F(s) = (-1)^n d^n/ds^n F(s)
= (-1)^n d^n/ds^n F(s) , L{ f(t) } = F(σ)
, L{ f(t) } = F(σ)

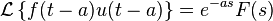
















 Laplace Transform -3.pdf
Laplace Transform -3.pdf


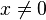 일 때 공통인자
일 때 공통인자 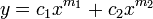

![y=x^{u}\left[A\cos\left(v\ln x\right)+B\sin\left(v\ln x\right)\right], m_{1}=u+iv, m_{2}=u-iv](http://upload.wikimedia.org/math/2/f/c/2fc86b15da84abf60b1d894ed0eecc36.png)















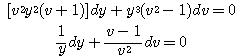
 )
)


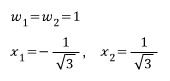
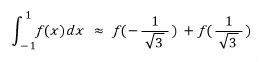


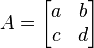

 )).
)).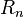 의 벡터로 파악하여, 순서있는
의 벡터로 파악하여, 순서있는  개의
개의  가 행렬
가 행렬  로 표현되고,
로 표현되고,  가
가  의 부피는
의 부피는  로 주어진다. 일반적으로, 선형사상
로 주어진다. 일반적으로, 선형사상  이
이  행렬
행렬  로 주어진다.
로 주어진다.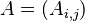 가 정사각행렬이라 하자.
가 정사각행렬이라 하자.



 한 번 행을 바꾼 행렬)
한 번 행을 바꾼 행렬)  (원래 행렬)
(원래 행렬)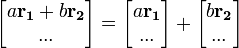
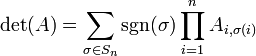
 의 모든 치환(permutation)인
의 모든 치환(permutation)인  에 대해 이루어지고,
에 대해 이루어지고,  는 치환의 부호로 우치환(짝치환, even permutation)일 때 +1, 기치환(홀치환, odd permutation)일 때 -1의 값을 갖는다.
는 치환의 부호로 우치환(짝치환, even permutation)일 때 +1, 기치환(홀치환, odd permutation)일 때 -1의 값을 갖는다.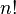 의 합을 포함하고 있어서,
의 합을 포함하고 있어서,  일 때는 실제적으로 사용하기 힘들다.
일 때는 실제적으로 사용하기 힘들다.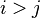 일 때, 혹은
일 때, 혹은  일 때,
일 때,  이면,
이면,  이다.
이다. 행렬을 얻었다면,
행렬을 얻었다면,  이다.
이다. 를 곱하여
를 곱하여  이다.
이다. 이다.
이다. 이다.
이다. 이므로 모든 n-by-n 행렬
이므로 모든 n-by-n 행렬  에 대해 다음 식이 성립한다.
에 대해 다음 식이 성립한다.


 와 함수
와 함수  가 정의되어 있으며,
가 정의되어 있으며,
 를 찾으라는 문제가 주어졌다고 하자.
를 찾으라는 문제가 주어졌다고 하자.  일 때 해는
일 때 해는  를 찾을 수 있다고 하면,
를 찾을 수 있다고 하면,
 는
는 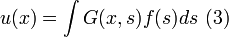
 에 대하여 거리가
에 대하여 거리가  ,
,  인 경우 운동법칙을 다음과 같이 나타낼 수 있다.
인 경우 운동법칙을 다음과 같이 나타낼 수 있다.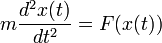
 에 대한 함수
에 대한 함수 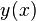 에 대해,
에 대해,  , y의
, y의 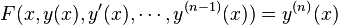
 는 y의 k차 도함수), 이 방정식을 n차 상미분 방정식이라고 정의한다.
는 y의 k차 도함수), 이 방정식을 n차 상미분 방정식이라고 정의한다.




 , (
, (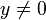 이면,
이면,  )
) 이면 자명한 해
이면 자명한 해 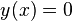 를 얻는다.
를 얻는다.





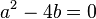
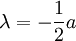
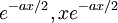






 가 '0'이 아닌 경우를 말한다. 비제차 상미분 방정식의 일반해는
가 '0'이 아닌 경우를 말한다. 비제차 상미분 방정식의 일반해는
 를 배제하고, 제차방정식이라 생각하고 그 식의 일반해
를 배제하고, 제차방정식이라 생각하고 그 식의 일반해  를 구한다.
를 구한다.



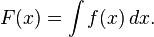
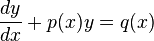
 에 달려있다.
에 달려있다.