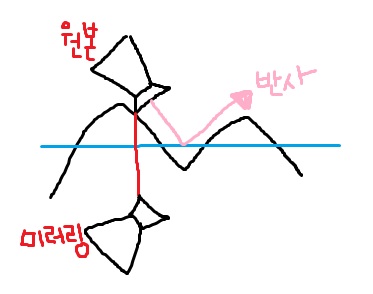
구글링하다 찾은 펄린노이즈
알려진 펄린노이즈의 방법은 전체적인 대강의 윤곽은 비슷 할 수 있찌만 내부적으로 세세히 조금씩 다른
방법들이 있는데 아래 필자가 쓴 방법이 좀더 빠른 연산을 보인다고 한다
tip : 일부 내적에 대한 부족한 설명을 '편집' 이라는 부분에 보충 설명을 해놓음
1차로 예를 들면..
펄린노이즈는 각 정수 단위 사이에들어오는 성분(x) 에 대해서 -1 ~1 사이의 난수 값을 생성해 낸다
각 구간마다 난수벡터를 만들어 놓고 성분(x) x 가 어느 정수 구간 1 거리 사이안에 들어 간다면
ex( 244 ~255) 이 구간 244 와 255 에 설정되어 있는 난수값과 244 와 255 에서 x 값을 향하는 벡터와의 각 내적
값들을
3차 방정식이 x 축이 되는 x ----- > 3차 --------> 선형 보간----------- > v0 ~ v1 의
값으로 보간 되는
즉 일반적으로 선형 보간 된 값이 v0 또는 v1 쪽으로 더 쏠리는 보간값의 형태가 되어
최종 결과 값은 v0 와 v1 의 중간 값보다는 v0 쪽이나 v1 쪽에 더 영향을 받는 난수 값을 얻게 된다
2차는 1차 사이의 보간을 통해
3차는 2차 사이의 보간을 통해 구한다
http://webstaff.itn.liu.se/~stegu/TNM022-2005/perlinnoiselinks/perlin-noise-math-faq.html#toc-algorithm
The
Perlin noise math FAQ
v.
1.0, last updated February 2001
Table
of Contents
So
far, I have found two really great sources for
information about Perlin noise. They are Ken Perlin's Making Noise web site, which has a comprehensive
introduction to the topic, and Hugo Elias's page,
which features some
algorithms and a few more detailed examples of
applications. This document is intended to complement those two
valuable resources by
explaining in more depth, hopefully in plain English, some of the math involved
in Ken Perlin's original implementation of Perlin noise.
I
wrote a demo program in C++ that includes a Perlin noise texture class, which I
hope provides a decent example of C++
code for Perlin noise. You can find the demo at http://www.robo-murito.net/code.html.
If
I've made any grave errors or you just
want to comment, feel free to email me.
Perlin
noise is function for generating coherent noise over a space. Coherent noise means that for any two points in the
space, the value of the noise function changes smoothly as you move from one
point to the other -- that is, there are no
discontinuities.


Non-coherent noise (left) and Perlin noise
(right)
When
I talk about a noise function, I mean a function that takes a coordinate in some
space and maps it to a real number between -1 and 1. Note that you can make
noise functions for any arbitrary dimension. The noise functions above are
2-dimensional, but you can graph a 1-dimensional noise function just like you
would graph any old function of one variable, or consider noise functions
returning a real number for every point in a 3D space.
These
images were all created using nothing but Perlin noise:



Besides
these trivial images, there are countless interesting applications for noise in
computer graphics. Look at Hugo Elias' page or Ken Perlin's
pages for some pretty examples, in-depth
explanations and nifty ideas.
I've
seen implementations
on the
internet that take non-coherent noise, as
shown above,
and smooth it (with something like a blur function) so it becomes coherent
noise, but that can end up being more computationally expensive
than the function I'll present here, which is more
or less theoriginal implementation that Ken Perlin came
up with.
The problem with Perlin's implementation on its own was that that reading the
descriptions of the math published on Perlin's website was a bit
like reading Greek --
it took me about a week of reading his code and notes to figure out the actual
geometric interpretations of the math. So hopefully this document can trim
down that
learning curve.
Let's
look at the 2D case, where we have the function
noise2d(x, y) = z,
with x, y,
and z all real (floating-point) numbers. We'll
define the noise function on a regular grid, where grid points are defined
for
each whole number,
and any number with a fractional
part (i.e. 3.14) lies
between grid points.
Consider finding the value of noise2d(x, y),
with x and y both
notwhole
numbers -- that is, the point (x, y)
lies somewhere in the middle of a square in our grid. The first thing we do is
look at the gridpointssurrounding (x, y).
In the 2D plane, we have 4 of them, which we will call (x0, y0),
(x0, y1),
(x1, y0),
and (x1, y1).

The 4 grid points bounding (x, y)
Now
we need a function
g(xgrid, ygrid) =
(gx, gy)
which takes each
grid point and assigns it
a pseudorandom
gradient of length
1 in R2 ('gradient' is just the name for an ordered
pair or
vector that we think of as pointing in a particular direction).
By pseudorandom,
we mean
that g has the appearance of randomness, but
with the important
consideration that it always returns the same gradient for the same
grid
point,
every time it's calculated. It's also important that every direction
hasan equal
chance of being
picked.

The 4 pseudorandom gradients associated with the
grid points
Also,
for each grid point, we generate a vector going from the grid point to
(x, y), which is easily
calculated by subtracting the grid point from (x, y).

Vectors from the grid points to (x, y)
Now
we have enough to start calculating the value of the noise
function at (x, y). What
we'll do is calculate the influence of each pseudorandom gradient on the final
output, and generate our output as a weighted average of those influences.
First
of all, the influence of each gradient can be calculated by performing a dot
product of the gradient and the vector going from its associated grid point to
(x, y). A refresher on
the dot product -- remember, it's just the sum of the products of all the
components of two vectors, as in
(a, b) · (c, d) = ac + bd .
Since
I'm really tired of writing subscripts, we'll just refer to these 4 values
as s, t, u,
and v,
where
s = g(x0, y0) · ((x, y) - (x0, y0)) ,
t = g(x1, y0) · ((x, y) - (x1, y0)) ,
u = g(x0, y1) · ((x, y) - (x0, y1)) ,
v = g(x1, y1) · ((x, y) - (x1, y1)) .
So
here's a 3D-ish picture of some influences s, t, u,
and v coming out of the R2 plane (note that these probably wouldn't be
the actual values generated by the dot products of the vectors pictured
above).

Influences from the grid points
Geometrically,
the dot product is proportional to the cosine of the angle between two
vectors
, though
its unclear to me
------------------------------------------------------------------------------------------
편집
: 다른 곳에서 보니....
내적이
의미 하는게 사각 셀(사각형 안의 x,y 에 해당하는) 것의 4 귀퉁위의 각 높이값을
말하는 듯..
------------------------------------------------------------------------------------------
if
that geometrical interpretation helps one visualize what's going on. The
important thing to know at this point is that we have four numbers, s, t, u, and v which are uniquely determined by
(x, y) and the
pseudorandom gradient function g. Now we need a way to combine them
to get noise2d(x, y), and as I suggested before, some
sort of average will do the trick.
I'm
going to state the obvious here and say that if we want to take an average of
four numbers, what we can actually do is this:
- find the average of the first pair of numbers
- find the average of the second pair of numbers
- average those two new numbers together
--
and that's the strategy we'll take here. We'll average the "front" values s and t first, then average the "rear" values u and v.
This works to our advantage because the points below s and t,
and similarly below u and v vary only in the x dimension -- so we only
have to worry about dealing with one dimension at a time.
We're
not taking a plain vanilla-flavored average here, but instead, a weighted
average. That is, the value of the noise function should be influenced more
by s than t when x is closer to x0 than x1 (as is the case in the pictures above). In
fact, it ends up being nice to arrange things so that x and y values behave as if they are slightly closer
to one grid point or the other than they actually are because that has a
smoothing effect on the final output. I know that sounds really silly, but noise
without this property looks really stupid. In fact, it sounds so silly that I'm
going to write it again: we're going
to want the input point to behave as if its closer to one grid point or another
than it actually is.
This
is where we introduce the concept of the ease curve. The function
3p² - 2p³ generates a nice S-shaped curve that has a few
characteristics that are good for our purposes.

Meet the ease curve
What
the ease curve does is to exaggerate the proximity its input to zero or one. For
inputs that are sort of close to zero, it outputs a numberreally close to zero. For inputs close to one, it
outputs a number really close to one. And when the input is exactly
one half, it outputs exactly one half. Also, it's symmetrical in the sense that
it exaggerates to the same degree on both sides of p = ½. So if we can treat one grid point as
the zero value, and the other as the one value, the ease curve has the exact
smoothing effect that just we said we wanted.
Ok,
I've droned on long enough, it's calculation time: first, we take the value of
the ease curve at x - x0 to get a weight Sx. Then we can find the
weighted average of s and t by constructing a linear function that maps
0 to s and 1 to t, and evaluating it at our x
dimension weight Sx.
We'll call this average a. We'll
do the same for u and v, and call the result b.



Finding
the first two averages using linear interpolation
The
above figures should satisfy you that no matter where x happens to fall in the grid, the final
averages will always be between s and t, and u andv, respectively. Mathematically,
this is all simple to calculate:
Sx = 3(x - x0)² - 2(x - x0)³
a = s + Sx(t - s)
b = u + Sx(v - u)
Now
we find our y dimension weight, Sy,
by evaluating the ease curve at y - y0,
and finally we take a weighted sum of a and b to get our final output value z.


A weighted
sum of the first two averages yields the final output
And
there you have it. So all you have to do is call the noise function for every
pixel you want to color, and you're done. Probably.
...and they all lived happpily ever after.
The End.
An
interesting consequence of all of this is that the noise function becomes zero
when x and y are both whole numbers. This is because the
vector (x, y) - (x0, y0) will
be the zero vector. Then the dot product of that vector and g(x0, y0)will
evaluate to zero, and the weights for the averages will also always be zero, so
that the zero dot product will influence the final answer 100%. The funny thing
is that looking at the noise function, you would never guess that it ends up
being zero at regular intervals.
If
you want to extend the noise function to n dimensions, you'll need to consider
2n grid points, and perform 2(n - 1) weighted sums. The implementation presented
here has a computational complexity of O(2(n - 1)),
which means that you'll really start to drag if you want to look at 5-, 6-, or
greater dimensional noises.
We
could increase the speed of the noise function if we didn't have to compute the
pseudorandom gradient every time we called the noise function (because for
every x between some x0 and x1 and y between some y0 and y1,
we have to recalculate the same four gradients every time the noise function is
called!) The nice thing to do would be to precalculate the gradient for every
possible (xgrid, ygrid),
but xgrid and ygrid are allowed to vary all over the real plane!
How could we possible precalculate every value?
The
neat thing about noise is that it's locally variable, but globally flat -- so if
we zoom out to a large degree, it will just look like a uniform value (zero in
fact). So, we don't care if the noise function starts to repeat after large
intervals, because once you're zoomed out far enough to see the repeat, it all
looks totally flat anyways.
So
now we should feel justified in doing a little trick with modulus. Say we're
doing noise in 3D, and we want to find the gradient for some grid point
(i, j, k). Let's precompute a permutation table P, that maps every integer from 0 to
255 to another integer in the same range (possibly even the same number). Also,
let's precompute a table of 256 pseudorandom gradients and put it in G, so that G[n] is some 3-element
gradient.
Now,
g(i, j, k)
= G[ ( i + P[ (j + P[k]) mod 256 ] ) mod 256
]
But
on a computer, modulus with 256 is the same thing as a bitwise and with 255,
which is a very fast operation to perform. Now we've reduced the problem of a
possibly involved function call into nothing but some table lookups and bitwise
operations. Granted, the gradients repeat every 256 units in each dimenstion,
but as demonstrated, it doesn't matter.
This
speedup is also mentioned on Perlin's web page, and is actually used in his original implementation.
What
if you want to use procedural noise to calculate a repeating animation of a
licking flame or rolling clouds? It is true that noise on it's own doesn't tend
to repeat discernably, and that's great for generating ever-changing images;
however, if you want to prerender an animation, you'll probably want it to
repeat. Given that F is your function that generates a real
number from a point in noise-space, and you want your animation to repeat
every t units, you define a new function that loops
when z is between 0 and t:
Floop(x, y, z)
= ( (t - z) * F(x, y, z) +
(z) * F(x, y, z - t) ) / (t)
Now
each function call takes twice as long to calculate, but since you're probably
not going to use this cycling technique in real time, it probably doesn't
matter.
The
explanation
Consider
the graph of a noise function F(x, y, z) for
some fixed x and y. The problem is, you want F(0) = F(t) and there is no guarantee
that will be the case with any old x, y, and t. Actually, since any given x and y should have no influence on the repeating
aspect of the animation, we can for all practical purposes throw them out while
we're developing our repeating function, and consider the simplified case of a
one-dimensional noise function F(z).

A one-dimensional noise function
We
need to take this function and change it into one where it is guaranteed
that F(0) = F(t). Here's an expanded view
of our noise function showing its behavior from -t to t:

The same, function, ranging over a positive and
negative domain
Now
we define a new function F'(z) that behaves like F(z) when z is near zero, but behaves like F(z - t) when z is near t. If you think about it, you see
that F'(0) = F(0), and that F'(t) = F(t - t) = F(0). We can do this with a simple
linear interpolation by considering a linear function which is equal to F(z) at 0, and equal to F(z - t) at t.
High
school algebra tells us that this linear function has a slope of
(rise)
/ (run) = (F(z - t) - F(z)) / (t - 0) = (F(z - t) - F(z)) / t
and
an intercept of F(z).
Now we set up F'
as this linear interpolation operating on z:
F'(z)
= slope(z) + intercept
= (
(F(z - t) - F(z)) / t )(z) + F(z)
= ( (
(z) * F(z - t) - (z) * F(z) ) / t ) + F(z)
= ( (
(z) * F(z - t) - (z) * F(z) ) / t ) + (t / t) * F(z)
= ( (z)
* F(z - t) - (z) * F(z) + (t) * F(z)) / (t)
= ( (z) * F(z - t) + (t-z) * F(z) ) / (t)
= ( (t-z) * F(z) + (z) * F(z - t) ) / (t)
Which
is basically the same as the function given above. If you look at F'
next to F,
you can see that the function does indeed repeat in that F'(0)
= F'(t).
Also notice that the peaks just to the right of F'(0)
are the same as the peaks just to the right of F'(0),
and that the peaks just to the left ofF'(t)
are virtually identical to the peaks just to the left of F(0).


The old
function (left), and the new, repeating function (right)
If
you had a little calculus and too much free time, you could prove that this
looping (and the tiling in the next section) is truly seamless: not only
does F(0) = F'(t), but all their
derivatives should match up as well. Which means that no one should be able to
tell where the repeat actually happens.
Say
you're using a noise function to generate textures for a polygon-based engine.
Chances are, you might want the textures to be tileable. You can extend the
above example to generate tileable 2-dimensional noise that repeats every w units in the x dimension and every h units in the y dimension. This will require
a weighted sum of four calls to the original function (which again, for lack of
imagination, we will call F).
Ftileable(x, y)
= (
F(x, y) *
(w - x) * (h - y) +
F(x - w, y) * (x) *
(h - y) +
F(x - w, y - h) * (x) * (y) +
F(x, y - h) * (w - x) * (y)
) /
(wh)
A
pattern should be emerging here, so it shouldn't surprise you that you'll need
evaluate a weighted sum of 8 calls to the noise function if you want to have a
repeating animation that tiles in the x and y dimenstions. I'm not going to
write it out here out of space considerations, and also because it should be
evident what the sum will be.


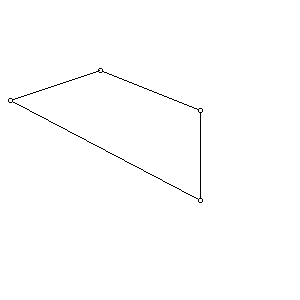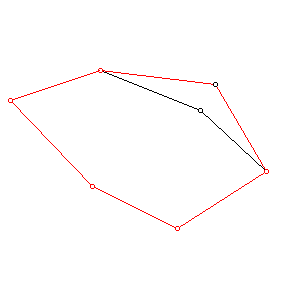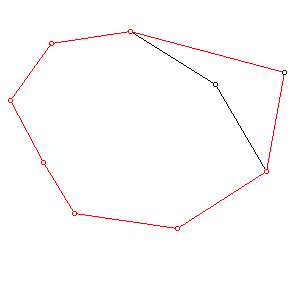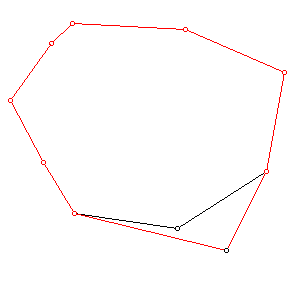
 progressive mesh.pdf
progressive mesh.pdf

























































![[http]](http://www.redwiki.net/wiki/imgs/http.png)
about 7 months ago
You are looking up 10 and not 9 pixels! Coordinate 0.0 intersects two pixels and so you take full advantage of linear interpolation! Else you need to offset by half a pixel!
Where is the benefit of the usual easier way? Lookup at coordinates [-4, -2, 0, 2, 4] to get 10 pixel range and then apply the weighting of each two texels and calculate final value?
about 6 months ago
Hi Daniel,
This article was incredibly clear and informative. Thank you for taking the time to put it together. I’m still learning this stuff, so this was very helpful.
I wrote up a small Python script based on this post to generate the gaussian texture lookups, optimized for linear sampling. Maybe it can be useful to someone else too:
https://gist.github.com/2332010
Thanks again
about 1 month ago
Hey Daniel,
nice article, the connection with Pascal’s triangle is indeed very interesting.
I would like to add two things. First, maybe it would be good to add that Gaussian has a unit integral, since it’s probably one of the reasons the filtering works (in the continuous case at least). The 3D plot should also reflect this (meaning that such a wide Gaussian certainly wouldn’t reach a value of 1.6). This is of course just minor.
The second thing that struck me was:
“A Gaussian function with a distribution of 2σ is equivalent with the product of two Gaussian functions with a distribution of σ.”
This is just my opinion, but I think this doesn’t hold. First, I think such product won’t be a 2σ-Gaussian (properly normalized and all). Second, a repeated application of any filter corresponds to applying their *convolution*, which differs from product. And, convolution of two Gaussians with StD=σ produces a Gaussian with StD=Sqrt(2*σ^2)=σ*Sqrt(2).
I think what you meant was that product of 2 polynoms with order n (n-th row of Pascal triangle) gives you a polynom of order 2n? That should be true.
What do you think?
Oskar
about 1 month ago
You can do a 9-tap gaussian using only 2 texture fetches by sampling at one of corner of the center pixel in the first pass (f.x with an xy-offset of -0.5,0.5 ) and then sample the opposite corner in the next pass ( xy-offset of 0.5,-0.5 )
This results in the standard
121
242
121
9-tap gaussian.
You can do the same gaussian in a single pass if you sample at all 4 corners (4 texture fetches)
You can do a nice and very fast 7-tap blur in a single pass if you sample two opposite corners with an offset of 1/3 away from the center.
This results in a
121
282
121
convolution kernel.
If you calculate the strength of the blur by subtracting from the center pixel you can then scale the result so that it closely matches the regular 9-tap gaussian.
I also do a 17-tap blur using only 5 fetches in a single pass by sampling the center pixel and then offsets (0.4,-1.2) , (-1.2,-0.4) , (1.2,0.4) and (-0.4,1.2).
I then adjust the strength of it to more closely match the 9-tap gaussian.