반응형
3DMP engines
3D그래픽스 물리 수학, 프로그래밍 GPU Shader 게임엔진 알고리즘 디자인패턴 matlab etc..
치환을 사용하는 이유는 우변이 만약 lnx 등으로 나간다면 나중에 이 우변의 항을 적분해야 되는 순간이 오게 되는데 그때의 연산량이 엄청 길다
그래서 치환을 활용하여 길게 나갈껏 같은 연산을 간략하게(원래에 상대적으로 비교하여) 함으로써 풀이를 좀 더 용이하게 할 수 있다
다음과 같은 비동차(비제차) 미분방정식이 있다고 하자
그런데 x 의 차수와 y 의 미분 횟수가 각 항마다 동일하고 계수가 상수가 아니기 때문에 (좌변이..)
코시 오일러 미분방정식을 사용할 수 있고
우변이 lnx 로 가기 때문에 나중의 적분을 고려하여 비교적 간략하게 치환을 활용한
미분방정식 풀이를 이용 할 수 있겠다
정리하자면 코시의 오일러 미방으로 동차 fy)=0 를 만족하는 해 Y_c 를 구한 후 특수해 y_p 를 구해
이 둘을 더해주는 방식으로 풀면 된다, 이때 특수해는 매개변수 변환법을 사용해 구한다
f(y)=g(x) ( f(y) 가(=) 0 이 아닐때)
그런데 ...
g(x) 가 다항함수, 지수함수, cos,sin 일때는 미분방정식의 특성방정식 을 통하여
g_zero(x)g(x)=g_zero(x)0 = 0 이 되는 해 t 의 값을 구해 t 를 지수로 같는 e^f(x) 꼴의 함수들을 구해
일반해를 만들 수 있다 또한 어떠한 해와 관련된 힌트가 있다면 해당 개수를 구하는 미정개수법으로
상수를 구할 수다
하지만, 현재는 우변이 ln 과 같은 log 가 있기 때문에 특성방정식으로 구할 순 없으며 대신
매개변수 변환법으로 특수해(y_p) 를 구해야 한다
최종해는 y = y_c + y_p 가 된다
참고 : 코시의 오일러 미분방정식의 일반해의 꼴이 x^m 의 꼴로 나타난다 x^m 이 여러개로 연결되는 형태..
또한 동차 미분방정식 f(y) = 0 의 일반해의 꼴은 x^(D)e^f(x) 의 꼴 이거나 저것과 결합된 cos+sin 형태로
[D 는 정수집합, x^(D)e^f(x) 꼴이라는 것은 이것들이 여러개로 결합될 수 있다는 것 + 기호로..]
나타난다 자세한건 동차미분방정식의 증명과정을 참고하면 된다
p.s 위 식의 풀이를 적으려다가.. 풀이가 제법 길기도 하거니와 여기까지 쓰면서 귀차니즘 등으로
이 이상의 기술을 멈췄는데 만약 댓글로 요청이 있으면 풀이를 수식기를 활용하여 올리겠습니다
아래부터는 첨부내용
코시-오일러 방정식
위키백과, 우리 모두의 백과사전.
코시-오일러 방정식(혹은 오일러-코시 방정식: Euler-Cauchy equation)은
- x2y'' + axy' + by = 0
와 같은 선형 상미분방정식인데, 주어진 상수 a와 b 그리고 y(x)를 가진다.
- y = xm
이라고 하고, 첫 번째 식에 대입하면,
- x2m(m − 1)xm − 2 + axmxm − 1 + bxm = 0
이 되고, 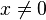 일 때 공통인자 xm을 제거하면,
일 때 공통인자 xm을 제거하면,
- m2 + (a − 1)m + b = 0
이 된다.
여기서 m에 따라 미분방정식의 해를 구할 수 있다.
| case | 해 |
|---|---|
| 서로 다른 두 실근 | 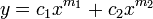 |
| 중근 |  |
| 공액 복소근 | ![y=x^{u}\left[A\cos\left(v\ln x\right)+B\sin\left(v\ln x\right)\right], m_{1}=u+iv, m_{2}=u-iv](http://upload.wikimedia.org/math/2/f/c/2fc86b15da84abf60b1d894ed0eecc36.png) |
반응형
'수학 (Mathematics) > 공업수학' 카테고리의 다른 글
| 비선형 미분방정식 [기초] (0) | 2012.11.03 |
|---|---|
| 비감쇠 강체운동 미분방정식(상계수미방-미정개수법으로 풀이) (0) | 2012.11.03 |
| 특성방정식 (0) | 2012.11.03 |
| 크래머 공식 순서와 변수변환법 3차에서 에서 왜 0,0,f(x) 로 놓고 푸는지... (0) | 2012.11.03 |
| 변수변환법(매개 변수 변환법) (0) | 2012.11.03 |

