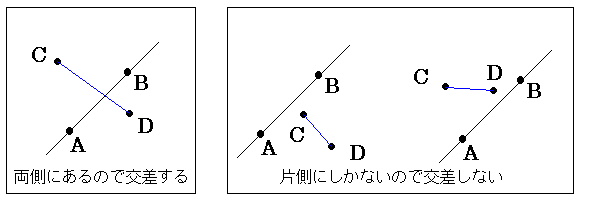
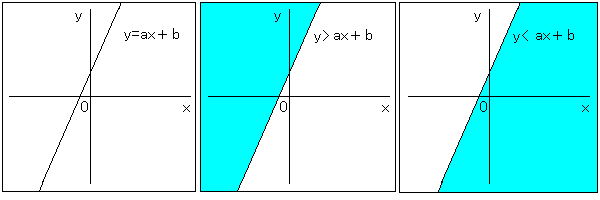
처음에
저는 쿼터니언이라는 용어가 마치 비밀스러운 어둠의 힘을 가지고 있는 암흑물체에 관한 양자론 용어처럼 느껴집니다. 여러분도 역시 이 어둠의 힘에 매료되었다면 이 글이 도움이 될 것입니다(그렇게 되기를 바랍니다). 이 글은 쿼터니언을 이용해서 회전을 하는 방법을 보여주어 쿼터니언을 좀더 쉽게 이해하는데 도움을 줄 것입니다. 만약 여러분이 글에서 잘못된 내용을 발견하시면 robin@cyberversion.com로 메일을 보내주세요. 또, 이 기사를 여러분의 사이트에 실으려고 하신다면 저에게 메일을 보내주세요. 저는 저의 글이 어디에 퍼져있는지 알고 싶답니다.
왜 쿼터니언을 사용할까?
이 질문에 대답하기 위해서 우선 방향을 나타내는 일반적인 방법에 대해 논의해 보도록 합시다.
오일러 표현
이것이 현재까지 알려진 방법중 방향을 나타내는 가장 간단한 방법입니다. 오일러 표현은 각각의 축마다 축주위의 회전량을 가지고 있습니다. 따라서, 다음과 같은 0도에서 360도(혹은 0~2π)의 범위에서 변하는 3개의 값을 가집니다.
x, y, z <-- 전역 좌표축 주위의 회전 각도
이 값은 각각 롤, 피치, 요(혹은 피치, 롤, 요, 등 등)를 표현합니다. 방향은 3개의 각도로부터 생성되는 3개의 회전 행렬을 지정한 순서대로 곱해서 구할수 있습니다.
Note: 회전은 전역 좌표계의 좌표축을 기준으로 회전합니다. 즉 최초의 회전이 그 후의 2번째 3번째의 회전축에 영향을 주지 않습니다. 이 때문에 짐벌락(gimbal lock) 문제가 발생하게 됩니다. 짐벌락에 대해서는 조금 후에 자세히 설명하겠습니다.
회전축과 각도(Axis Angle)에 의한 표현
이 방법은 짐벌락을 피할수 있으므로 오일러각 방법보다 좀더 낫습니다. 회전축과 각도에 의한 표현은 임의의 회전축을 나타내는 단위 벡터와 단위 벡터 주위의 회전을 나타내는(0~360) 값으로 구성됩니다.
x, y, z <-- 임의의 축을 나타내는 단위 벡터 angle <-- 바로 윗줄에서 정의한 축 주위로 회전 각도
왜 이 방법이 나쁠까요?
짐벌락
오일러 표현에 있어서 회전은 전역 좌표계에서 일어나기 때문에 한 축의 회전이 다른 축의 회전과 겹치는(override) 문제가 발생합니다. 따라서 회전을 할 수 있는 축 하나를 잃게 됩니다. 이것을 짐벌락이라고 합니다.
예를 들어, X축과 평행한 어떤 벡터를 Y축주위로 회전해서 그 벡터가 Z축과 평행하게 되었다고 하면 이 때, Z축주위로 아무리 회전시켜도, 벡터의 방향은 전혀 변하지 않게 됩니다.
나중에 여러분에게 짐벌락의 예와 쿼터니언을 사용해서 짐벌락을 해결하는 방법을 보여드리겠습니다.
보간 문제
회전축 표현이 짐벌락 문제로 부터 자유롭긴 하지만 두개의 회전을 보간하는 경우, 또 다른 문제가 발생합니다. 보간계산을 마친 회전들이 부드럽지 못하여 회전 애니메이션이 삑사리가 날 수도 있습니다. 오일러 표현도 마찬가지로 이 문제를 가지고 있습니다.
자. 쿼터니언으로 빠져 봅시다 !
시작하기에 앞서, 몇가지 가정을 세우겠습니다. 저는 수학적인 이해가 중요시되는 글에서 수학적인 내용들을 대충 생략해버리는 글들에 진절머리가 납니다. 이런 글들은 독자들을 혼란에 빠뜨리기 쉽상입니다.
좌표계 - 이 글은 OpenGL과 같은 오른손 좌표계를 사용합니다. 만약 여러분이 Direct3D 같은 왼손 좌표계를 사용하고 계시다면 행렬들을 전치(transpose)하셔야 합니다. 이미 Direct3D의 샘플들은 쿼터니언 라이브리러를 가지고 있다는 사실에 유념해주시기 바랍니다. 그럼에도 불구하고 저는 여러분이 그 라이브러리를 사용하시기 전에 그 내부가 어떻게 구성되는지를 한번 짚고 넘어갔으면 하는 바램입니다.
회전순서 - 오일러 표현에서 회전 순서는 X->Y->Z의 순입니다. 행렬 형태로 아래와 같이 표현합니다.
RotX * RotY * RotZ <-- 매우 중요
행렬 - 행렬은 OpenGL 처럼 열우선 방식으로 합니다.
예 [ 0 4 8 12 1 5 9 13 2 6 10 14 3 7 11 15 ]
벡터와 점 - 변환을 위해 벡터와 점은 4x1의 행렬로 표현합니다. 다음과 같은 모습입니다.
회전 행렬 * [ vx vy vz 1 ] <-- 4x1 벡터
저는 특히 Direct3D보다 OpenGL을 선호하지는 않습니다. 그저 제가 OpenGL을 먼저 배웠고, 쿼터니언도 OpenGL을 통해 익혔을 뿐입니다.
Note: 만약 X->Y->Z 순서가 아닌 다른 회전 순서를 지정하면 몇몇 쿼터니언의 함수들을 다시 구현해야 합니다. 특히 오일러 표현을 다루는 함수들이 그렇습니다.
쿼터니언이란 무엇인가?
복소수는 i라는 기호를 사용하여 정의하는 허수(가상의 수)입니다. i는 i * i = -1 라는 성질을 가지고 있습니다.
쿼터니언은 복소수의 확장입니다. i만 사용하는 것이 아니라 제곱근이 ―1 이 되는 3개의 허수를 가집니다. 이 3개의 수는 보통 i, j, k로 표기합니다. 다시 말해 이것은 다음과 같은 성질을 가집니다.
j * j = -1 k * k = -1
따라서 쿼터니언을 아래와 같이 표현할 수 있습니다.
q = w + xi + yj + zk
여기서 w는 실수, x, y, z는 복소수입니다.
흔히 사용하는 또 다른 표현은 아래처럼 벡터형태로 표현할수 있습니다.
q = [ w, v ]
여기서 v = (x, y, z)는 "벡터"라고 말하며 w는 "스칼라"입니다.
v를 벡터라고 부르지만 이것은 일반적인 3차원 벡터가 아닌 4 차원 공간상에 벡터를 표현한 것으로 직관적으로 시각화할 수 없습니다.
항등 쿼터니언
벡터와 다르게 2개의 항등 쿼터니언이 있습니다.
곱 항등 쿼터니언은 아래 처럼 표현합니다.
q = [1, (0, 0, 0)]
그래서 이 곱 항등 쿼터니언과 곱해진 어떤 쿼터니언도 변하지 않습니다.
가산 항등 쿼터니언은 (저희는 사용하지 않습니다)은 아래처럼 표현합니다.
q = [0, (0, 0, 0)]
방향 표현으로 쿼터니언 사용하기
우선 저는 쿼터니언이 벡터가 아니라는 사실을 말씀드리고 싶습니다. 따라서 여기서 벡터 수학을 사용하지 말아주십시요.
이 부분은 매우 수학적인 내용을 다룰 것입니다. 참을성을 가지고 제 설명을 읽어주세요.
우선 쿼터니언의 크기를 정의합니다.
|| q || = Norm(q) = sqrt(w2 + x2 + y2 + z2)
단위 쿼터니언은 아래와 같은 속성을 가지고 있습니다.
w2 + x2 + y2 + z2 = 1
그 때문에 쿼터니언의 정규화는 아래와 같이 구합니다
q = q / || q || = q / sqrt(w2 + x2 + y2 + z2)
이 단위 쿼터니언은 특별합니다. 왜냐하면 단위 쿼터니언은 3D 공간에서 방향을 표현할 수 있기 때문입니다. 따라서 앞에서 논의된 두가지 방법 대신에 단위 쿼터니언을 통해 방향을 표현할 수 있습니다. 단위 쿼터니언으로 방향을 표현하려면 단위 쿼터니언을 다른 표현(예: 행렬)으로 변환하거나 반대로 변환하는 방법이 필요합니다. 이것에 대해서는 곧 설명드리겠습니다.
단위 쿼터니언 시각화 하기
단위 쿼터니언은 (x, y, z) 요소를 임의의 축, w요소를 회전 각도로 하는 4차원 공간상의 회전으로서 시각화할 수 있습니다. 모든 단위 쿼터니언들은 4D 공간에서 단위 길이를 가지는 구를 형성하게 됩니다. 다시한번 이게 무슨 소리지 하고 여러분은 직관적으로 이해가 안되실것입니다. 하지만 제가 정말 말하고 싶은 것은 쿼터니언의 스칼라 요소(w)의 부호를 반전시키는 것만으로 180도 회전한 쿼터니언을 얻을 수 있다는 것입니다.
Note: 단위 쿼터니언만을 방향표현에 사용할 수 있습니다. 이 뒤에 논할 모든 내용은 모두 단위 쿼터니언을 사용한다고 가정합니다.
쿼터니언으로부터의 변환
효과적으로 쿼터니언을 사용하려면 결국 쿼터니언을 다른 표현으로 변환해야 할 필요가 있을 것입니다. 키 눌림을 쿼터니언으로 해석할 수는 없지 않습니까? 할수 있으신 분 계신가요? 글쎄여. 아직까지는 없는 듯 하죠?
쿼터니언에서 행렬로의 변환
OpenGL와 DirectX는 행렬로 회전을 표현하기 때문에 쿼터니언->행렬 변환이 아마 가장 중요한 변환 함수일 것입니다. 왜냐하면 동차 행렬이 3D의 기본 표현이기 떄문입니다.
쿼터니언 회전과 동등한 회전 행렬은 다음과 같습니다.
행렬 = [ w2 + x2 - y2 - z2 2xy - 2wz 2xz + 2wy 0
2xy + 2wz w2 - x2 + y2 - z2 2yz - 2wx 0
2xz - 2wy 2yz + 2wx w2 - x2 - y2 + z2 0
0 0 0 w2 - x2 - y2 + z2]
w2 + x2 + y2 + z2 = 1이 되는 단위 쿼터니언의 속성을 사용하면 위 식을 다음과 같이 간단하게 만들 수 있습니다.
행렬 = [ 1 - 2y2 - 2z2 2xy - 2wz 2xz + 2wy 0
2xy + 2wz 1 - 2x2 - 2z2 2yz - 2wx 0
2xz - 2wy 2yz + 2wx 1 - 2x2 - 2y2 0
0 0 0 1 ]
쿼터니언으로부터 회전축과 각도에 의한 표현으로 변환
한 쿼터니언을 삼차원 공간에서의 임의축 주위의 회전축과 각도에 의한 표현으로 변환하는 방법은 다음과 같습니다.
회전축이 (ax, ay, az)이고 각도가 theta (라디안)이면 각도는 angle= 2 * acos(w)가 됩니다. 그 때 ax= x / scale ay= y / scale az= z / scale 이 됩니다. scale은 scale = sqrt (x2 + y2 + z2)입니다..
제가 알고 있는 다른 방법은 scale = sin(acos(w))을 사용하는 것입니다. 저 스스로 수학적으로 동치관계를 증명하려고 하지는 않았지만 두 방법 다 결과는 같을 것이라 생각합니다.
어쨌든, scale이 0이라면 회전이 없다는 뜻입니다. 그리고 여러분이 특별한 조치를 취하지 않는다면 회전축이 무한대가 됩니다. 따라서 scale이 0인 경우에는 언제나 회전각이 0인 임의의 단위벡터를 그 축에 설정하시면 됩니다.
간단한 예
제가 설명하려고 하는 것들에 대해서 뭐가 뭔지 모르겠다 하시는 독자분들을 위해 이제부터 간단한 예를 보여드리겠습니다.
우선 카메라 방향을 오일러 각으로 표현한다고 해봅시다. 그러면 렌더링 루프에서 다음과 같은 식을 이용하여 카메라를 위치시킵니다.
RotateX * RotateY * RotateZ * Translate
이 때 각각의 요소는 4x4 행렬입니다.
이제 단위 쿼터니언을 사용해서 카메라의 방향을 표현하려면 먼저 쿼터니언을 행렬로 변환해야 합니다. 그러면
(쿼터니언으로부터 변환한 회전 행렬) Rotate * Translate
같은 것이 생기게 됩니다
OpenGL에 특화한 예는 다음과 같게 될것입니다.
| 오일러 | 쿼터니언 |
glRotatef( angleX, 1, 0, 0)
glRotatef( angleY, 0, 1, 0)
glRotatef( angleZ, 0, 0, 1)
// 평행이동 | // 오일러를 쿼터니언으로 변환
// 쿼터니언을 회전축과 각도로 변환
glRotate(theta, ax, ay, az)
// 평행이동 |
위의 표현은 모두 같습니다. 제가 말할려고 하는 것은 방향에 쿼터니언을 사용하는 것은 오일러나 회전축과 각도에 의한 표현과 완전히 같고, 앞서 언급한 변환 함수를 통해 상호교환이 가능하다라는 것입니다.
다만, 위의 쿼터니언에 의한 표현에는 오일러 표현법과 마찬가지로 짐벌락의 위험성이 있습니다.
역자주 – "왜 짐벌락 위험성이 있지"라는 답을 글내용상 알수가 없습니다.
물론, 아직은 회전을 쿼터니언으로 만드는 방법을 모르시겠지만 그것은 아래 부분에서 설명하겠습니다.
Note: Direct3D나 OpenGL를 사용하시는 독자분들은 API가 행렬 연결을 처리해주기 때문에 직접 행렬을 취급하는 일은 없겠지만, 이것에 대해서 알아둘 필요가 있습니다.
쿼터니언 곱
단위쿼터니언이 3D공간에서의 한 방향을 표현하기 때문에 2개의 단위 쿼터니언간의 곱은 2개의 단위 쿼터니언의 회전을 결합한 회전을 나타내는 단위 쿼터니언이 됩니다. 놀라운 일이지만, 사실입니다.
다음과 같은 2개의 쿼터니안이 있다고 가정해봅시다.
Q1=(w1, x1, y1, z1); Q2=(w2, x2, y2, z2);
이 2개의 단위 쿼터니언을 결합한 회전은 아래와 같이 구해집니다
Q1 * Q2 =( w1.w2 - v1.v2, w1.v2 + w2.v1 + v1*v2)
이 때 ,
v1 = (x1, y1, z1) v2 = (x2, y2, z2)
이 됩니다.
여기서 .와 *은 내적과 외적을 나타냅니다.
하지만 위 식을 아래와 같이 최적화할 수 있습니다.
w = w1w2 - x1x2 - y1y2 - z1z2 x = w1x2 + x1w2 + y1z2 - z1y2 y = w1y2 + y1w2 + z1x2 - x1z2 z = w1z2 + z1w2 + x1y2 - y1x2
물론, 여타 쿼터니언들과 마찬가지로 결과 단위 쿼터니언을 다른 회전 표현으로 변환하는 것도 가능합니다. 이런 점이 바로 쿼터니언의 진정한 미학입니다. 2개의 단위 쿼터니언은 구 상에 위치하기 때문에 4차원 공간에서 이들을 곱하는 방법은 짐벌락의 문제를 해결합니다.
여기서 곱하는 순서가 중요합니다. 쿼터니언의 곱은 교환칙이 성립되지 않습니다. 즉 이것은 아래의 식을의미합니다.
q1 * q2 ≠ q2 * q1
Note: 2개의 쿼터니언은 동일한 좌표계 축을 참조해야 합니다. 저는 서로 다른 좌표계에서 2개의 쿼터니언을 합성하는 실수를 범한 적이 있고, 이 때 그 결과 쿼터니언이 특정 각도에서만 실패하는 이유를 알아내기 위해 많은 시간을 고민했습니다.
쿼티니언으로의 변환
이제 다른 표현법을 쿼터니언으로 변환하는 방법을 배워봅시다. 저는 샘플 프로그램에 있는 모든 변환들을 사용하지는 않지만 역운동학 등의 보다 진보된 용도로 쿼터니언 방향을 사용하려고 할 때 이것들이 필요할 것입니다.
회전축과 각도(Angle Axis)로부터 쿼터니언으로 변환
3D공간에서의 임의의 회전축을 도는 회전은 아래처럼 쿼터니언으로 변환됩니다.
회전축이 (ax, ay, az) 이고 (반드시 단위 벡터여야 함) 회전 각도를 theta (라디안)이면 w = cos(theta/2) x = ax * sin(theta/2) y = ay * sin(theta/2) z = az * sin(theta/2)이 됩니다.
우선 회전축이 정규화되어 있어야 합니다. 만약 정규화된 회전축 벡터의 길이가 0이라면 회전이 없는 것을 의미하므로 쿼터니언은 단위(identity) 쿼터니언으로 설정되어야 합니다.
오일러로부터 쿼터니언으로 변환
오일러로부터 쿼터니언으로의 변환은 회전순서가 올바르지 않으면 안 되기 때문에 조금더 힘듭니다. 임의축으로부터 3개의 좌표축을 분해하면 오일러 각을 3개의 독립적인 쿼터니언으로 변환해서 이 3개의 쿼터니언을 곱하면 최종 쿼터니언을 얻을 수 있습니다.
따라서 오일러 각 (a, b, c)으로 세개의 독립적인 쿼터니언을 만들수 있으며
Qx = [ cos(a/2), (sin(a/2), 0, 0)] Qy = [ cos(b/2), (0, sin(b/2), 0)] Qz = [ cos(c/2), (0, 0, sin(c/2))]
최종 쿼터니언은 Qx * Qy * Qz로 구할수 있습니다.
역자주 –이것은 오일러 회전 순서가 x->y->z의 순서인 경우에만 해당됩니다. 다른 순서로 된다면 Qx * Qy * Qz이 다르게 표현됩니다
데모 - 짐벌락 피하기
드디어 "어떻게 쿼터니언이 짐벌락을 피할수 있지?"에 대해서 모두가 기다렸던 궁금증에 대답할 때가 왔습니다.
기본적인 아이디어는
- 회전을 표현하는 데 쿼터니언을 사용한다.
- 현재 방향에서 새로운 방향으로 변경하기 위해 하나의 임시 쿼터니언을 생성한다.
- 임시 쿼터니언과 원래의 쿼터니언을 곱한다. 이렇게 하면 양쪽 모두의 회전을 합성한 새로운 방향이 얻어진다.
- 이 결과 쿼터니언을 행렬로 변환해서 평소처럼 행렬 곱을 사용한다.
우선, 저는 샘플 코드에 대해서는 어떠한 책임도 지지 않겠습니다. 이 코드는 난잡스러고 제대로 구성되어 있지도 않습니다. 이것은 쿼터니언 테스트할 때 제 프로그램에서 사용했던 쿼터니언 코드를 간략히 줄여놓은 버전일 뿐입니다. 따라서 코드에 대해서 크게 신경을 쓰지 않았다는 점만 기억해 주셨으면 좋겠습니다(돈받고 파는 코드가 아니니까요 ^^)
저는 2개의 실행 가능한 샘플을 준비했습니다. 첫번째 프로그램인CameraEuler.exe (http://www.gamedev.net/reference/programming/features/qpowers/CameraEuler.zip)는 오일러 각을 사용해서 카메라를 구현한 예입니다.
여러분이 주의깊게 봐야 할 부분은 main.cpp의 Main_Lopp 함수입니다.
여러분이 while 문에서 눈여겨 봐야할 곳은 다음과 같습니다.
- X축, Y축, Z축 각각의 회전을, 3개의 각도로 보관 유지 부분
- 키를 누르면 관련된 회전량을 조정하는 부분
- while 문에서, 3 개의 오일러 각도를 회전 행렬로 변환해서 그것을 최종 변환 행렬에 곱하는 부분
위/아래 화살표 키는 X축의 회전, 왼쪽/오른쪽 화살표 키는 Y축회전, Insert/PageUp 키는 Z축회전을 담당합니다.
이 프로그램은, 짐벌락을 일으킵니다. 여러분이 짐벌락 현상을 보고 싶으면, 요를 90도로 취하고 X축이나 Z축회전을 시도해 보십시오. 그리고 무슨일이 일어나는지 살펴보세요.
지금부터는 쿼터니언으로 짐벌락 문제를 해결한 프로그램을 살펴봅시다. 이 프로그램은CameraQuat.exe (http://www.gamedev.net/reference/programming/features/qpowers/CameraQuat.zip)이며 앞의 프로그램을 조금 변경한 프로그램입니다.
여러분이 while문에서 눈여겨봐야하는 곳은 다음과 같습니다.
- 카메라 방향을 쿼터니언으로 표현한 부분
- 키 입력으로부터 3개의 각도를 얻는 부분. 이 3개의 각도는 on/off 스윗치이며, 누적되지 않는 다는 것에 주의하십시오. 저는 while문에 이것들을 리셋했습니다. 물론 이것이 최선의 방법은 아닙니다. 그냥 신속히 처리하기 위해서 그랬을 뿐입니다.
- 3개의 각도를 임시 쿼터니언으로 변환하는 부분
- 임시 쿼터니언과 카메라 쿼터니언을 곱해서 합성한 방향을 얻는 부분. 곱 순서에 주의.
- 이렇게 해 얻은 카메라 회전을 최종 변환 행렬을 위해 회전축과 각도에 의한 표현으로 변환하는 부분.
키가 눌러졌을 때, 저는 키 입력에 대응하는 고유의 축에서의 작은 회전을 나타내는 임시 쿼터니언을 생성했습니다. 그리고 임시 쿼터니언과 카메라 쿼터니언을 곱했습니다. 이 4차원 공간에서의 회전을 합성한 것이 짐벌락을 피하게 해줍니다. 여러분이 직접 이것을 해보고 자신의 눈으로 확인해주세요.
카메라 쿼터니언은 최종 변환 행렬로 합성할 수 있도록 행렬이나 그에 상응하는 형태로 변환되야 합니다. 여러분이 쿼터니언을 사용할 때, 3차원 공간과 4차원 공간은 섞일 수가 없기 때문에 항상 이 작업을 해주셔야 합니다. OpenGL의 경우에 저는 그냥 쿼터니언으로부터 회전축을 변경하기만 했고 나머지는 API에게 위임했습니다.
제가 두번째 프로그램에서 오일러 각을 회전에 사용하지 않았지만 저는 여러분이 첫번째 프로그램에서의 오일러 회전에 대해서 볼 수 있게 하기 위해서 오일러 회전 부분을 남겨 두었습니다. 오일러 각은 하나 이상의 축으로 회전시키면 올바르게 되지 않을 것입니다. 왜냐하면 쿼터니언이 카메라 쿼터니언으로부터 오일러 각을 얻는 대신 키 입력을 통해서 계산하기 때문입니다. 두번째 프로그램은 프로그램을 시작했을 때 그냥 여러분이 요 값을 90도로 회전하려는 경우에 짐벌락이 더 이상 일어나지 않는다는 것을 보기 위해서 만든 참고자료일뿐입니다.
Note: 저는 여러분에게 저의 수학 라이브러리를 사용하라고 추천하고 싶지 않습니다. 여러분이 쿼터니언을 이해하고 나서 스스로 짜 보십시오. 참고로 저는 이 코드를 전부 버리고 다시 만들 예정입니다. 이 코드들은 저에게 있어서 너무나 지저분하고 난잡한 코드입니다.
제가 보여드리지 않은 것
여러분이 이미 눈치채셔겠지만 저는 쿼터니언을 오일러 각으로 변환하는 방법에 대해서는 설명하지 않았습니다. 그 이유는 아직까지도 완벽하게 동작하는 변환을 제가 알아내지 못했기 때문입니다. 제가 알고 있는 유일한 방법은 쿼터니언으로부터 행렬을 얻고, 그 행렬로부터 오일러 각을 추출하는 것입니다. 그러나, 오일러에서 행렬 변환은 다대일 관계(sin과 cos으로 인해)이기 때문에 저는 atan2를 사용해서 그 역을 구하는 방법을 알지 못합니다. 만약 정확하게 행렬로부터 오일러 각을 추출하는 방법을 알고 계시다면 저에게 알려주세요.
제가 보여드리지 않은 다른 내용은 행렬을 쿼터니언으로 변환하는 방법입니다. 여러분이 오일러 표현과 회전축과 각도에 의한 표현을 쿼터니언으로 변환할 때 행렬을 거치지 않고도 직접변환이 가능하므로 굳이 행렬을 쿼터니언으로 변환할 필요가 없기 때문입니다.
과제 - SLERP
여러분이 쿼터니언을 완전히 이해했다고 생각하신다면 다시 한번 생각해 보십시오. 아직도 쿼터니언에 대해서 더 배워야 할 게 남아 있습니다. 제가 전에 회전축과 각도(Axis Angle)에 의한 표현이 왜 나쁠까라고 말했던 것을 기억하시나요? '보간'이라는 단어가 갑자기 떠오르지 않나요?
저는 쿼터니언을 사용한 보간에 대해서 설명한 시간을 갖지 못했습니다. 이 글은 제가 예상한 것보다 시간이 오래 걸렸습니다. 여기서 SLERP(구면 선형 보간)에 대한 기본적인 아이디어를 드리겠습니다. 이것은 기본적으로 2개의 쿼터니언 방향 사이에 일련의 쿼터니언들을 생성합니다. 일련의 쿼터니언들은 처음과 마지막 쿼터니언사이에서 부드러운 모션(움직임)의 결과를 제공합니다. 오일러와 회전축 표현으로는 일관성있게 이러한 부드러운 움직임을 만들 수 없습니다.
마지막으로
저는 이 기사가 쿼터니언 이론 뒤에 숨겨진 알수 없는 미스테리들을 속시원하게 없애주었길 바랍니다. 다시한번 마지막으로 여러분에게 당부하고 싶은 말은 서로 다른 좌표계에서 2개의 쿼터니언을 곱하지 말아주십시오. 이렇게 하시면 여러분은 고통의 시간을 맛보시게 될것입니다.
그러면 새로 찾아낸 쿼터니언의 능력에 여러분이 기뻐하시길 바라면서 저는 이제 그만 여러분과 헤어질까 합니다. 몸조심하시구여. 그리구 다시 만나뵙기를 바라면서...
![]() Load 함수
Load 함수![]() fscanf 함수
fscanf 함수





















 관찰자의 시선방향을 따라가서 빛을 내보낸 물체를 찾아내는 방법이다. 시선이 물체에 닿았다는 것은 그 방향에서 물체의 빛이 눈으로 들어오는 것을 의미하므로, 시선방향으로 빛을 역추적하면 눈에 들어올 광선만을 추적할 수 있게 된다. 그러므로 광원에서 나오는 무한히 많은 빛들 중에서 눈에 들어올 빛을 찾아내는 정방향 광선추적법보다 시선방향으로 빛을 역추적하는 역방향 광선추적법이 훨씬 효율적임을 알 수 있다.
관찰자의 시선방향을 따라가서 빛을 내보낸 물체를 찾아내는 방법이다. 시선이 물체에 닿았다는 것은 그 방향에서 물체의 빛이 눈으로 들어오는 것을 의미하므로, 시선방향으로 빛을 역추적하면 눈에 들어올 광선만을 추적할 수 있게 된다. 그러므로 광원에서 나오는 무한히 많은 빛들 중에서 눈에 들어올 빛을 찾아내는 정방향 광선추적법보다 시선방향으로 빛을 역추적하는 역방향 광선추적법이 훨씬 효율적임을 알 수 있다.



























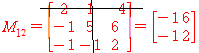
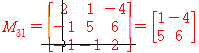
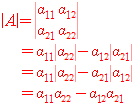
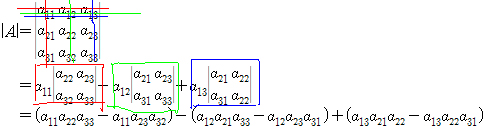
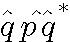 인 결과 즉 사원수3개의 곱으로(또는 p 가 w=0 인 벡터여도 상관없다) 나온 결과들을
인 결과 즉 사원수3개의 곱으로(또는 p 가 w=0 인 벡터여도 상관없다) 나온 결과들을 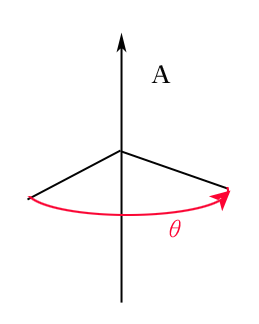






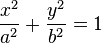
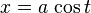
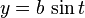


 이다.
이다.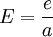 는 다음과 같이 정의된다.
는 다음과 같이 정의된다.