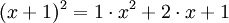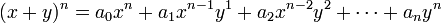베지어 곡선

 

http://kin.naver.com/open100/detail.nhn?d1id=11&dirId=1113&docId=234193&qb=67Kg7KeA7Ja0IOqzoeyEoA==&enc=utf8&section=kin&rank=2&search_sort=0&spq=0&pid=gkyGCz331yVssc%2B5Lg8ssv--496937&sid=Tby37L6VvE0AACnTDDU

 

1. 수학적으로 N차 베지어 곡선은 다음과 같이 정의된다.

 

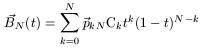
t가 0에서 1까지일때, 벡터 B_N이 그리는 궤적이 베지어 곡선이다.

벡터 p_k 는 조정점(control point)이고, N C k는 조합, N!/k!/(N-k)!을 의미한다.

 

어도브사에서 정한 ps 규약 중의 하나인 3차 베지어 곡선의 경우, 다음과 같이 요약할 수 있다.

 

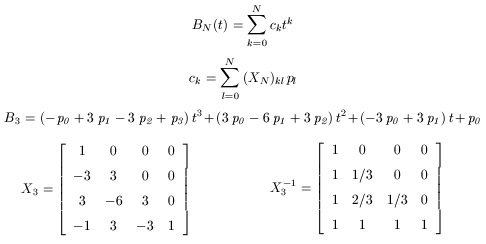
(편의상 B, p의 벡터 기호는 생략한 것임)

 

2. 베지어 곡선의 성질은 여러가지가 있는데, 대표적으로

 

1) 시작점:t=0일 때, p_0점

2) 끝점:t=1일 때, p_N점

3) 시작점에서 접선은 p_0, p_1의 변위와 평행

4) 끝점에서 접선은 p_N-1, p_N의 변위와 평행

5) 언제나 조정점들의 convex hull안에 들어간다.

6) 조정점들 중 여러 개를 같은 좌표로 설정하면, 그 부분에서 convex hull에 점점 가까워진다. 즉, 곡률이 더 심해진다.

 

3. 역사

수학적으로 예전에 알려진 곡선이지만, 피에르 베지어(Pierre Bézier)가 1960년대에 자동차 모델, 르노를 CAD로 디자인 할 때, 사용했는데, 그의 이름이 붙었다.

 

 

 

http://seirion.com/130

 

3차 베지어 커브 일반식 유도

혹자는 왜 하필이면 3차 베지어 커브이냐 ... 라고 궁금증을 가질 수도 있지만,
대부분의 폰트는 3차 이하의 베지어 커브들로 구성된다는 점,
3차 베지어 커브이면 원에 가까이 근사할 수 있다는 점 등이 그 이유일 것이다.
실제로 베지어 커브로는 완벽한 원을 만들 수 없다.

따지고 보면 1차 베지어 커브(사실은 직선)로도 원하는 모양을 만들 수 있긴 하다.
물론 이건 매우 비효율적이다. 어차피 픽셀로 표현되는 컴퓨터 나라에서 곡선이란 게 무의미 할 수도 있다.
아무튼 그건 그거고 ...

3차 베지어 커브의 일반식을 유도하기 위한 조건은 다음과 같다.
1. 컨트롤 포인트는 4개이다. (P0, P1, P2 and P3)
2. 곡선은 첫번째 포인트와 마지막 포인트를 지난다.
3. 곡선의 첫 지점에서의 기울기는 P0 과 P1 을 이은 직선의 기울기의 3배이다.
4. 곡선의 마지막 지점에서의 기울기는 P2 와 P3 을 이은 직선의 기울기의 3배이다.

 

*원본에 내용을 덧붙인다,

4. 곡선의 마지막 지점에서의 기울기는 P2 와 P3 을 이은 직선의 기울기의 3배이다.

 3배가 되는 이유는

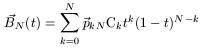
 에서 N=3, 일경우 이것은 3차 방정식형태로 전계되며 (1-t)^3 에 관한 계수들은

파스칼의 삼각형( 이항계수: n개 중에서 k개를 뽑을 수 있는 개수) 에 의하여 3이 곱해진다

2차일때 1,2,1 이 곱해지듯 전개되는 두번째와 세번째 항에 3에 곱해짐으로

이항계수는 다음과 같다.

{n \choose k} = \frac{n!}{k!(n-k)!} \quad \mbox{if } n\geq k\geq 0 \qquad \mbox{(1)}

{n \choose k} = 0 \quad \mbox{if } k<0 \mbox{ or } k>n


{n \choose k}    =nCk, C(n,k)

ex)  {7 \choose 3} = \frac{7\cdot 6 \cdot 5}{3\cdot 2\cdot 1} = 35

 

 

파스칼의 삼각형은 수학에서 이항계수를 삼각형 모양의 기하학적 형태로 배열한 것이다. 이것은 블레즈 파스칼에 의해 이름 붙여졌으나 이미 수세기 전에 다른 사람들에게서 연구된 것이다.


Pascal triangle.svg

 

 

파스칼 삼각형의 응용

파스칼의 삼각형은 이항 전개에서 계수들의 값을 계산하는 데에 사용된다. 예를 들어

(x + 1)^2 = 1 \cdot x^2 + 2 \cdot x + 1

라는 식에서, 각 계수의 값인 1, 2, 1은 파스칼의 삼각형의 3번째 줄에 대응된다.

일반적으로,

(x + y)^n = a_0 x^n + a_1 x^{n-1} y^1 + a_2 x^{n-2} y^2 + \cdots + a_n y^n

와 같은 전개식에서, a_i = {n \choose i} 가 성립한다. 즉, ai는 파스칼의 삼각형의 (n+1) 번째

줄의 (i+1) 번째 값과 대응된다.

 

 

 

 

위 사실에 근거하여,
3차 식을 다음과 같이 u에 대한 3차 식으로 두고,

사용자 삽입 이미지






이놈을 매트릭스로 표현하면,

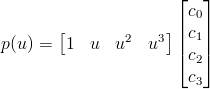
사용자 삽입 이미지







즉, 

사용자 삽입 이미지






그리고 미분한 식은 다음과 같다.

사용자 삽입 이미지






위 조건 1,2,3,4 를 적용하여 보면,

[식 1.1]

사용자 삽입 이미지



 

사용자 삽입 이미지



 

사용자 삽입 이미지



 

사용자 삽입 이미지






 

사용자 삽입 이미지

이 식에서 

사용자 삽입 이미지

로 치환하면, 다음과 같다.

사용자 삽입 이미지




조건 1,2,3,4 로부터 유도된 식으로부터 

사용자 삽입 이미지


 

사용자 삽입 이미지

를 구할 수 있고, 값은 다음과 같다.

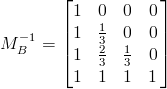
사용자 삽입 이미지
사용자 삽입 이미지






 

*원본에 덧붙인다.
결론적으로 ([계수행렬][t])^T * [P] 로써 베지어 곡선이 표현되며,

계수 행렬을 구하면 핵심적인 것이 정리된다,

이 계수 행렬은 [식 1.1] 들의 P 들로 풀이되는Pn 들을 P0~3 까지 서로 연립하여 풀면 Pn 들에 붙는

 Mb 같은 계수행렬 형태로 정리할 수 있게 된다

한가지 힌트는 Mb 행렬중 가장 오른쪽 열이 P0에 대하여 풀어 나온 나온 계수가 된다.

마찬가지로 3 열이 P0 의 계수는 -3, P1 의 계수는 3 이다.


 

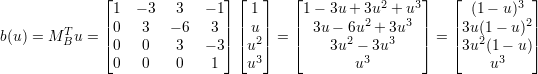
사용자 삽입 이미지

라고 치환하면,

사용자 삽입 이미지

이렇게 되고, 

고로, 

사용자 삽입 이미지

다음을 통해서 b(u) 를 구할 수 있다.


*원본에 덧붙인다.

결과적으로 계수행렬  Mb^T 와 U 를 곱하여  (1-t)^3 즉 3차에 관한 항들로 전계가 되고

이것이 P 와 곱해짐으로써 베지어 곡선을 만들 수 있게 된다.

Tip : 3차식=3차곡선= N=4= N-1 곡선,  점이 4개면 3차 곡선 형태가 된다





이제 다 끝났다.

사용자 삽입 이미지



이었으므로, 다음과 같은 일반항이 도출된다.

사용자 삽입 이미지








references : 
http://en.wikipedia.org/wiki/B%C3%A9zier_curve
Interactive Computer Graphics 2nd Edition (Addison Wesley) p434-436

 

 

 

Bézier curves


Written by Paul Bourke
Original: April 1989, Updated: December 1996

 

이 문서는 베지어 곡선이라는 특수한 곡선에 대한 수학적인 설명을 담고 있습니다. 이 곡선의 이름은, 1970년대 Renault car를 디자인하는 과정에서 이 곡선을 사용했던 Pierre Bézier라는 프랑스 엔지니어의 이름을 따서 만들어졌습니다. 그때부터 이 곡선은 식자 산업(typesetting industry)에서 절대적인 우위를 점하게 되었고, 특히 Adobe Postscript, 폰트 제품 등에서 널리 사용되었습니다.

3차원 공간에 있는 N+1개의 조절점(control point) pk (k=0,1,...,N)를 생각해봅시다. 베지어 parametric 곡선 공식은 다음과 같습니다.

B(u)는 서로 다른 위치에 있는(discrete) N개의 조절점에 의해 얻어지는 곡선을 구하기 위한 연속함수입니다. u=0이면 첫번째 조절점(k=0)에, u=1이면 마지막 조절점(k=N)에 도달합니다. 아래는 N=4, 즉 조절점이 4개인 경우의 곡선 모습입니다.
역자 주 : 첫번째 조절점이 시작점, 마지막 조절점이 끝점이라고 생각하시면 쉽겠죠? ^_^ 
그리고, N개의 조절점이 아니라 N+1의 조절점이라고 해야 하는 듯. 
나중에 나오지만, 조절점의 위치가 모두 각각 다를 필요는 없습니다.

주의점:

  • 이 베지어 곡선은, 조절점 중 처음과 끝 점을 빼고는 보통 어느 조절점과도 만나지 않습니다. 공식을 사용하면 B(0) = P0 이고 B(1) = PN 이 되겠지요.

  • 곡선은, 항상 조절점으로 이루어진 다각형 안에 들어가게 됩니다. 곡선이 조절점들 사이에서 크게 벗어나거나 하는 일은 없습니다.

  • 조절점이 P0 하나뿐이라면, 즉 N=0 이라면 모든 u에 대해 B(u) = P0 입니다. (역자 주 : u는 0이상 1 이하의 실수)

  • 조절점이 P0 , P1 두개뿐이라면, 즉 N=1이라면 이 공식은 두 점 사이를 잇는 선분을 만들어냅니다.


  • 라는 부분은 blending 함수라고 하는데, 이 부분에서 조절점들을 blend해서 곡선을 생성하기 때문입니다.

  • blending 함수는 조절점의 갯수보다 차수가 하나 낮은 다항함수입니다. 예를 들어, 3개의 조절점이 있다면 베지어 곡선은 포물선을 그리고, 4개의 조절점으로는 3차곡선을 얻게 됩니다.

  • 첫번째 조절점의 위치와 마지막 조절점의 위치가 같을 경우 폐곡선이 생깁니다. 이때 처음의 두 조절점 사이의 접선(tangent)과 끝의 두 조절점의 접선이 같을 경우, first order continuity가 가능합니다. (역자 주 : P0 - P1 간의 기울기와 PN-1 - PN 간의 기울기가 같을 경우..라고 보시면 되겠습니다. first order continuity는, 두 곡선의 (1계)도함수가 같은, 즉 접선의 기울기가 서로 같은 상태를 의미합니다.) 

  • 비슷한 위치에 여러 조절점이 있을 경우, 그쪽으로 베지어 곡선을 "당기는" 정도가 증가합니다.

  • 조절점의 갯수가 많아지면, 좀더 높은 차수의 식과, 많은 횟수의 팩토리얼 값을 계산해야 합니다. 그래서 보통 긴 곡선을 만들 때는, 그 곡선을 다시 여러 곡선으로 작게 쪼개는 방법을 씁니다. 이렇게 하면, 전체적인 모습에 변화를 주지 않고도 곡선의 부분적인 형태를 쉽게 바꿀 수 있는 효과도 얻게 됩니다. 물론 곡선이 첫번째 조절점에서 시작해서 마지막 조절점에서 끝나기 때문에, (나눠진) 곡선 조각들을 이어붙이기는 쉽습니다. 또한 베지어 곡선에서는 마지막 점에서의 접선이 마지막 두 조절점을 이은 선과 같기 때문에, (나누어진 곡선들의) 첫번째 조절점의 기울기도 맞출 수 있습니다. 
    Second order continuity는 보통 불가능합니다. (역자 주 : Second order continuity는, 이계도함수의 값이 같을 때의 상태입니다. 즉, 곡선의 변화율이 같다는 뜻입니다.) 

  • 조절점이 2개인 특수한 경우(직선)을 제외하고는, 한 베지어 곡선에 평행한 다른 베지어 곡선을 유도(derive)해내는 것은 불가능한 것으로 알려져 있습니다.

  • 베지어 곡선으로 원을 완벽하게 표현할 수는 없습니다.

  • coincident parallel curves나 직선인 베지어 곡선의 경우를 제외하고는, 한 베지어 곡선에 평행한 베지어 곡선을 만드는 것은 불가능합니다.

  • 조절점이 3개일 경우는 공식이 다음과 같이 정리됩니다 : 

    B(u) = P0 * ( 1 - u ) 2 + P1 * 2 * u ( 1 - u ) + P2 u2

  • 조절점이 4개일 경우는 공식이 다음과 같이 정리됩니다 : 

    B(u) = P0 * ( 1 - u )3 + P1 * 3 * u * ( 1 - u )2 + P2 * 3 * u2 * ( 1 - u ) + P3 * u3

베지어 곡선은 굉장히 안정적인 형태를 만들고, 계산하기도 쉽기 때문에 널리 쓰이고 있습니다. 이런 형태의 베지어 곡선 말고도 조금 다른 모습을 만들어 내는, 또다른 베지어 곡선 공식이 있습니다. 대체로 모습은 비슷하지만, 곡선이 각 조절점을 모두 통과한다는 점이 다릅니다. Spline 곡선을 참조하세요.

예제

분홍색 선이 조절점들을 이은 선이고, 회색 선이 베지어 곡선입니다.

베지어 곡선을 표현하는 다항식의 차수는 조절점의 갯수보다 하나 낮기 때문에, 조절점이 세 개인 이 경우에는 2차곡선이 만들어집니다. 두 곡선의 조절점의 모양이 대칭을 이루면, 곡선 또한 항상 대칭입니다.

곡선은 항상 끝점을 지나며, 처음의 두 점을 이은 선에 접하고 끝의 두 점을 이은 선에도 접합니다. 이 성질로 인해, first order continuity를 유지하면서 여러 베지어 곡선을 이을 수 있게 됩니다.

곡선은 항상 조절점들로 이루어진 볼록다각형(convex hull) 안에 있게 됩니다. 그래서 곡선은 "안정적이고", 엉뚱하게 튀어나가는 일이 없습니다.

시작점과 끝점을 갖게 했을때 곡선이 생깁니다. 시작점과 끝점의 접선(tangents)이 일치할 경우 곡선은 first order continuity를 유지하면서 닫히게 됩니다. 또, 조절점을 한 곳에 여러번 지정하게 되면, 그 쪽으로 곡선이 쏠리게 됩니다.

C source

typedef struct XYZ

{

    double x;

    double y;

    double z;

}XYZ;

/*

조절점이 3개인 베지어 곡선 예제

mu는 0(곡선의 시작)부터 1(곡선의 끝) 사이의 값을 가질 수 있습니다.

*/

XYZ Bezier3(XYZ p1,XYZ p2,XYZ p3,double mu)

{

    double mum1,mum12,mu2;

    XYZ p;

    mu2 = mu * mu;

    mum1 = 1 - mu;

    mum12 = mum1 * mum1;

    p.x = p1.x * mum12 + 2 * p2.x * mum1 * mu + p3.x * mu2;

    p.y = p1.y * mum12 + 2 * p2.y * mum1 * mu + p3.y * mu2;

    p.z = p1.z * mum12 + 2 * p2.z * mum1 * mu + p3.z * mu2;

    return(p);

}

/*

조절점이 4개인 베지어 곡선 예제

mu는 0(곡선의 시작)부터 1(곡선의 끝) 사이의 값을 가질 수 있습니다.

*/

XYZ Bezier4(XYZ p1,XYZ p2,XYZ p3,XYZ p4,double mu)

{

    double mum1,mum13,mu3;

    XYZ p;

    mum1 = 1 - mu;

    mum13 = mum1 * mum1 * mum1;

    mu3 = mu * mu * mu;

    p.x = mum13*p1.x + 3*mu*mum1*mum1*p2.x + 3*mu*mu*mum1*p3.x + mu3*p4.x;

    p.y = mum13*p1.y + 3*mu*mum1*mum1*p2.y + 3*mu*mu*mum1*p3.y + mu3*p4.y;

    p.z = mum13*p1.z + 3*mu*mum1*mum1*p2.z + 3*mu*mu*mum1*p3.z + mu3*p4.z;

    return(p);

}

/*

일반적인 베지어 곡선 예제

조절점의 갯수는 n+1개가 됩니다.

0 <= mu < 1 *중요!* 마지막 조절점은 계산하지 않습니다.

*/

XYZ Bezier(XYZ *p,int n,double mu)

{

    int k,kn,nn,nkn;

    double blend,muk,munk;

    XYZ b = {0.0,0.0,0.0};

    muk = 1;

    munk = pow(1-mu,(double)n);

    for (k=0;k<=n;k++)

    {

        nn = n;

        kn = k;

        nkn = n - k;

        blend = muk * munk;

        muk *= mu;

        munk /= (1-mu);

        while (nn >= 1) {

            blend *= nn;

            nn--;

            if (kn > 1) {

                blend /= (double)kn;

            kn--;

            }

            if (nkn > 1) {

                blend /= (double)nkn;

                nkn--;

            }

        }

        b.x += p[k].x * blend;

        b.y += p[k].y * blend;

        b.z += p[k].z * blend;

    }

    return(b);

}

  • FAQ
    > 1. SpLines 코드 - 코드를 이해하기 위한, 간단한 테스트
> 프로그램이 있습니다. 정말 괜찮게 구현해놓았네요. 질문이 하나 있습니다:
> 어떻게 동적인 결과(dynamic resolution)를 얻을 수 있을까요?
> 2. Bezier 코드에서 - 어떻게 이 코드를 쓰는지에 대한 예제가 없네요.. 
> 세 함수 모두 곡선을 만드는 대신, 단지 점 하나만을 리턴하네요. 
> 게다가 double형 인자인 mu( 0 < mu <1) 는 뭐죠?

함수를 호출할 때는, 0부터 1 사이의 범위에서 mu값을 바꾸면서 함수들을
호출하세요. mu의 값을 증가시킴에 따라, 곡선 위에서 (곡선 방향으로) 이동하는 
점들을 얻게 됩니다. 그러므로 mu에 0.5를 넣는다면, 전체 곡선(길이)의 딱 중간에
있는 점을 함수가 리턴하겠지요. 하나 예를 들어볼게요.

   #define NSTEPS 100
   int ncontrolpoints=0;
   XYZ p,*controlpoints;
   
   ... 이곳에 조절점 배열과, 데이터들을 만들고 읽는 루틴이 들어가겠지요.

   for (i=0;i%lt;NSTEPS;i++) {
      p = Bezier(controlpoints,ncontrolpoints,i/(double)N));

      .... 이제 p 변수를 이용하세요. 예를 들어, 화면에 찍는다거나 등등.

   }

spline 코드가 호출되는 방식도, 이와 같습니다.
출처 : http://eunchul.com/Algorithms/BezierCurves/BezierCurves.htm
 
 
 
베지어 곡선뒤에 숨겨진 수학원리 #
좋습니다. 가장먼저 짚고 넘어가야할 것은 번스타인(Bernstein) 정리 공식"들"입니다. 자, 이제 공식하나를 보여줄 예정인데, 초조해할 필요는 없습니다. 단지 이 공식을 보면 정말로 간단하다는 것을 금방 알 수 있을거니까요.
1 = t + (1 - t)

t는 어떠한 상수라도 될 수 있으며 이 공식은 모든 경우의 수에 대하여 언제나 참입니다. 그러나 이 아티클에서는 t가 0과 1사이일 경우만 고려하도록 하겠습니다.

이제 번스타인 정리 공식을 알았습니다. 그러나 이전에 제가 공식"들"이라고 복수형으로 말했던 것을 기억하세요! 자, 잘 동작하는 곡선을 얻기위한 다음 단계는 우리의 자그마한 데모에서 어떤 종류의 곡선을 사용할 것인지 선택하는 것입니다. 초심자를 위해서, 여기서는 가장 쉬운 형태인 2차 베지어 곡선을 사용하도록 하겠습니다.

자, 그리하여 2차 베지어 곡선을 택하게 되었습니다. 이제 전지전능한 정리 공식으로부터 몇가지 공식들을 끌어내야할 필요가 있습니다. 2차 베지어 곡선을 위해서는, 우선 번스타인 정리 공식의 양변을 제곱합니다. 3차 베지어 곡선을 얻으려면, 양변을 3제곱합니다. 그 이상의 차수에도 마찬가지입니다. 양변을 제곱하면 다음과 같은 결과가 나올겁니다.
1^2 = (t + (1 - t))^2
1 = t^2 + 2*t*(1-t) + (1-t)*(1-t)


You'll notice that a lot of this I didn't simplify, that's because it's easier to understand and code if you leave it this way.

Ok, now we have our 3 functions, which we derived from our basis. But where you ask. Well, right in front of you! Our functions are each of the terms to the right side of the equation. We'll call our functions Bx(t). It should be noted that the code is in bold.

#define	B1(t)		(t*t)
#define	B2(t)		(2*t*(1-t))
#define	B3(t)		((1-t)*(1-t))

2차 베지어 곡선인 경우에는 위 3개의 공식만 알고 있으면 됩니다.

참고로 3차(cubic) 곡선인 경우는 아래와 같습니다.
B1(t) = t * t * t
B2(t) = 3 * t * t * (1 - t)
B3(t) = 3 * t * (1 - t) * (1 - t)
B4(t) = (1 - t) * (1 - t) * (1 - t)


4차(quartic) 곡선인 경우입니다.
B1(t) = t * t * t * t
B2(t) = 4 * t * t * t * (1 - t)
B3(t) = 6 * t * t * (1 - t) * (1 - t)
B4(t) = 4 * t * (1 - x) * (1 - t) * (1 - t)
B5(t) = (1 - t) * (1 - t) * (1 - t) * (1 - t)


이렇게 분해해놓은 공식만있으면 수학공식정리를 하지 않아도 됩니다! 이제 베지어 곡선뒤에 숨은 간단한 수학을 건너뛰었습니다. 이들을 가지고 프로그램을 논하도록 하죠!
베지어 곡선
번스타인(Bernstein) 정리 공식들 
1 = t + ( 1 - t ) 
▒ 0 ≤ t ≤ 1 
2차 베지어 곡선이라면 양변에 제곱 
3차 베지어 곡선이라면 양변에 세제곱 
... 
2차 베지어 곡선 
1^2 = t^2 + 2 * t * ( 1 - t) + ( 1 - t ) * ( 1 - t )
3차(cubic) 베지어 곡선 
1^3 = t * t * t + 3 * t * t * (1 - t) + 3 * t * (1 - t) * (1 - t) + (1 - t) * (1 - t) * (1 - t)
4차(quartic) 베지어 곡선 
1^4 = t * t * t * t + 4 * t * t * t * (1 - t) + 6 * t * t * (1 - t) * (1 - t) + 4 * t * (1 - x) * (1 - t) * (1 - t) + (1 - t) * (1 - t) * (1 - t) * (1 - t)
제어점은 각 식에 대해서 곱의 합으로 분리했을때 곱의 갯수이고 
각 제어점들을 각 곱에 곱해줌으로써 값들은 베지어 곡선을 이루게 된다. 
2차 베지어 곡선의 예제 코드 
public double B1(double t) 
{ 
    return t*t; 
} 
public double B2(double t) 
{ 
    return 2 * t * (1 - t); 
} 
public double B3(double t) 
{ 
    return (1 - t) * (1 - t); 
} 
... 
    double x, y; 
    double detailBias = 1.0 / 50.0; 
    double count = 0; 
    do 
    { 
      x = pt0].X * B1(count) + pt[1?.X * B2(count) + pt[2].X * B3(count); 
      y = pt0].Y * B1(count) + pt[1?.Y * B2(count) + pt[2].Y * B3(count); 
      image.SetPixel?((int)x, (int)y, Color.Black); 
      count += detailBias; 
    } while (count <= 1); 
출처 : http://www.synch3d.com/wiki/moin/moin.cgi/_ba_a3_c1_f6_be_ee_20_b0_ee_bc_b1

                    
        

  

    
반응형

    
    
    
  



        







                    

  



  



  



            

                
                    
                        저작자표시 비영리 동일조건 
                    
                
            

              




                    


  
'수학 (Mathematics) > 3D수학' 카테고리의 다른 글

  

    

      [2D] 두 선분의 교차판정  (0)
      2012.11.02
    

    

      NDC 공간이란  (0)
      2012.11.02
    

    

      3차 곡선, 에르미트 곡선 도출에서 근사적 좌표프레임까지 얻어내기  (0)
      2012.11.02
    

    

      두 벡터 사이의 각  (0)
      2012.11.02
    

    

      벡터 미적분, 접선과 가속도 - 공간 곡선  (0)
      2012.11.02
    

  






	


	

	




                 
             

			

			

			
			


			
			

				
+ Recent posts

				
    
					
					
    
				

			

			

			


			
		
 
	
 

 









  
티스토리툴바