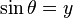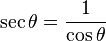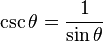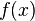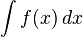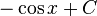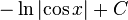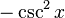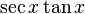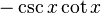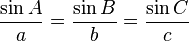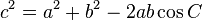곱을 합차로...
아래 공식은 삼각함수의 합공식에서부터 유도되어 진다
sin(a)cos(b)=1/2[sin(a+b) + sin(a-b)]
cos(a)sin(b)=1/2[sin(a+b) - sin(a-b)]
다를때는 sin
cos(a)cos(b)=1/2[cos(a+b) + cos(a-b)]
sin(a)sin(b) =1/2[cos(a+b) - cos(a-b)]
같을때는 cos
차수를 낮추는 삼각함수
sin^2(x)=(1-cos(2x))/2
cos^2(x)=(1+cos(2x))/2
sin(x)cos(x) = (sin(2x))/2
이때 주의해서 봐야 할 것은 원래의 각도에서 2배 만큼 올려준다는 것!!
ex) sin 과 cos 가 엮였을때의 적분법!!!!!
두개의 삼각함수중 하나가 홀수 승이고 하나가 짝수 승일때는 또는 둘다 홀 수 승일때
(홀수승일때 3 이상 일때 ), 그 이하일때는 바로 d 에 넣어버리면 된다
홀수승의 차수를 하나 낮추어서 분리한 후
분리한 것을 d 속에 적분하여 넣고
d(적분해 넣은것) 을 기준으로 적분을 하는데
적분하게될 변수에 맞춰 짝수였던 삼각 함수를 적변 변수에 맞게
1-cos^2 형태 또는 1-sin^2 형태로 변형하여 적분을 한다
삼각 함수가 짝수. 짝수 승일때의 적분은
차수를 낮추는 삼각함수를 이용하여 적분 할 수 있을때까지 차수를 낮추는 삼각 함수를 계속 대입한다
삼각함수와 대수 함수가 결합된 형태라면 부분적분을 이용하는데
그때 대수 함수를 미분형태가 되는 전개로 봐야 계산전개가 편하다
대수함수를 계속 미분하다보면 대부분 0 으로 떨어지는 항이 나타난다
-승 인상황은 주의.
이하부터는 첨부내용
삼각함수
삼각함수(三角函數,Trigonometric functions)는 수학에서 사용되는 각에 대한 함수이다. 삼각함수는 삼각형이나 주기적 현상의 가정에 주로 사용된다. 삼각함수는 일반적으로 해당 각이 존재하는 직각삼각형의 두 변의 비로 정의되며, 단위원에서의 가변적인 호의 길이의 비로 정의되기도 한다. 이들은 무한급수나 특정 미분방정식의 해로도 표현되어, 그 영역이 임의의 양의 값과 음의값, 또는 복소수로 확장되기도 한다. 삼각함수에는 6개의 기본 함수가 있다.
삼각함수는 삼각형의 각에 변을 연관시킬 때 사용된다. 삼각함수는 여러 방면에 응용되고 있으나, 특히 삼각형의 연구나 주기적 현상의 모형 구축에 중요하게 쓰인다.
목차[숨기기] |
[편집]기하학적 정의
각 C가 직각인 삼각형 ABC에서, 각 A, B, C의 대변(마주보는 변)의 길이를 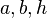 라고 할 때, 사인(sine), 코사인(cosine), 탄젠트(tangent)의 정의는 다음과 같다.
라고 할 때, 사인(sine), 코사인(cosine), 탄젠트(tangent)의 정의는 다음과 같다.
- 사인:
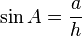
- 코사인:

- 탄젠트:

또한, 코시컨트(cosecant), 시컨트(secant), 코탄젠트(cotangent)는 위 세 함수의 역수가 되며, 다음과 같이 정의한다.
- 코시컨트:

- 시컨트:

- 코탄젠트:

 |  | 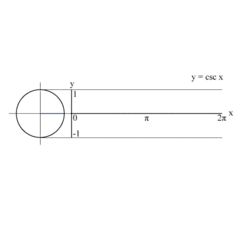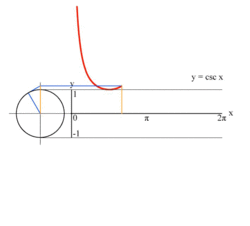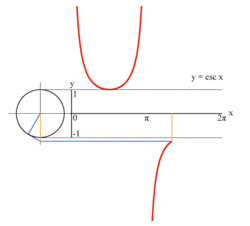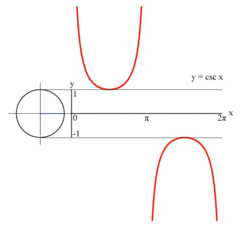 | ||
| 사인과 코사인의 그래프 | 탄젠트 그래프 | 코시컨트 그래프 |
[편집]단위원 정의
좌표평면에서 원점을 중심으로 하고 반지름의 길이가 1인 원을 단위원이라고 한다. 이 단위원 위의 점  에 대해, x축과 점과 원점을 잇는 직선간의 각을
에 대해, x축과 점과 원점을 잇는 직선간의 각을  라디안이라고 하면, 이때 사인, 코사인은 다음과 같이 정의된다.
라디안이라고 하면, 이때 사인, 코사인은 다음과 같이 정의된다.
또한, 나머지 함수들을 다음과 같이 정의한다.
이들은 주기함수로서, 각각  (사인/코시컨트, 코사인/시컨트)또는
(사인/코시컨트, 코사인/시컨트)또는  (탄젠트/코탄젠트)의 주기를 갖는다.
(탄젠트/코탄젠트)의 주기를 갖는다.
[편집]부호 및 변환표
각 사분면에 따른 삼각함수의 부호는 다음과 같다.
| 사분면 | sin과 csc | cos과 sec | tan와 cot |
|---|---|---|---|
| I | + | + | + |
| II | + | − | − |
| III | − | − | + |
| IV | − | + | − |
변환된 값은 다음과 같다.
| sin | cos | tan | cot | sec | csc | |
|---|---|---|---|---|---|---|
| sin(x) |  | 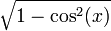 |  |  | 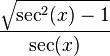 |  |
| cos(x) |  | 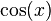 |  | 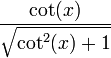 | 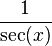 |  |
| tan(x) |  | 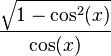 |  | 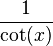 | 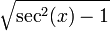 |  |
| cot(x) | 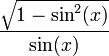 |  |  |  | 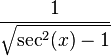 |  |
| sec(x) | 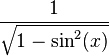 |  |  | 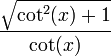 |  | 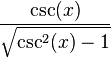 |
| csc(x) | 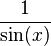 |  |  |  | 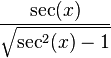 |  |
[편집]삼각함수 항등식
 이 부분의 본문은 삼각함수 항등식입니다.
이 부분의 본문은 삼각함수 항등식입니다.
삼각함수 사이에는 많은 항등식이 존재한다. 그 중 가장 자주 쓰이는 것은 피타고라스 항등식으로, 어떤 각에 대해서도 사인의 제곱과 코사인의 제곱의 합은 1이다. 이는 반지름의 길이가 r이고 밑변이 b, 각 x의 대변 a에 대하여  를 만족한다는 피타고라스의 정리로 설명할 수 있다. 이를 삼각함수로 나타내면 다음과 같다.
를 만족한다는 피타고라스의 정리로 설명할 수 있다. 이를 삼각함수로 나타내면 다음과 같다.
다른 삼각함수의 관계는 삼각함수의 덧셈정리이다. 두 각의 합과 차의 사인과 코사인은 x, y에 대한 사인과 코사인으로 구할 수 있다. 이는 제이 코사인 법칙과 두 점 사이의 거리 공식을 연립해 유도할 수 있고, 제일 코사인 법칙과 사인 법칙을 연립해 유도할 수 있고, 오일러의 공식을 이용해 유도할 수도 있다.

 (복부호 동순)
(복부호 동순)
두 각의 크기가 같을 경우에는 덧셈정리를 간단하게 배각공식을 이용할 수 있다.
[편집]미분과 적분
다음은 6개의 기본 삼각함수에 대한 도함수와 부정적분이다.
[편집]삼각함수의 성질과 응용
[편집]사인법칙
사인법칙은 임의의 삼각형 ABC에서 각 A, B, C의 대변 a, b, c에 대해 다음과 같은 관계를 만족함을 나타낸다.
마찬가지로,
도 성립한다. 여기서 R은 삼각형의 외접원의 반지름의 길이를 나타낸다.
[편집]코사인법칙
 이 부분의 본문은 코사인법칙입니다.
이 부분의 본문은 코사인법칙입니다.
가 성립하고, 위의 식을 변형하면
와 같이 나타낼 수 있다.
코사인법칙은 두 변의 길이와 끼인각의 크기를 알 때 삼각형의 나머지 한 변의 길이를 구할 때 유용하게 쓸 수 있다. 또한 모든 변의 길이를 알고 있을 때 각의 코사인값을 구할 때에도 사용할 수 있다.
[편집]순허수
오일러의 공식 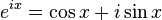 에
에
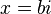 를 대입하면,
를 대입하면,
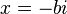 를 대입하면,
를 대입하면,
연립하여 풀면,
'수학 (Mathematics) > 미적분학' 카테고리의 다른 글
| 정적분 삼각치환 (0) | 2012.11.03 |
|---|---|
| 넓이를 구할때 사용되는 특수한 공식 (0) | 2012.11.03 |
| 적분법 (0) | 2012.11.03 |
| 적분법 (0) | 2012.11.03 |
| 부분적분법 공식 (0) | 2012.11.03 |