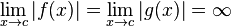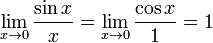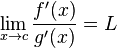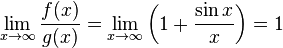로피탈의 정리

2012. 11. 2. 21:00

http://ko.wikipedia.org/wiki/%EB%A1%9C%ED%94%BC%ED%83%88%EC%9D%98_%EC%A0%95%EB%A6%AC

먼저 정리를 하자면 0/0, ∞/∞ 꼴에서 로피탈의 정리 사용이 가능한데

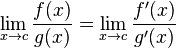
$&#-0; \lim_{x\to c}{f(x) \over g(x)} = \lim_{x\to c}{f'(x) \over g'(x)} &#-0;$

에서 g(x)≠0 이어야 하고 f', g' 후에도 f'(x)/g'(x) 에 극한값이 존재 해야 한다

그러나 한번 미분 후 0/0, ∞/∞ 꼴이 반복된다면 이러한 꼴이 나타나지 않을때까지

계속 반복을 해주어 극한값을 찾아낸다

$&#-0; \lim_{x\to c}{f'(x) \over g'(x)} = A, A \in \mathbb{R}^*&#-0;$
의 값 A가 확장된 실수상에서 존재하면, 아래의 극한값은 A와 같다.
$&#-0; \lim_{x\to c}{f(x) \over g(x)} = \lim_{x\to c}{f'(x) \over g'(x)} &#-0;$

[but]
복소함수에의 적용 불가
무한대 근처에서의 진동할 때의 적용 불가

로피탈의 정리(l'Hôpital's rule, 또는 l'Hospital's rule)은 해석학 및 미적분학에서 사용되는 함수의 극한에 관한 정리의 하나이다. 함수의 도함수를 사용하여, 부정형(不定形)의 극한값을 계산하는 데 이용된다.

이 정리의 이름은 17세기에 활동하였던 프랑스의 수학자이자 후작인 기욤 드 로피탈(Guillaume de l'Hôpital)의 이름에서 유래되었다. 로피탈은 그의 저서인 《곡선을 이해하기 위한 무한소 해석》(l'Analyse des Infiniment Petits pour l'Intelligence des Lignes Courbes)에서 이 정리를 소개하였다.

이 정리는 베르누이의 규칙(Bernoulli's rule)이라는 이름으로 불리기도 한다.^[1]

엄밀한 표현 [편집]

확장된 실수 $\mathbb{R}^*$ 상의 구간 $[a, b]$ 에서 연속이고 $(a, b)$ 에서 미분가능한 함수 $f (x)$ , $g (x)$ 가 있다. $c \in \mathbb{R}^*$ 라 하고, 이때 아래의 함수 $f$ , $g$ 의 c로의 극한의 값이 0이거나

$\lim_{x \rightarrow c} f(x) = \lim_{x \rightarrow c} g(x) = 0$

모두 발산하고

$\lim_{x\to c}{|f(x)|} = \lim_{x\to c}{|g(x)|} = \infty$

아래의 극한

$&#-0; \lim_{x\to c}{f'(x) \over g'(x)} = A, A \in \mathbb{R}^*&#-0;$

의 값 A가 확장된 실수상에서 존재하면, 아래의 극한값은 A와 같다.

$&#-0; \lim_{x\to c}{f(x) \over g(x)} = \lim_{x\to c}{f'(x) \over g'(x)} &#-0;$

예제 [편집]

좀 더 기술적인 계산에 대해서는 en:L'Hôpital's rule#Examples 문서를 참고하십시오.

예를 들어, 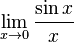$\lim_{x \to 0}\frac{\sin x}{x}$ 의 값은 다음과 같이 구할 수 있다.

$\lim_{x \to 0}\frac{\sin x}{x} = \lim_{x \to 0}\frac{\cos x}{1} = 1$

극한 존재의 필요성 [편집]

다음 극한이 존재한다는 조건이 필수적이다.

$&#-0; \lim_{x\to c}{f'(x) \over g'(x)} = L&#-0;$

미분된 함수의 극한이 존재하지 않을 경우 로피탈의 정리를 적용할 수 없는 경우도 있다. 예를 들어, $f(x) = x + \sin x, \;g(x) = x$ 일 경우,

$\lim_{x\to \infty} {f'(x) \over g'(x)} = \lim_{x\to \infty} {{1 + \cos x} \over 1}$

의 값은 존재하지 않지만, 다음 극한은 존재한다.

$\lim_{x\to\infty}\frac{f(x)}{g(x)} = \lim_{x\to\infty}\left(1+\frac{\sin x}{x}\right) = 1$

복소함수에의 적용 불가

무한대 근처에서의 진동할 때의 적용 불가

저작자표시 비영리 동일조건

'수학 (Mathematics) > 고,중학 수학 및 개념' 카테고리의 다른 글

부정적분 : 적분상수의 역습 (0)	2012.11.02
분수함수 미분 - 곱의 미분법으로 (0)	2012.11.02
극한값 , 발산 (0)	2012.11.02
자연대수 e 그래프 그리기 [영상강의] (0)	2012.11.02
이차함수, 그래프 (0)	2012.11.02

3DMP