이차함수, 그래프

2012. 11. 2. 20:58

이차 함수

위키백과 ― 우리 모두의 백과사전.

이동: 둘러보기, 찾기

이차 함수(Quadratic function)는 함수의 최고차항의 차수가 2인 함수를 말한다. 이차 함수의 일반형은 다음과 같다.

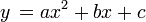$y\,=ax^2+bx+c$ (단, $a \ne 0$ )

또한 다음과 같은 형태를 이차 함수의 표준형이라 한다.

$y\,=a(x-p)^2+q$ (단, $a \ne 0$ )

x절편을 보다 쉽게 알아보기 위해서 다음과 같은 형태를 사용하기도 한다.

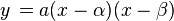$y\,=a(x-\alpha)(x-\beta)$ (단, $a \ne 0$ )

그래프 [편집]

$f(x) = x^2 - x - 2\,\!$

이차 함수 $y = a x 2 + b x + c$ 의 그래프는 포물선 형태이다.

최고차항 [편집]

이차 함수의 개형은 최고차항 a의 부호에 따라 다음과 같이 나눠진다.

a>0 일 때 아래로 볼록 (위로 오목)
a<0 일 때 위로 볼록 (아래로 오목)

판별식 [편집]

이차 방정식#근의 공식 문서를 참고하십시오.

이차 방정식 $a x 2 + b x + c = 0$ 의 해는 이차 함수 $y = a x 2 + b x + c$ 의 x절편이다. 따라서, 판별식 $D\,=b^2-4ac$ 의 값에 따라 x절편의 개수를 구할 수 있다.

D>0 일 때, 이차함수는 x축과 두 점에서 만난다.
D=0 일 때, 이차함수는 x축과 한 점에서 만나고, 접한다고 표현한다.
D<0 일 때, 이차함수는 x축과 만나지 않는다.

y절편 [편집]

이차 함수 $y = a x 2 + b x + c$ 에서 x에 0을 대입하면 y=c가 된다. 따라서 이차 함수의 y절편의 좌표는 (0,c) 이다.

축 [편집]

이차함수 $y = a (x - p) 2 + q$ 에서 $x = p + h$ 와 $x = p - h$ 를 각각 대입하면 $y = a h 2 + q$ 로 값이 같다. 따라서, 이차함수는 직선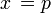 $x\,=p$ 에 대해 대칭이고, 이 직선을 축이라고 한다. 이차함수의 일반형에서 축의 방정식은 다음과 같다.

$x\,=-\frac{b}{2a}$

이차함수의 두 x절편을 알 때, 다음과 같이 구할 수 있다.

$x\,=\frac{\alpha+\beta}{2}$

꼭짓점 [편집]

이차함수와 축의 방정식의 교점을 꼭지점이라 하고 이차함수는 최고차항a의 부호에 따라 꼭지점에서 최대값 혹은 최소값을 갖는다.

아래로 볼록(a>0)일 때, 이차함수는 꼭짓점에서 최소값을 갖는다.
위로 볼록(a<0)일 때, 이차함수는 꼭짓점에서 최대값을 갖는다.

이차함수가 표준형과 일반형으로 주어졌을 경우 각각의 꼭짓점의 좌표는 다음과 같다.

표준형으로 주어졌을 경우

$(p\,,q)$

일반형으로 주어졌을 경우

$(-\frac{b}{2a},-\frac{b^2-4ac}{4a})$

그래프의 꼭짓점과 X절편으로 이루어진 삼각형 [편집]

이차함수 $y = a (x - p) 2 + q$ 에서 꼭짓점을 A, x절편들을 각각 B, C라고 할 때, △ABC의 넓이 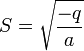$S=\sqrt {-q\over a}$ × $q$ 가 성립한다.

저작자표시 비영리 동일조건

'수학 (Mathematics) > 고,중학 수학 및 개념' 카테고리의 다른 글

극한값 , 발산 (0)	2012.11.02
자연대수 e 그래프 그리기 [영상강의] (0)	2012.11.02
포물선의 방정식 (0)	2012.11.02
일차함수, 일차 방정식,직선의 방정식 (0)	2012.11.02
양함수와 음함수의 미분 (0)	2012.11.02

3DMP