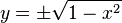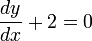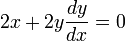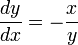출처 : 위키백과
양함수와 음함수의 예 [편집]
몇 가지 예를 통해 음함수와 양함수를 쉽게 이해할 수 있다.
일차함수 [편집]
다음 함수는 음함수이다.
- 2x − y − 1 = 0
이 식을 y에 대해 정리하면 양함수가 된다. 즉,
- y = 2x − 1
기본적으로 음함수로 표현된 모든 일차함수는 양함수로 표현가능하다.
원의 방정식 [편집]
다음 식은 원점을 중심으로 하는 반지름이 1인 원을 표현한다.
- x2 + y2 = 1
이것은 음함수이다. 그러나 하나의 독립변수에 대해 두 개의 종속변수가 할당되므로 이 식은 함수가 아니다. 본질적으로 이 식은 다음 두 개의 양함수를 합친 것이다.
이런 의미에서 일종의 함수로서 취급할 수 있고, 따라서 그 미분도 구할 수 있다.
역함수 [편집]
주어진 양함수의 역함수를 구하기 위해 독립변수와 종속변수를 바꾸면 즉시 음함수가 된다. 즉,
- y = f(x)
이 함수는 양함수이지만, 그 역함수를 구하기 위해 독립변수와 종속변수를 바꾼 다음 식은 음함수가 된다.
- x = f(y)
이 식을 양함수로 바꿀 수 있다면 다음과 같이 표현될 것이다.
- y = f − 1(x)
음함수의 미분 [편집]
미적분학에서, 음함수의 미분(Implicit differentiation)이란, 연쇄법칙(Chain rule)을 이용한 미분법을 말한다. 음함수를 양함수로 바꾸지 않고 미분한 다음, dy / dx를 계산한다. 이 결과는 양함수로 바꾼 후에 통상적인 미분을 시행한 결과와 같지만 계산이 수월하다는 장점이 있다. 그러나 경우에 따라 양함수로 먼저 바꾸는 쪽이 더 쉬운 경우도 있다.
예 1 : 일차함수 [편집]
다음과 같은 음함수를 미분하려고 한다.
- y + 2x = − 4
이를 양함수로 바꾸어 미분하면 다음과 같다.
이번에는 주어진 음함수에 대해 그대로 양변을 미분해보자.
간단한 미적분학의 지식을 통해 다음과 같이 됨을 알 수 있다.
그리하여 양함수를 미분했을 때와 동일한 결과를 얻게 된다.
예 2 : 원의 방정식 [편집]
단위원의 방정식이 주어져 있다.
- x2 + y2 = 1
양변을 미분하여 다음을 얻는다.
y2을 미분할 때 연쇄법칙(Chain rule)을 이용하였다. 또는 합성함수의 미분이라고 생각해도 좋다. 그래서 정리하면 다음과 같은 결과를 얻는다.
'수학 (Mathematics) > 고,중학 수학 및 개념' 카테고리의 다른 글
| 포물선의 방정식 (0) | 2012.11.02 |
|---|---|
| 일차함수, 일차 방정식,직선의 방정식 (0) | 2012.11.02 |
| 삼각함수의 역함수, 역수 구별 (1) | 2012.11.02 |
| 합성함수 (0) | 2012.11.02 |
| 삼각함수 sin,cos,tan 미분 (0) | 2012.11.02 |