함수의 극한
| 미적분학 | |||
|---|---|---|---|
| |||
x에 대한 함수 f(x)에서, x가 어떤 값 a에 한없이 가까워지면 f(x)도 어떤 값 c에 한없이 가까워질 때 f(x)가 c에 수렴한다고 한다. 이것을 기호로 표현하면,
 가 된다. 예를 들어, f(x)가
가 된다. 예를 들어, f(x)가 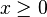 일 때 1, x < 0일 때 0을 가지는 함수라면
일 때 1, x < 0일 때 0을 가지는 함수라면 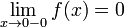 ,
,  이 된다.
이 된다.
0+0, 0-0의 경우 간단히 +0, -0으로 줄여서 표기하기도 한다. 또는 +0, -0을 줄여 +, -로 표기하기도 한다.
목차[숨기기] |
발산 [편집]
극한이 존재하지 않는 경우를 발산한다고 한다. 이때 함수값이 무한히 커지거나 작아지는 경우에는 특별히 양의 무한대로 발산하거나 음의 무한대로 발산한다고 정의한다.
예를 들어, 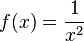 의 경우 x가 0에 가까워질 때 f(x)는 무한히 커지고, 따라서 양의 무한대로 발산한다.
의 경우 x가 0에 가까워질 때 f(x)는 무한히 커지고, 따라서 양의 무한대로 발산한다.
수학적 정의 [편집]
함수의 극한은 일반적으로 엡실론-델타(ε-δ)에 관한 방법으로 정의한다.
모든 양의 실수 ε에 대해, 어떠한 실수 δ가 존재하여 0 < | x − p | < δ일 때 항상 | f(x) − c | < ε가 성립하면, 이때의 극한값은
로 정의한다.
좌극한과 우극한도 비슷한 방법으로 정의하는데, 이때는 δ에 대한 조건이 0 < | x − p | < δ대신, 좌극한의 경우 0 < p − x < δ, 우극한의 경우 0 < x − p < δ가 된다.
===
x가 어떠한 값으로 접근하는 것이 아니라 무한히 커지거나 작아지는 경우에 대해서도 극한값을 정의할 수 있다. 이때의 조건은 모든 양의 실수 ε에 대해, 어떠한 실수 S가 존재하여 x > S(양의 무한대) 또는 x < S(음의 무한대)일 때 항상 | f(x) − c | < ε가 성립하는 경우이다. 이때 수식으로는 다음과 같이 표시한다.
- 양의 무한대:

- 음의 무한대:
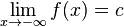
성질 [편집]
함수의 극한은 다음과 같은 성질을 지닌다.
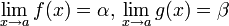 일 때 :
일 때 :

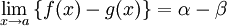
 (k는 상수)
(k는 상수)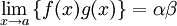
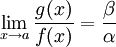 (단,
(단,  )
)
'수학 (Mathematics) > 고,중학 수학 및 개념' 카테고리의 다른 글
| 분수함수 미분 - 곱의 미분법으로 (0) | 2012.11.02 |
|---|---|
| 로피탈의 정리 (0) | 2012.11.02 |
| 자연대수 e 그래프 그리기 [영상강의] (0) | 2012.11.02 |
| 이차함수, 그래프 (0) | 2012.11.02 |
| 포물선의 방정식 (0) | 2012.11.02 |



 가 양의 무한대로 커질 때
가 양의 무한대로 커질 때  는
는 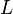 에 가까워진다.
에 가까워진다.