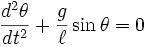선형성(線型性, linearity) 또는 선형(線型, linear, 라틴어: linearis)은, 직선처럼 똑바른 도형, 또는 그와 비슷한 성질을 갖는 대상이라는 뜻으로, 이러한 성질을 갖고 있는 변환 등에 대하여 쓰는 용어이다. 함수의 경우, 어떠한 함수가 진행하는 모양이 '직선'이라는 의미로 사용된다. 이러한 개념은 수학, 물리학 등에서 많이 사용된다. 다른 말로 1차(一次)라고도 한다. (단어 '1차' 자체는, '선형'을 의미하지 않는 경우도 많다.)
[편집]선형 사상
수학에서 선형성에 대한 정의는 다음과 같다.
함수  에 대해,
에 대해,
- 임의의 수
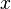 ,
,  에 대해
에 대해 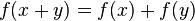 가 항상 성립하고
가 항상 성립하고 - 임의의 수
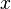 와
와  에 대해
에 대해  가 항상 성립할 때
가 항상 성립할 때
함수  는 선형이라고 한다.
는 선형이라고 한다.
(여기서 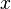 는 실수나 복소수, 또는 벡터 등 일반적으로 환상의 아벨 군의 원소이다. (α는 스칼라 곱을 의미))
는 실수나 복소수, 또는 벡터 등 일반적으로 환상의 아벨 군의 원소이다. (α는 스칼라 곱을 의미))
예를 들면, 일차함수의 경우, 원점을 지날 경우에 선형성을 갖는다.
선형대수학은 이러한 선형의 변환과 이로써 확보되는 공간의 성질에 대하여 연구를 하는 학문이다. 벡터 및 벡터 공간, 행렬을 이용하여 표시되는 선형사상 또는 선형방정식 계열에서 취급된다.
또한 함수를 함수로 투영하는 사상인 작용소(operator)의 선형성은 함수해석학에서 취급되고 있다. 함수의 미분을 작용소로 생각하여 얻어낼 수 있는 미분작용소(예: ∇ 나 라플라스 방정식)의 개념은, 선형 작용소의 중요한 예가 된다.
[편집]미분방정식에서의 선형성
미분방정식이 선형일 경우에는, 선형대수학의 수준으로 해를 찾아내는 것이 가능하다. 그러나, 카오스와 같이 선형이 아닌 (비선형인) 경우에는, 해를 구하는 것이 매우 어렵게 되어 버린다. 그러나 한편 팽르베 방정식과 같이, 어느 종의 대칭성을 가지고 있으며, 기하학적으로 다양한 성질을 내포하는 경우가 존재하는 등의 이유로, 수학자나 물리학자들의 관심의 대상이 되고 있는 것들 또한 비선형 미분방정식이기도 하다.
계, 변환 등이 비선형이라는 것은 그 구성요소의 합이나 곱 등 선형 결합으로 설명할 수 없다는 것을 뜻한다.
[편집]비선형 방정식의 예
비선형 방정식 중에는 다음과 같은 친숙한 것들도 있다.
또, 많은 다항식은 비선형 방정식이다. 그러나 연립 비선형 방정식은 훨씬 복잡하다. 게다가 다음과 같은 1차 상미분방정식
은 그 해를 구하는 방법이 널리 알려져 있다. (변수 분리) 그러나
 , 여기서
, 여기서 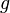 은 비선형 함수
은 비선형 함수
와 같은 고차 비선형 방정식을 푸는 것은 일반적으로 매우 어렵다. 비선형 편미분 방정식의 해는 더욱 구하기가 어렵다. 물론 해의 존재, 해의 안정성, 동역학에 대한 정리가 증명되어 있기도 하다.
단진자의 움직임을 기술하는 다음 비선형 미분 방정식을 보자.
일반적으로 이 방정식은  가 매우 작다는 가정을 하여
가 매우 작다는 가정을 하여  로 놓아 아래 선형 방정식으로 바꾸어 해를 구한다.
로 놓아 아래 선형 방정식으로 바꾸어 해를 구한다.
그러나  가 큰 범위를 진동한다면 진자의 비선형성은 진자의 움직임에 훨씬 크게 기여한다. 이 비선형 방정식에 의한 진자의 움직임은위상 평면, 타원적분 등의 방법을 이용하여 분석한다.
가 큰 범위를 진동한다면 진자의 비선형성은 진자의 움직임에 훨씬 크게 기여한다. 이 비선형 방정식에 의한 진자의 움직임은위상 평면, 타원적분 등의 방법을 이용하여 분석한다.
'수학 (Mathematics) > 고,중학 수학 및 개념' 카테고리의 다른 글
| 코사인 제 2법칙 (제 1, 2 코사인 법칙) 증명 (1) | 2012.11.02 |
|---|---|
| 삼각형 공식 정리 ,직각삼각형 닮음 공식,파푸스의 중선 정리,내,외각의 이등분선 공식 (0) | 2012.11.02 |
| 테일러 급수 전개 [제대로 정리편] (0) | 2012.11.02 |
| 복소수 (0) | 2012.11.02 |
| 특수치환 (삼각치환, 지수식치환, 루트치환), 삼각함수 쉬게 외우기 (0) | 2012.11.02 |