픽킹

픽킹이란 2D 스크린 좌표를 3D 좌표로 변경한 후 동일한 공간 내에서 교차 판정 하는 것이다.

 

여기서 중요한 것은 2D 좌표를 3D 좌표로 변경한다는 것이고, 동일한 공간! 내에서 교차판정한다는 것이다.

동일한 공간이 중요하다.

지형의 좌표가 존재하는 공간이 월드 공간이기 때문에 반드시 월드 공간으로 바꿔줘야한다.

 

과정을 간단히 말하자면,

1. 윈도우 좌표를 3D 좌표로 변경시킨다.

2. 폴리곤과 충돌체크를 한다. (IntersectTriangle)

이다.

 

픽킹이 처음에 어렵게 느껴지는 이유는 이 IntersectTriangle 함수가 프로그램을 위해 최적화된 함수로 몇몇 과정들이 축소되어있기 때문이다.

 

 

( Picking에 관한 코드는 Dx SampleBrowser에도 존재 하니 그걸 참고하세용 ~ 저도 그걸 참고해서 했어용>,<! )

 

 

먼저 2D 좌표에서 3D 공간 Ray를 뽑아내는 것을 보겠다.

 

 

<설명>

 

1) 윈도우 좌표를 알아낸 후

 

2) 공식을 통해 3D 좌표로 변경시킨다.

 

3) m_vOrig 는 카메라의 위치이고, m_vDir은 Ray의 방향이다. 

m_vDir에 3D 벡터 Ray를 설정한다.

 

4) 카메라 공간 좌표를 월드 공간 좌표로 변경하기 위해 뷰행렬의 역행렬을 곱한다.

여기서 주의해야 할 점은 m_vOrig는 D3DXVec3TransformCoord이고, m_vDir은 D3DXVec3TransformNormal라는 점이다.

왜냐하면 Coord는 위치를 변환하는 것이고, Normal은 벡터를 변환하는 것이다.

 

5) m_vDir 을 정규화하면 Ray가 완성된다.

 

 

이제 폴리곤과 충돌체크를 하는 IntersectTriangle 함수를 알아보겠다.

앞서 말했듯 이 함수는 몇몇 식이 축약됬기 때문에 이해하기가 어렵다.

 

BOOL IntersectTriangle

(D3DXVECTOR3& v0,D3DXVECTOR3& v1,D3DXVECTOR3& v2, FLOAT* t,FLOAT* u,FLOAT* v);

 

m_vOrig는 월드 공간 상의 카메라의 원점이고, m_vDir은 Ray의 방향이다.

v0, v1, v2 는 삼각형 정점의 위치이다. 

t는 vOrig에서 v0까지의 거리이다.

u는 v0에서 v1의 비율이고, v는 v0에서 v2의 비율이다

 

 

 

점 p(벡터 p)가 v0,v1,v2내에 있는지 판단하는 방법은 벡터로 한다. 

만약, 삼각형을 △OAB라고 할 때, 벡터 P가 삼각형 내에 있을 조건은

 

1) u ≥ 0

2) v ≥ 0

3) u + v ≤ 1 

 

이다. 때문에 u와 v를 구해 점 p가 폴리곤 내에 있는지 판단한다. 

 

 

 

 

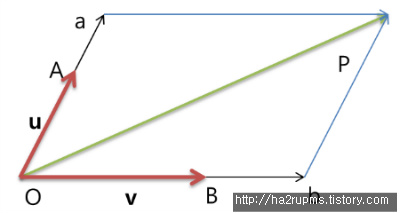
위 그림을 보면

 

v = ｜Ob｜/｜OB｜ 이다. (왜냐하면, ｜OB｜= ｜Ob｜ * v 니까.)

 

nA라는 A의 법선벡터를 구한다.

 

 

 

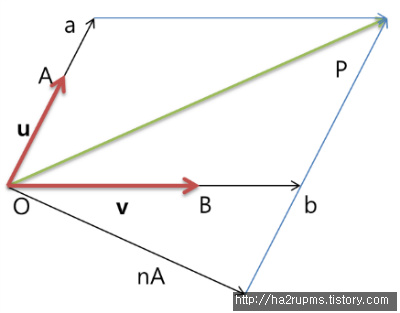
v = ｜Ob｜/｜OB｜

 

이 식의 분모와 분자에 nAcosΘ 를 곱한다.

 

v = ｜Ob｜ nAcosΘ /｜OB｜ nAcosΘ 

 

이것은 내적을 풀어쓴 것으로 

 

v = Ob · nA / OB · nA 

라고 할 수 있다.

 

그런데 nA에 투영했을 때, OP와 Ob의 정사영이 같으므로 

 

v = OP · nA / OB · nA

 

라고 할 수 있다. 이와 마찬가지로 

 

u = OP · nB / OA · nB

 

라고 할 수 있다.

 

 

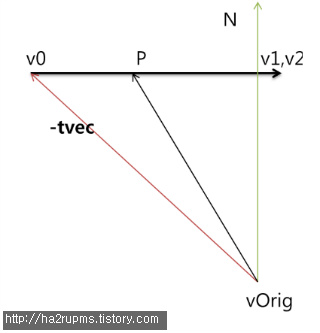
N을  v0와 v2의 평면의 법선벡터라고 하자.

여기서 (vOrig – v0) · N = (P – v0) · N 의 정사영이 같음을 볼 수 있다.

따라서 N = vDir × (v2 – v0) 이다. 

 

 

t는 거리라고 했다.

 

tvec = vOrig – v0

e1 = v1 – v0

e2 = v2 – v0

 

라고 하자.

 

u = OP · nB / OA · nB

 

에서 OP는 거리이므로 tvec으로 고칠 수 있다. 그리고 nB는 위에서 법선벡터 N을 구했으므로 vDir x e2 라고 할 수 있다.

 

따라서, 

 

u = tvec · (vDir x e2) / e1 · (vDir x e2) 

v = tvec · (vDir x e1) / e2 · (vDir x e1) 

 

이렇게 구한 u와 v를 통해 p가 삼각형 내에 있는지 판단하는 것이다.

 

IntersectTriangle은 이 식을 풀어서 쓴 것이다.

 

마지막으로 거리 t 를 구하기 위해서 분모를 fDet로 놓는다.

 

fDet = e1 · (vDir x e2) = vDir · (e1 x e2)

 

[ fDet 가 0이면, Ray가 같은 평면이고, 0보다 작으면 뒤에서 쏜 Ray, 0보다 크면 앞에서 쏜 Ray이다. ]

[평면의 방정식이 0보다 크면 Ray가 앞에 있는 것이다.]

 

 

 

위의 식에서

 

｜P - vOrig ｜ = t * ｜vDir ｜

 

이다. 따라서

 

t = ｜P - vOrig ｜/ ｜vDir ｜

 

분모, 분자에 ｜N｜cosΘ 를 곱하면

 

t = ｜P - vOrig ｜ ｜N｜cosΘ  / ｜vDir ｜ ｜N｜cosΘ 

 

이고, 이것은 내적을 풀어쓴 것이므로 정리하면

 

t = (P - vOrig) · N / vDir · N 

 

이다. 근데 (P - vOrig)과 –tvec의 법선벡터 N에 대한 정사영이 같으므로

 

t = -tvec · N / vDir · N 

 

이다.

 

 

 

ref : https://showmiso.tistory.com/140