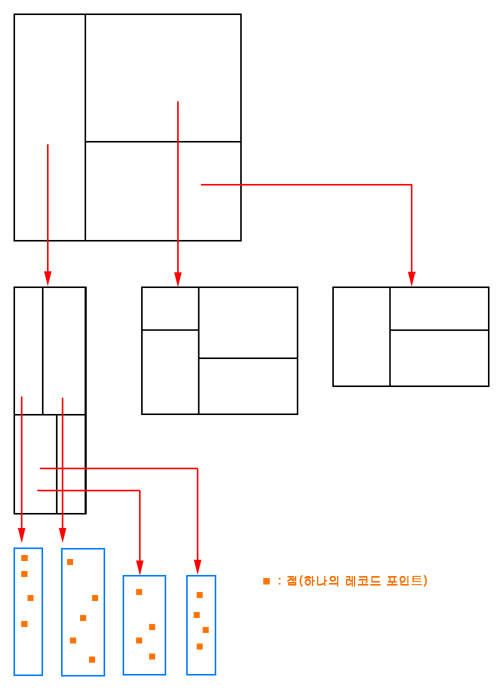
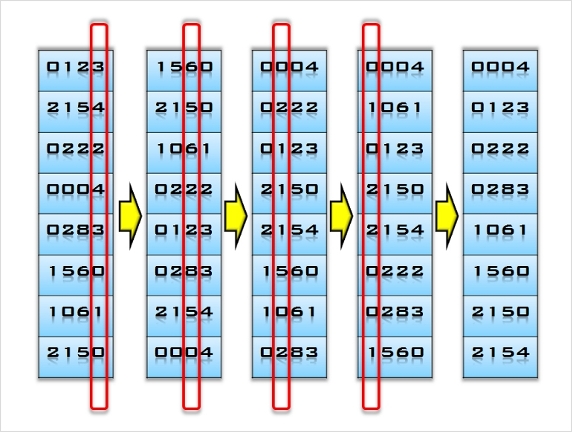
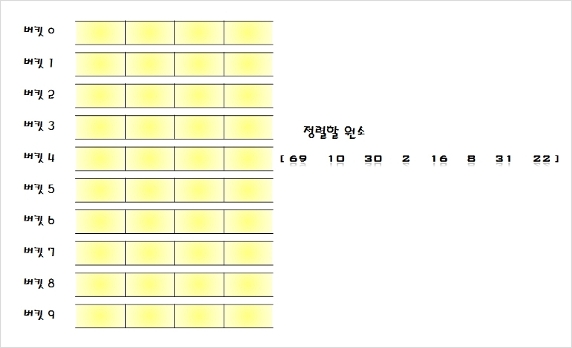
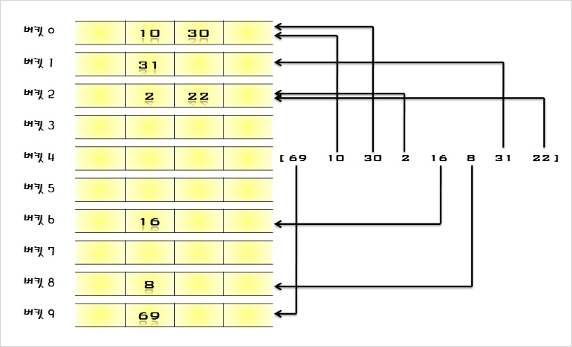
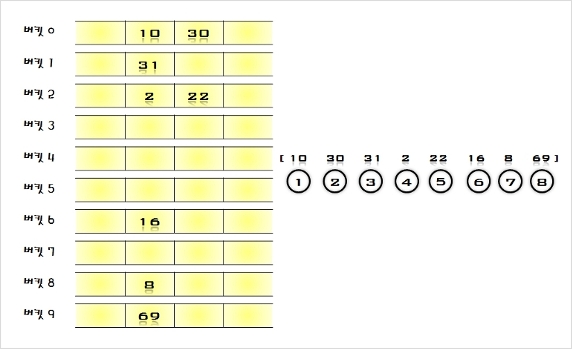
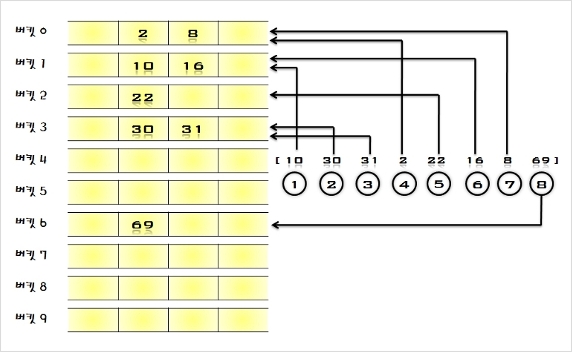
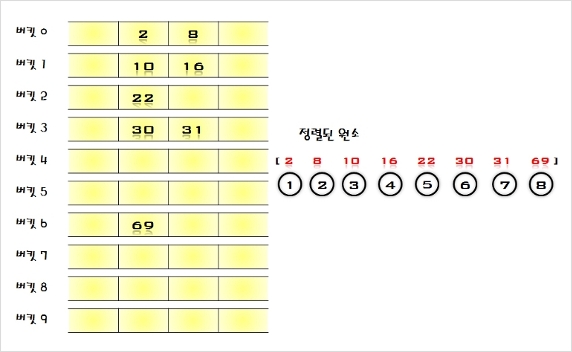
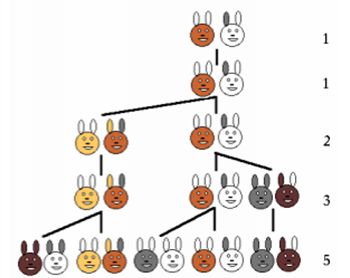
시스템들이 내부적으로 사용하는 검색 구조( 데이타베이스, 오라클 등등 => 인덱스 검색 구조이다)
외부검색에 적절한 형태 => 하드디스크 Tap 등 외부 장치의 검색에 잘 사용됨
내부검색 => 램 같은 내부적인 부분
이진트리 문제점 : 좌우 균형이 맞지 않으면 비효율적이다
트리의 성능은 트리의 높이에 있다
그래서 트리의 높이를 낮춰주면 성능이 올라갈 수 있다
그래서 트리의 좌우 균형을 맞춰 주는 것이 중요하다
균형트리 : 삽입 삭제시 필요하면 스스로 균형을 유지하는 트리
AVL, 2-3(-4), Red-Black Tree-BTree....
-삽입은 split (분할) 동작 으로 삽입
Balanced Tree : 스스로 균형을 유지하는 트리

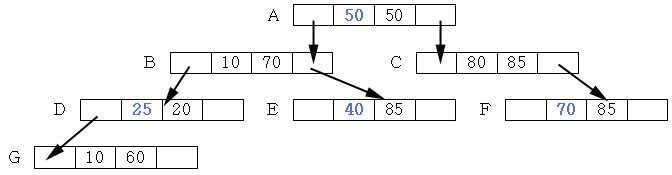
A 를 찾기 위해서 균형이 안맞으면 느릴 수 있다
균형이 안맞으면 링크드 리스트처럼 검색성능을 보인다
위 그림은 트리를 회전함으로써 이진트리의 규칙을 유지하면서 트리의 높이를 낮추는 방법을 보여준다
RB Tree & B Tree 의 방법에 AVL Tree 가 포함된다
하나의 노드에 여러개의 노드가 들어올 수 있다
M 차 => 한 노드에 자료가 가장 많이 들어간 수의 차수를 말한다

이 그림에서 M = 5차 > v,w,x,y,z
B - Tree 규칙.1
1. 노드의 자료수가 N 이라면 , 그 노드의 자식의 수는 N+1 이어야 한다 => left, right 가 있어야
하므로
자료수 = (노드 안에 있는 자료의 개수)
2. 각 노드의 자료는 정렬된 상태여야 한다 --> 방향으로
3. 노드의 자료 D_k 의 왼쪽 서브트리는 D_k 보다 작은 값들이고
D_k 의 오른쪽 서브트리는 D_k 보다 큰 값들이어야한다
( 이진트리에서 부모보다 왼쪽은 작은 트리, 오른쪽은 부모보다 큰 트리를 말한다 )
ex) 그림에서 C의 왼쪽은 C 보다 작은 A,B 이고, D,E 는 C 보다는 큰지만 F 보다는 작은 자료이다
B - Tree 규칙.2
1. Root 노도는 적어도 2개 이상의 자식을 가져야 한다.
2. Root 노드를 제외한 모든 노드는 적어도 floor(M/2) [<= 내림] 개의 자료를 가지고 있어야
한다.
( 위 그림에서는 노드들이 모두 적어도 2개 이상의 자료를 가지고 있다
3. 외부 노드(leaf node) 로 가는 경로의 길이는 모두 같다
4. 입력자료는 중복될 수 없다.( list 등을 같이 쓰면 중복을 허용 할 수도 있다 )
B-Tree 구조
시작을 나타내는 노드가 있는데 헤드에 대한 포인트 노드만 사용하고 끝은 0 로 처리 해서 만든다
끝을 NULL 로 처리 하는 것이 가능
[노드 안의 글자가 '키' 를 의미한다]
B-Tree 검색
루트에서부터 노드의 자료들과 찾을 값을 비교하여 노드가 찾을 것보다 작으면 왼쪽 크면 오른쪽으로 이동하면서 찾아간다
-노드내에서는 순차검색, 전체적으로는 트리검색
B-Tree 삽입
1.자료는 항상 leaf 노드에 추가된다 (leaf 노드의 선택은 삽입될 키의 하향 탐색에 의해
결정)
2. 추가될 leaf 노드에 여유가 있다면 그냥 삽입
3. 추가될 leaf 노드에 여유가 없다면 '분할' 하기
4. 삽입할 때 같은 키 값이 있으면 안됨으로 해당 노드에 삽입하기 전에 같은 값이 있는지 find 해봐야 한다

[루트노드 분할]
위 그림은 왼쪽은 Root(뿌리) 노드일경우에 가능한 경우이다
H 를 넣으려고 할때 노드를 3개로 분할 한 후 H 를 넣는 모습
Root 노드이기 때문에 floor(M/2) 와 관계 없이 G 가 하나로 존재 가능하다 G 가 루트가 되는 것
[일반노드 분할]
위 그림의 오른쪽이 일반노드에 대한 분할인데
만약 A B C D E 노드를 C 를 중심으로 분할 한다면 C 를 부모노드로 올려주고 C 를 기준으로
A B 를 왼쪽 D E 를 C 의 오른쪽 노드로 배치시켜서 분할 한다
(M 이 홀수 인 경우로 가정 =>
현재 차수 M = 5 로 가정 하였으므로 5/2=2 2개씩 나누어야 반씩 나눠 짐으로 왼쪽
두개,
오른쪽 두개 로 나눈다 3번째가 부모로 올라가는 형태 )
이때 부모로 올려야 하는 문제가 있는데 그것은 부모가 꽉찬 노드 일경우에 발생한다
이때는 부모를 분할 한 후 그다음 원래 분할 하려고 했던 노드를 분할 한다
분할 => split
* 삽입할때 현재 중간 노드들이 풀이면 M(차수) 만큼 풀이면 분할을 하고 그 위치에서 다시 삽입할 위치를 찾아간다 => 미리 분할
해 준다
- 마지막 leaf 노드까지 가서 마지막 leaf 노드가 풀이면 분할 후 삽입한다
[ 외부노드(leaf node) B-Tree 삭제]
삭제하고자 하는 자료가 있는 노드에 자료를 삭제 후 자료수가 M/2 이상이 되도록 보장해야 함
루트를 제외한 모든 노드는 M/2 보다 자료수가 많아야 한다, 이것이 보장 되어야 B-Tree 이다
이것의 해결 방법이 형제에게서 빌리기 VS 형제와 결합하기 이다
1. 빌리기 : 형제가 M/2 보다 맣은 자료를 가지고 있다면 빌려온다
2. 결합하기 : 형제에게서 빌릴 수 없다면=>M/2 보다 작다면 합친다

[형제에게서 빌리기] - Borrow key => 회전
왼쪽 그림은 B 를 삭제 하려고 하는데 A 하나 밖에 자료가 안남게 된다
그래서 D 를 빌려 올려고 하지만 D 를 A 노드 쪽으로 가져오면 부모인 C 와 순서(왼쪽이 작은쪽) 이 맞지 안으므로
D(형제) 를 부모 에게 주고 C 를 A 노드 쪽으로 주게 되면 => [자료를 돌리는 식]
B 를 삭제 할 수 있게 된다( 오타 : 그림상에서 D K 는 D G K 이다 )
이렇게 B Tree 의 규칙을 어기지 않고도 Balance 조정이 가능하다
[형제와 결합하기] - BindNode => 중간이 되는 부모 자료와 같이 결합하기
오른쪽 그림은 결합하기인데
B 를 삭제하기위해서 보면 A 가 있는 노드의 자료가 하나만 남기 때문에 그냥 지워선 안되고
D를 빌려오자니 D 와 함께 있는 E 가 하나만 남게 되어 빌려오는 상황도 여의치 안다
그래서 이때는 결합하기로 가야한다
먼저 A B 와 D E 중간에 위치한 부모의 C 를 아래로 내려서 그림과 같이 A B C D E 로 합친다 그 후 B 를
제거
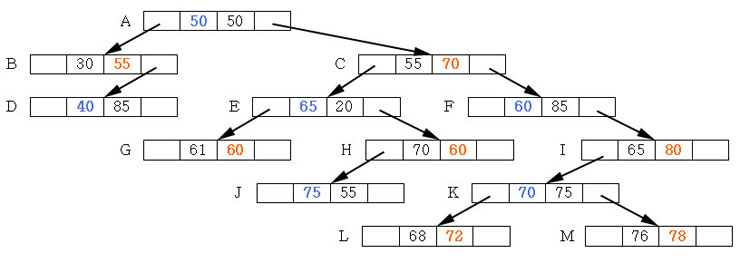
[ 내부노드(leaf node가 아닌 ) B-Tree 삭제]

1.
i 를 삭제 하려고 할때 I 를 제거 하면 i 를 삭제하고 재 구성할 수 없으므로 대채하는 것으로 가야한다 => 키 순서상 재구성이
힘들다
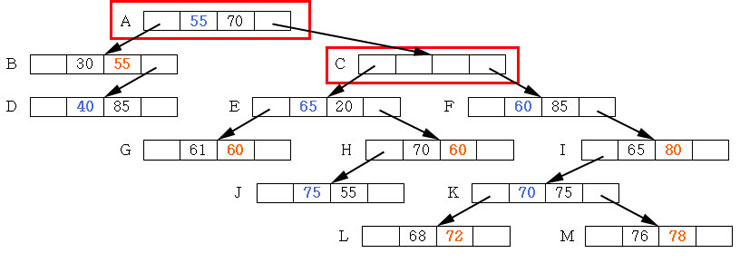
이진트리와 동일하게 i 보다 바로 작은값 또는 i 보다 바로 큰 값으로 대채한 후 대채한 값을 삭제 하면 된다
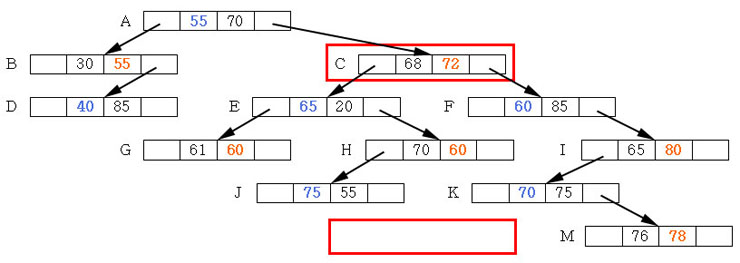
Right Subtree 중 가장 작은 값인 J 로 i 대신 대채한 후 j 를 다시 삭제 하러 가면 된다
이때 j 를 삭제하기 위해 내려갈때 삭제시 M/2 이하인 노드는 형제에게서 빌리든지, 결합을 해야 한다
=> 삭제를 할때 부족한 노드가 있으면 안됨으로 balance 를 유지하기 위해
2. bindNode 를 할때 오른쪽 노드를 왼쪽으로 결합 하면 오른쪽 노드는 없어지게 되고 부모노드에 있는 자료중 하나가
아래려 내려 오게
되는데 이때 부모가 root 이고 부모의 자료 개수가 0 개가 된다면 합쳐진 왼쪽 노드를 부모노드로 해주면
된다
3. swap 루트에서 오른쪽으로 한번 이둥후 왼쪽으로 계속이동하면 I 보다 바로 큰 값을 찾을 수 있다
그 후 대채할 키를 다시 루트에서부터 삭제하는과정을 거치면 된다

이진트리의 경우 레벨(높이) 는 (log_2 N)+1 이하 이다 이때 밑이 2 인 것은 이진트리에서 자식은 2개씩 나갈수 있기 때문
B-Tree 의 경우 자식은 최소 M/2 개 이상이어야 함으로 밑이 M/2 이다
삽입/삭제/검색 성능 complexity 를 말할때는 굳이 밑을 쓰진 않는다 O(logN) 으로 성능이
좋다
-이진트리의 경우 평균 시간 복잡도가 nlogn 이며 최악의 경우 n 의 시간 복잡도를 갖는다
이를 보안할 것이 AVL-Tree, Red-Black Tree , B-Tree , Splay Tree 등이 있다
-최악의 경우가 없다
-차수가 높을 경우 노드내에서 순차검색대신 이분검색을 사용 하는 것도 속도를 높일 수 있는 방법이다
-모든 leaf 가 같은 레벨에 위치한다
tip : AVL Tree = leaf node 의 차이를 2 이하로 구성하는 트리 삽입시 이를 위반하면 자동 재구성한다
splay tree = 가장 최근에 사용된(삽입 삭제 검색) 노드를 루트로 항상 유지하는 트리이다
스케줄 알고리즘 등에서 LRU(Least Recently Used => 페이지교체 알고리즘) 같은 알고리즘을
구현하는데 적합