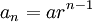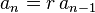무한급수 :: 3DMP

무한급수

2012. 11. 2. 20:44

등비수열(等比數列)은 각 항이 그 앞 항과. 일정한 비를 가지는 수열을 말한다. 그리고, 이 일정한 비를 공비(共比)라고 한다.

첫항이 a이고 공비가 r인 등비수열은 다음과 같다.

$a, ar, ar^2, ar^3, \cdots$

ex)

∞

∑ ( -1/3 )^n

n=1

은 위 조건식에 맞춰 n=1 일때가 첫항 a 가 된다 즉

a=(-1/3)^1 = -1/3

ar=(-1/3)^2 = 1/9

임으로 공비는

ar=(-1/3)^2 = 1/9

r=((-1/3)^2)/a = (1/9)/a

r=((-1/3)^2)/(-1/3) = (1/9)/(-1/3)

r=(1/9)/(-1/3) = (1/9)/(-1/3)

r=-3/9 = -3/9

r=-1/3 가 된다.

급수(級數)란 수학에서 수열들의 각 항의 합을 의미한다. 즉, 급수란 여러 수들의 합연산으로 표현된다. 급수의 예로는 아래와 같은 등차수열의 합이 있다.

1 + 2 + 3 + 4 + 5 + ... + 99 + 100

등비수열의 예 [편집]

첫항이 1이고 공비가 2인 등비수열은 다음과 같다.

1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, ...

첫항이 729이고 공비가 2/3인 등비수열은 다음과 같다.

729, 486, 324, 216, 144, 96, 64, ...

첫항이 3이고 공비가 -1인 등비수열은 다음과 같다.

3, -3, 3,-3, 3, -3, 3 ...

기본적 성질 [편집]

첫항이 a이며, 공비가 r인 등비수열의 n번째 항은 다음과 같다.

$a_n = a r^{n-1} \;$

등비수열은 n ≥ 1에 대해다음과 같은 점화식으로 표현될 수 있다.

$a_n = r \, a_{n-1}$

이를 이용해, 일반적으로 어떤 수열이 등비수열인지 확인하기 위해서는 각각의 연속된 항의 비가 일정한지만 확인하면 된다.

등비수열은 공비에 따라 여러 경향을 보이는데 만약 공비가

양수이면, 모든 항은 첫항과 같은 부호를 가진다.
음수이면, 계속 부호가 번갈아 가며 나타난다.
1보다 크면, 양의 무한대를 향해 지수적으로 증가한다.
1이면, 모든 항의 값이 같아진다.
-1과 1사이에 있지만 0이 아니면, 0을 향해 지수적으로 감소한다.
-1이면, 모든 항의 절대값은 같지만, 부호가 계속 번갈아 가며 나타난다.
-1보다 작으면, 음의 무한대를 향해 지수적으로 증가한다.

등비수열은(공비가 -1, 1, 0이 아닌경우) 등차수열과 같이 선형 변화를 보이는 것과 달리, 지수적 변화를 보인다. 이 두 수열은 관계가 전혀 없어 보이지만, 등차수열에 거듭제곱을 취하면 등비수열이 되고 반대로 등비수열의 각 항에 로그를 취하면 등차수열이 되는 관계를 가지고 있다.

등비중항 [편집]

0이 아닌 세 수 $a$ , $b$ , $c$ 가 이 순서로 등비수열을 이룰 때, $b$ 를 $a$ 와 $c$ 의 등비중항이라 한다.

따라서 세 수 $a$ , $b$ , $c$ 에 대하여, $b$ 가 $a$ 와 $c$ 의 등비중항이라면

$\frac{b}{a} = \frac{c}{b}$ 즉,

b 2 = a c

가 성립한다.

또 $b 2 = a c$ 에서 $b=\pm\sqrt{ac}$ 이므로 등비중항은 양수와 음수로 2개이다.

등비수열의 합 [편집]

$a 1$ 부터 $a n$ 까지 더한 합인 등비급수 $S n$ 은 다음과 같이 구할 수 있다.

$S_n = a+ar^1+ar^2+ar^3+ \cdots +ar^{n-1}$

$= a(1 + r^1 + r^2 + \cdots + r^{n-1})$

여기에서 $r$ 의 값이 1이 아니라면, 다음과 같이 정리할 수 있다.

$S_n = a\frac{(1 + r^1 + r^2 + \cdots + r^{n-1})(r-1)}{r-1}$

$= a\frac{r^n-1}{r-1} = a\frac{1-r^n}{1-r}$

무한등비급수 [편집]

무한등비급수는 등비수열의 각 항을 무한히 더한 합으로 다음과 같이 정리된다

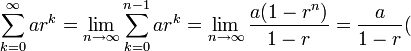$\sum_{k=0}^\infty ar^k = \lim_{n\to\infty}{\sum_{k=0}^{n-1} ar^k} = \lim_{n\to\infty}\frac{a(1-r^n)}{1-r} = \frac{a}{1-r} ($ 단 |r| < 1 일 때)

lim n->∞ a(1-r^n)/(1-r)

= lim n->∞ a/(1-r) - ar^n/(1-r)

임으로 |r| < 1 이면 ar^n 은 0 으로 수렴하고 - ar^n/(1-r) 또한 0 으로 수렴하게 되어 남는 ㅓㅅ은

lim n->∞ a/(1-r) 이 된다, 즉 이 값으로 수렴하게 된다 (|r| < 1 일때)

저작자표시 비영리 동일조건

'수학 (Mathematics) > 고,중학 수학 및 개념' 카테고리의 다른 글

3,4 차 함수 그래프 [영상강의 링크] (0)	2012.11.02
닮은비, 넓이의 비 (0)	2012.11.02
거듭제곱근 강의 [영상강의링크] (0)	2012.11.02
기초수학관련 문제 및 풀이 (0)	2012.11.02
절대값과 그래프 중 \|Y\| = f(x) 의 경우... (0)	2012.11.02

3DMP