Dijkstra
다음과 같은 노드가 있다 가정하에 접근해봅니다



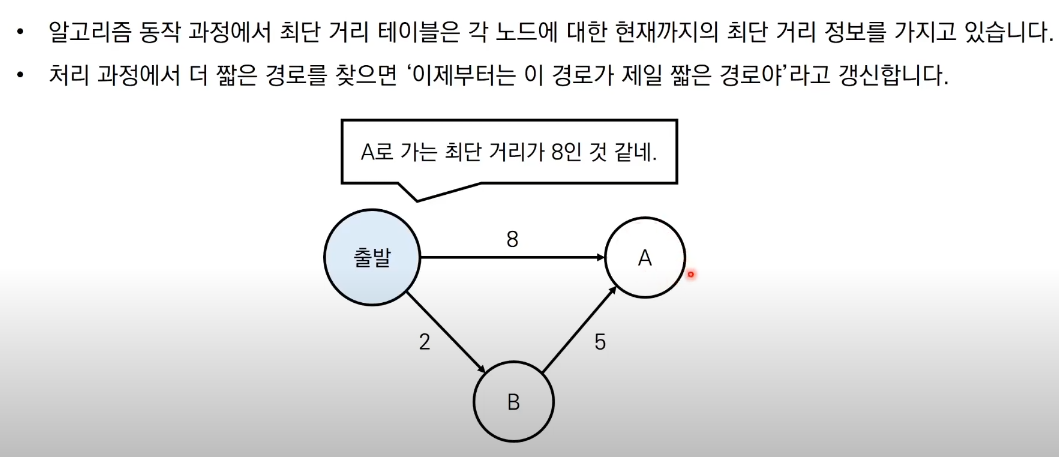
출발에서 A 로 갈때 미리 8을 a 까지드는 비용을 누적으로 구해놓고
출발 -> B -> A 로 가는 경로가 누적적으로 구해지면서 A에 도달했을때 기존 누적값과 누적해서 공통인 노드에 도달했을때 즉 A 에 도달했을때 누적된 것 중 더 빠른 거리를 경로로 선택하는 것
using System;
namespace GraphTraversal
{
class Graph
{
// -1 은 연결 안된 상태를 표시
int[,] adj = new int[6, 6]
{
{ -1, 15, -1, 35, -1, -1 },
{ 15, -1, 5, 10, -1, -1 },
{ -1, 5, -1, -1, -1, -1 },
{ 35, 10, -1, -1, 5, -1 },
{ -1, -1, -1, 5, -1, 5 },
{ -1, -1, -1, -1, 5, -1 },
};
public void Dijikstra(int start)
{
bool[] visited = new bool[6];
int[] distance = new int[6];
Array.Fill(distance, Int32.MaxValue);
int[] parent = new int[6];
distance[start] = 0; //자기자신은 0 거리로 만든다
parent[start] = start; //자기자신의 부모는 자기자신으로
while (true)
{
// 제일 좋은 후보를 찾는다.
// 가장 유력한 정점의 거리와 번호를 저장한다.
int closet = Int32.MaxValue;
int now = -1;
for (int i = 0; i < 6; i++)
{
// 이미 방문한 정점은 스킵
if (visited[i])
continue;
// 아직 발견(예약)된 적이 없거나, 아직 방문하지 않고 거리만 계산한 노드 중에서 가장 짧은 노드를 찾아내기 위한 과정
if (distance[i] == Int32.MaxValue || distance[i] >= closet)
continue;
closet = distance[i];
now = i;
}
//now : 아직 방문하지 않은 노드 중 가장 짧은 거리가 짧은 노드
if (now == -1)
break;
visited[now] = true;
for (int next = 0; next < 6; next++)
{
// 연결되지 않은 정점은 스킵한다
if (adj[now, next] == -1)
continue;
// 이미 방문한 정점은 스킵
if (visited[next])
continue;
//now : 1 ,
//next : 3
// 새로 조사된 정점의 최단 거리를 계산한다.
// 15 + 10
int nextDist = distance[now] + adj[now, next];
// 이전까지 누적해서 계산 했던 노드 길이distance[next]보다,
// 현재 계산하고있는 누적 길이(nextDist)가 더 작다면 next Dist 즉 더 짧은 경로로 변경한다
if (nextDist < distance[next])
{
distance[next] = nextDist; //해당 노드의 현재 까지 짧은 거리
parent[next] = now; //해당 노드의 현재까지 짧은 거리의 부모
//각 노드에 누적된 거리가 계속 갱신 됨으로
}
}
}
}
}
class Program
{
static void Main(string[] args)
{
Graph dijik = new Graph();
dijik.Dijikstra(0);
}
}
}
실행 결과

벨만 포드 알고리즘과 다익스트라 알고리즘의 가장 큰 차이점은 벨만 포드 알고리즘은 방향 그래프에서 음의 가중치를 지닌 간선이 존재해도 사용할 수 있다 라는 점입니다. 따라서 음의 가중치를 가진 방향 그래프를 주면서 최단 거리를 구하라고 한다면 다익스트라 알고리즘이 아닌 벨만 포드 알고리즘을 사용 해야 합니다.
ref : 한곳 더 있는데 url 을 잊어버림
https://www.youtube.com/watch?v=F-tkqjUiik0
반응형
'프로그래밍(Programming) > C#' 카테고리의 다른 글
| A* (Astar) , JPS (0) | 2022.10.28 |
|---|---|
| Tree height (0) | 2022.10.27 |
| BFS 길찾기 (0) | 2022.10.26 |
| Comparer<T> Class (0) | 2018.10.15 |
| out var (0) | 2018.09.09 |

