rand() 함수에 대해서...

http://blog.niu.kr/21

rand() 함수에 대해서...

전에 면접을 보고 rand() 함수에 대해 조금 자세하게 자료를 모아 봤습니다.

일반적으로 rand()함수는 random한 값을 가지게 됩니다.

하지만 그냥 rand()함수를 쓰게 되면 항상 같은 결과가 나오는걸 볼수 있는데 이건 왜 이럴까요?

이건 rand 함수가 항상 새롭게 랜덤한 수를 생성하는게 아니고 일정한 난수표를 가지고 있기 때문에 이러한 결과가 나오게 됩니다. 그래서 유사난수 생성기(pseudorandom number generator)라고 부릅니다. 그리고 이 난수표를 결정하는것이 바로 종자값이라고 부르는 seed 입니다.
그리고 이 시드값을 결정해 주는 함수가 바로 srand()인것입니다.

하지만,

 srand(1);
 printf("%i %i %i\n", rand(), rand(), rand());

같은 프로그램을 돌려보면 실행할때마다 세개의 값이 항상 같은것을 알수 있습니다.
그래서 이 시드값을 정할때는 시간을 초단위로 돌려주는 time 함수를 사용하게 됩니다.

 srand(time(NULL));
 printf("%i %i %i\n", rand(), rand(), rand());

보통 0~9까지의 랜덤한 숫자를 얻을때 rand()%10 처럼 나머지 연산자를 사용하게 되는 경우가 많은데 이경우 큰 결점이 생기게 되는데 이는 나머지 연산자가 상위비트들을 잘라내므로 기존 rand 함수가 생성하는 수의 패턴인 20억보다 훨씬 짧은 주기의 수치들이 나오게 됩니다. 반복되는 패턴이 더 적은 효과적인 난수 생성기를 만들기 위해서는 발생된 수의 하위비트들이 아닌 상위비트들을 사용해야 하는데 이를 위해서는 나누기를 이용합니다.

 rand() % 10; 
 rand() / (RAND_MAX/10.0f);

둘다 같은 0~9까지의 숫자를 가져오지만 실제로는 그렇지 않다. rand 함수는 0~RAND_MAX의 값을 가져오게 되는데 VC6에서 RAND_MAX의 값은 0x7FFF이기 때문에 골고루 분포된 값을 가지기 힘들다. 이를 테스트해보기 위해서 0~999의 숫자를 생성하는 함수를 10000000번 호출하는 프로그램을 만들어 해당 분포도를 체크하였다.

결과에서 알수 있는것은 0x7FFF 즉 0~32767의 숫자를 생성하기때문에 이를 1000으로 나머지 연산을 하게 되면 나머지가 0~767인 숫자는 33번, 768~999인 숫자는 32번이 된다. 그렇다면 평균적으로 나머지가 0~767인 숫자는 10000000/32768*33=10070번, 768~999인 것은 10000000/32768*32=9765번이 나오게 되며 위와같은 그래프가 나오게 되는 것이다. 즉, 비교적 안정된 난수를 얻고 싶으면 나누기 연산을 사용하자( ..)a

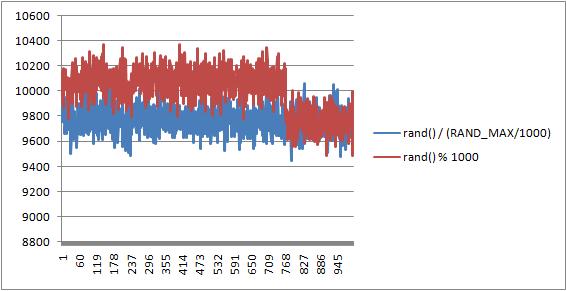
추가적으로 rand() 보다 표준편차가 더 적은 난수 알고리즘이 있으니 바로 Mersenne Twister, MT19937라고도 하고 MT알고리즘이라고도 부르는 메르센 트위스터입니다. 소스는 http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/emt.html 에서 받을수 있고, init_genrand(seed)로 시드를 결정(=srand), genrand_int32()로(=rand) 32비트의 정수를 생성할수 있습니다.

하지만 이 난수를 발생하는 알고리즘들은 표준편차가 적은 일직선의 그래프가 나옵니다. 그렇다면 난수가 정규분포를 가지게 하려면 어떻게 해야 할까요?

이전 면접때 이 질문에서 턱 막히더군요-_-) 대답은 간단합니다.
난수를 더하면 됩니다;;
가령 0~1000의 정규분포를 가지는 가지게 하고 싶다라면 0~100까지의 난수를 10번 생성해서 더하면 됩니다.
아마 검색해보면 일반적으로 -1~1까지의 정규분포를 가지게 만드는 것을 찾을수 있을겁니다.

소스보기

less..

for( inti=0 ; i<1000 ; i++ )
{
    cout << val = randND( 70.0f ) << endl;
}


floatrandND( floatcenter )
{
/*
X_i = (0,1)

     sum(X_i) - n/2
Z = ----------------
       sqrt(n/12)

if n=12,
then Z=sum(X_i) - 6

*/
   floatsum=0.0f;
    for( inti=0 ; i<12 ; i++ ) // 12회 루프도는 것은 전통적인 이유때문이다.
   {
        sum += rand_0_1();
    }
    sum -=6.0f;
    returnsum+center;
}

floatrand_0_1()
{
    return(float)rand()/RAND_MAX;
}
출처 : http://www.gpgstudy.com/forum/viewtopic.php?t=4339&highlight=%C1%A4%B1%D4%BA%D0%C6%F7

less..

난수를 많이 더하면 더할수록 그래프는 정규분포에 가깝게 나오지만 일반적으로는 12번을 사용하는군요-_-
경험적인 수치라고 합니다. 그냥 넘어갑시다=ㅁ=ㅋㅋ
그래서 적당히 6번을 더해보았습니다.

역시나 더하면 더할수록 종모양이 잘빠집니다-_-a
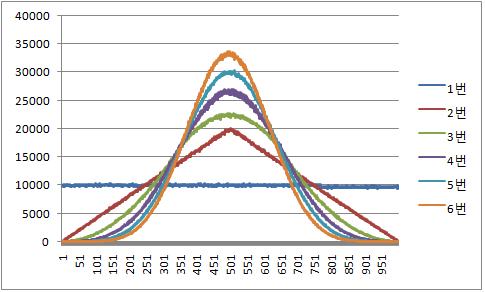
하지만 위의 소스가 아닌 단순히 0~1000/n 까지의 난수를 더한것이라 그런지 몇번 넘어가니 양쪽 끝이 거의 0에 가깝군요. 실제로는 7번정도의 데이터를 더해서 한다고 합니다.

이외에도 가우시안 함수를 이용한 정규분포 난수 생성기도 있습니다만...수학적으로 된것이라- _-)
설명이 불가능한 관계로 패스합니다.