http://fracton.khu.ac.kr/~comp/monte/monte.html
기본 수치 해석
Monte Carlo Integral
목적: 1.Gaussian Quadrature 등으로부터 계산할 수 없는 적분 값의 추정
2. 다중 적분(2 차원 이상의 적분)에 대한 처리 용이
3. 흉내내기(전산 시늉:simulation)의 기본인 난수(random number)에 대한 이해
1. Random Number(무작위수, 난수)란?
주어진 구간에서 어떤 특정한 순서 없이 특정한 주기 없이 임의의 부분 구간에 들어갈 확률이 일정한 수들의 열.
Random Number를 만드는 기본 Algorithm들
i) computer 내부의 cmos clock을 읽는 방법: CMOS clock time을 일정한 간격으로 읽어서 초단위로 환산한다. 이 시간의 열을
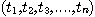 이라하고, (0,1000) 사이의 난수열을 얻고 싶으면,
이라하고, (0,1000) 사이의 난수열을 얻고 싶으면, 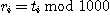 을 이용해 난수열
을 이용해 난수열 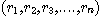 을 얻음.
을 얻음.
ii)middle-square method(von Neumann이 처음으로 제안)
(0,1000) 사이의 난수열을 얻을려면, 처음에 0과 1000사이의 임의의 수를 seed로 한 다음 그 seed를 제곱하여 얻은 수의 가운데 3 자리 수를
난수열의 처음 수로 하고 이수를 다시 제곱하여 얻은 수의 가운데 3 자리 수를 다음 수로 하는 방법등을 계속하여 난수열을 얻음.
예) 267(seed) -> 267^2=71829 -> 182(난수열의 첫 번째 수) -> 182^2 =33124 ->312(난수열의 두 번째 수) ->.....
ii) n번째 난수를 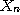 , n+1번째 난수를
, n+1번째 난수를 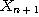 이라 했을 때 (0, m)사이의 난수열을 식
이라 했을 때 (0, m)사이의 난수열을 식
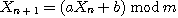
을 이용해 얻는 방법.
최종적으로는 i), ii), iii) 등의 방법으로 얻은 (0, m)사이의 난수열 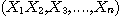 을 이용해 본인이 원하는 구간 (a, b) 사이의 난수열은 수식
을 이용해 본인이 원하는 구간 (a, b) 사이의 난수열은 수식
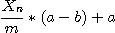
을 이용해 구할 수 있다.
Pseudo Random Number와 seed
아무리 좋은 algorithm을 사용해 난수열을 만들더라도, 언제 주기가 생기거나 또는 난수 자체가 반복하여 나타나거나, 특정한 부분 구간에 난수가 많이 모인다든지 하는 현상이 발생할 지 모른다. 이러한 의미에서 우리가 만든 난수열을 의사 난수(pseudo random number)열이라 부른다. 또 같은 난수 발생 algorithm을 반복해서 사용할 때, 나타나는 난수열은 seed(즉 난수열을 만들 때 도입하는 처음의 수)가 같으면 항상 같은 난수열이 만들어 진다. 따라서 어떤 난수열을 이용해 전산 시늉을 할 때, 이 전산 시늉을 반복해서 평균하여 결과를 얻는다면, 반복할 때 마다, 항상 다른 seed에서 출발헌 난수열을 사용하는 것이 좋다. 이러한 의미에서 seed를 흔히 전산시늉을 시작하는 시각을 초단위로 환산하여 사용하곤 한다.
Visual Basic에서 Pseudo Random Number의 발생
VB에서는 library function으로 난수 발생 함수를 제공하고 있다. 먼저 Seed를 random하게 제공하는 방법은
"randomize"
라는 statement를 주면 된다. 만약 어떤 특정한 수를 seed로 주기를 원할 때에는
"randomize(특정한 수)"
를 주면 된다. 만약 randomize만 주면 VB가 Timer함수를 이용하여 시각을 seed로 택하는 작업을 한다. Timer 함수는 자정에서부터 현재 시각까지의 시간을 초로 환산하여 준다. Seed를 randomize로 random화 시킨 후 난수 열을 얻는 방법은 "Rnd" statement를 이용하면 된다. "Rnd"는 구간 (0,1) 사이의 난수를 준다. 따라서 특정한 구간 (a,b)의 난수열을 얻는 방법은
a + (b-a)*Rnd
를 이용하면 된다.
2. Monte Carlo Integral
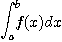 를 난수열을 사용해서 계산하는 방법.
를 난수열을 사용해서 계산하는 방법.
Hit and Miiss Method
i) 가로가 (b-a), 세로가 h인 직 사각형을 그린다.
ii) 구간 (a,b)안에 있는 난수 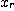 하나와, (0,h) 구간 안의 난수
하나와, (0,h) 구간 안의 난수 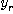 하나를 발생시켜서
하나를 발생시켜서 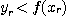 을 만족시키면 Hit 수를 하나 증가시키고, 아니면 Miss 수를 하나 증가시킨다.
을 만족시키면 Hit 수를 하나 증가시키고, 아니면 Miss 수를 하나 증가시킨다.
iii) ii)의 과정을 충분한 횟수 N번 반복한다.
그러면 적분 값은
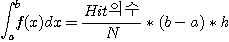
로 추정할 수 있다.
Important Sampling Method
구간 (a,b)안에 있는 난수를 충분한 횟수 N 번 발생 시켜 그 난수 열을 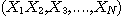 이라 하면 적분 값은
이라 하면 적분 값은
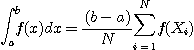
로 계산할 수 있다. 그 이유는 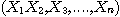 이 진정한 의미에서 난수열 이라면 N 이 매우 클 때
이 진정한 의미에서 난수열 이라면 N 이 매우 클 때 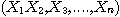 들이 구간 (a,b)에 골고루 분포할 것이며, 따라서 임의의 점이 차지하는 부분 구간의 범위가 (b-a)/N이 될 것이기 때문이다.
들이 구간 (a,b)에 골고루 분포할 것이며, 따라서 임의의 점이 차지하는 부분 구간의 범위가 (b-a)/N이 될 것이기 때문이다.
3. Muilti-Dimensional Integral
다중 적분
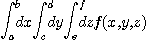
와 같은 적분의 수치값은 단순히 일차원 적분의 algorithm을 이용하여 적분하기에는 매우 어려운 점이 많다. 특히 적분의 하한, 상한들이 일정한 값이 아니라, 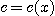 등과 같이 다음에 적분 될 변수의 함수인 경우에는 특히 어렵다. 이럴 때 매우 용이하게 적분할 수 있는 방법이 바로 Monte Carlo Integral이다. 여기서도 importance sampling method를 이용하여 적분하는 방법은 다음과 같다. 구간 (a,b)안에 있는 난수를 충분한 횟수 N 번 발생 시켜 그 난수 열을
등과 같이 다음에 적분 될 변수의 함수인 경우에는 특히 어렵다. 이럴 때 매우 용이하게 적분할 수 있는 방법이 바로 Monte Carlo Integral이다. 여기서도 importance sampling method를 이용하여 적분하는 방법은 다음과 같다. 구간 (a,b)안에 있는 난수를 충분한 횟수 N 번 발생 시켜 그 난수 열을 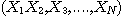 이라 하고, 구간 (c,d)안에 있는 난수를 충분한 횟수 M 번 발생 시켜 그 난수 열을
이라 하고, 구간 (c,d)안에 있는 난수를 충분한 횟수 M 번 발생 시켜 그 난수 열을 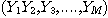 이라 하고, 구간 (e,f)안에 있는 난수를 충분한 횟수 L번 발생 시켜 그 난수 열을
이라 하고, 구간 (e,f)안에 있는 난수를 충분한 횟수 L번 발생 시켜 그 난수 열을 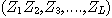 이라 하면 적분 값은
이라 하면 적분 값은
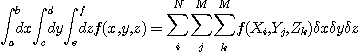
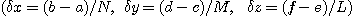
으로부터 계산할 수 있다.
4. 반복법(iteration method)과의 조화
i) Monte Carlo 적분법에서의 정확도의 추정은 난수 발생 횟수와 적분 결과 값의 상관 관계를 구하면 된다. 가령 난수를 100 번 발생 시켰을 때의 적분 값이 9.576이고 1000 번 발생 시켰을 때의 적분 값이 9.432이고, 10000 번 발생 시켰을 때의 적분 값이 9.441이고, 100000 번 발생 시켰을때의 적분 값이 9.447이라면 적분 값이 소수점 이하 2 째자리까지 정확히 구하려면 적어도 난수를 10000 번이상 발생시켜야 적분 값이 제대로 나온다고 추정할 수 있다.
ii)인간이나 computer가 주는 한계 때문에 난수 발생횟수의 최대치가 N 번으로 한정된다면, N 번을 전부를 1 번의 적분 값 추정에 다 사용할 것이 아니라, 횟수를 k로 나누어 난수 발생 횟수가 N'=N/k인 Monte Carlo Intergral을 k 번하여 그 결과 적분 값을 평균하는 것이 더 정확하다. (즉 상대오차가 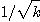 로 줄어들음.)
로 줄어들음.)
따라서 i)과 ii)의 방법을 적당히 조화하는 것이 매우 중요함.
5. Monte Carlo Integral의 구현
이제 VB 프로그램으로 적분 값
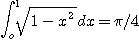
Mpnte Carlo Integral하는 프로그램을 작성해 보자. 여기서는 Hit and Miss method를 사용해 보자. 먼저 이 프로그램을 run하는 과정의 form의 모양을 보면 다음과 같다.
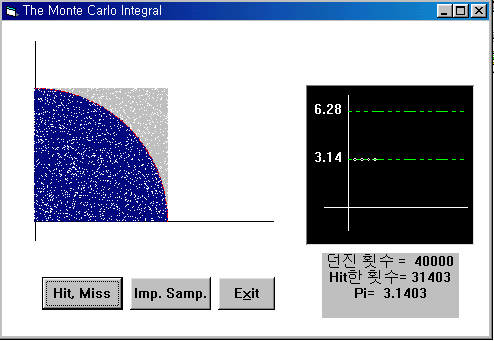
이 그림은 Buffon의 바늘 떨어 뜨리기 프로그램을 구현할 때와 form과 비슷한 형태를 갖고 있다. 이 프로그램의 form file, project file은 실행 file은 각각MonInt.frm, MonInt.vbp, MonInt.exe와 같다.
이제 이 프로그램을 구체적으로 살펴보자. form의 control의 속성 중 Picture Box인 picResult안에 있는 모든 control은 Buffon의 바늘 떨어 뜨리기 프로그램에서의 picResult안에 있던 control의 속성과 동일하므로 생략한다. 이제 나머지 control들을 위한 속성표를 작성해 보자.
객체 | 속성 | 설정 |
form | Name | frmMonInt |
label | Name | lblResult |
line | Name | linXax(x축) |
line | Name | linYax(y축) |
command | Name | cmdHitMiss |
command | Name | cmdImpo |
command | Name | cmdExit |
다음으로 프로 그램 code를 작성해 보자.
먼저 일반 선언부를 보면 변수를 모두 선언한다는
Option Explicit
가 있고, 다음으로 난수 짝을 발생하는 총 횟수를 나타내는 전역 변수, gTotal과 그 중 hit한 수를 나타내는 gIn과 결과 적분 값의 4 배를 나타내는 Pi등이 전역 변수로 선언된다.
Dim gTotal As Long
Dim gIn As Long
Dim Pi As Double
또 lblResult라는 label Box에 결과를 표시할 문자열 변수로 Info를 전역변수로 또 선언한다.
Dim Info As String
또 End Button을 click했을 때는 프로그램을 끝내는 procedure가 있다.
Private Sub cmdExit_Click()
End
End Sub
다음으로 프로그램이 시작되어 form이 뜰 때 gTotal과, gIn을 초기화 하는 프로그램은 다음과 같다.
Private Sub Form_Load()
gTotal = 0
gIn = 0
End Sub
다음으로 Hit and Miss를 구현하는 프로그램은 Hit, Miss라는 button을 click했을 때 시행되는데 그 source code를 이제 살펴보자.
Private Sub cmdHitMiss_Click()
먼저 필요한 변수들을 선언하고
Dim Count As Long
Dim CX, CY As Long
Dim Th As Double
Dim DX, DY As Double
좌표 중심을 원점으로 하는 반경 2000 twib인 1/4 원을 빨간색인 원을 그린다.
"circle (x,y), R, color, 시작 angle, 끝나는 angle"이라는 명령에서 시작 angle=0, 끝나는 angle=pi/2 = 1.5706으로 주면 1/4 원을 그리게 된다.
frmMonInt.Circle (linXax.X1, linXax.Y1), 2000, RGB(255, 0, 0), 0, 1.5706
다음으로 난수 발생의 seed를 바꾸고
Randomize
이제 난수 짝의 발생 횟수를 monitor하는 Count란 변수를 0으로 초기화 하고
Count = 0
Do While 구문을 이용하여 난수 짝을 10000 번 발생시켜 Monte Carlo Integral을 한다.
Do While Count < 10001
난수 발생 횟수를 하나 올리고
Count = Count + 1
이제 0 과 1 사이의 난수 두 개를 발생 시켜 각각 x(DX)와 y(DY)의 짝으로 한다.
DX = Rnd
DY = Rnd
다음으로 이 두수를 제곱하여 더하여 Th라 둔다.
Th = DX * DX + DY * DY
이제 난수 발생횟수를 하나 증가 시키고
gTotal = gTotal + 1
이 두수가 함수의 위에 찍히는 지 아래에 찍기 위해 그림에서 DX와 DY에 해당하는 위치 CX, CY로 구해 보자. 그림에서 반경 2000 twib이 실제 1로 환산되고, 원점의 x 좌표는 그림에서 linXax.X1이므로 CX는
CX = Int(DX * 2000 + linXax.X1)
이 되고 같은 방법으로
CY = Int(linXax.Y1 - DY * 2000)
이 된다. 이제 그림에 난수 발생으로부터 얻은 임의의 점이 주어진 함수 아래에 있는지 없는지를 판단하여
If Th <= 1 Then
있으면 Hit 횟수를 하나 증가시키고
gIn = gIn + 1
Hit한 표시로 QBColor(1)으로 점을 찍고
frmMonInt.PSet (CX, CY), QBColor(1)
Miss했으면
Else
Miss한 표시로 QBColor(7)으로 점을 찍고
frmMonInt.PSet (CX, CY), QBColor(7)
End If
Loop
이제 이런 일을 10000번 했을 때 마다 적분 값을 구하는데 우리가 생각한 가상의 4 각형의 넓이가 1이므로 구하는 적분 값은 1*gIn / gTotal인데 이 값을 4 배하면 Pi 값이 되어야 하므로
Pi = 4 * gIn / gTotal
와 같이 Pi값을 계산한다. 그 결과를 needle program에서와 비슷한 방법으로 picResult에 그림을 그리고, lblResult에 문자열로 표시한다.
picResult.Circle (gTotal / 100 + cyLin.X1, cxLin.Y2 - Int(720 * Pi / 3.141592)), 20, RGB(255, 255, 255)
Info = "던진 횟수 = " + Str(gTotal) + Chr(13) + Chr(10)
Info = Info + "Hit한 횟수=" + Str(gIn) + Chr(13) + Chr(10)
Info = Info + "Pi= " + Str(Pi)
lblResult.Caption = Info
End Sub
연습문제:1. 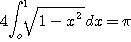 을 이용하여 pi값을 Monte Carlo Intergral의 Important Sampling Method를 이용하여 구하는 source code를 위의 VB프로그램 중 "Private Sub cmdImpo_Click()" procedure에 삽입하라.
을 이용하여 pi값을 Monte Carlo Intergral의 Important Sampling Method를 이용하여 구하는 source code를 위의 VB프로그램 중 "Private Sub cmdImpo_Click()" procedure에 삽입하라.
2. 반경이 1 인 균일한 구형의 강체 내부에 구의 중심과 일치하는 중심을 갖는 모서리의 길이가 1/2인 정육면체를 파 내었다. 이 때 파낸 정육면체의 한 대각선을 중심축으로 하여 이 모양의 관성 모우멘트를 Monte Carlo Integral을 이용해 구하라.
'수학 (Mathematics) > 수치해석학' 카테고리의 다른 글
| 수치계산 프로그램들의 비교[ Comparison of computer algebra systems ] (0) | 2012.11.03 |
|---|---|
| 수치 계산기 wxMaxima (0) | 2012.11.03 |
| 매쓰매티카 사용법 (0) | 2012.11.03 |

