치환적분, 단조함수, 일대일대응함수 이어야만 하는가?

결론은 아니다( 상관없이 된다 )

 

[ 각 함수들의 구간에서 또는 함수끼리의 포함 관계에서 연속이 보장되어야 한다는 것이 포인트 ]

http://kin.naver.com/qna/detail.nhn?d1id=11&dirId=1113&docId=136853309

먼저 치환적분의 원리를 알아야겠죠. 그러면 치환적분을 적용할 수 있기 위한 조건을 찾을 수 있을 겁니다.

 

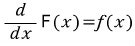인 함수 F를 생각해 봅시다.

튀어나온 조건: F(x)는 연속이고 미분 가능해야 하며 f(x)는 연속이어야 한다.

 

만일 함수 F를 t에 관하여 미분을 하면(단, x=g(t))

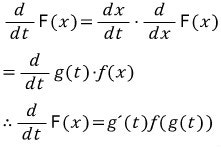
튀어나온 조건: g(t)는 연속이고 미분 가능해야 한다.

그리고 g: t→x에서 함수 g의 치역, 즉 g(t)의 범위가 함수 f의 정의역, 즉 x의 범위 안에 포함되어야 한다.

 

첫 번째 식에서 양 변을 x에 관하여 적분을 하면 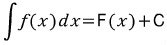가 됩니다.

두 번째 식에서 양 변을 t에 관하여 적분하면.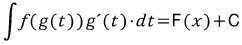

따라서 치환적분 식을 쓸 수 있습니다.

 

한편으로 정적분은 부정적분에 t대신 실수를 대입해서 계산한 결과이기 때문에, 예를들어 위끝과 아래끝이 a와 b이면 둘 다 함수 g의 정의역 안에 들어가야 합니다. 그리고 t의 구간 [a, b]안에서의 함숫값 g(t)가 모두 x의 범위 안에 들어가야 합니다.

한편 t=a일 때 g(t)=g(a)이고, t=b일 때 g(t)=g(b)이므로 정적분에 관한 식은 다음과 같습니다.

 

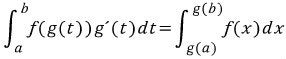
이제 다시 본론으로 돌아가죠.. 서론이 길어졌네요.

 

▷부정적분: f(x)가 모든 정의역에서 연속이고, g(t)는 연속이면서 미분 가능해야 하며, g(t)의 치역이 함수 f의 정의역에 포함되어야 한다.

▷정적분: g(t)가 구간 [a, b]에서 연속이연서 미분 가능해야 하고 g(t)의 치역이 함수 f의 정의역 안에 들어가야 하며 그 치역에 해당하는 구간에서 함수 f가 연속이어야 한다.

 

그런데 서론에서 따지는 과정에서 "일대일 함수"에 관하여 논한 적 없습니다.

실제로 함수를 치환할 때 꼭 일대일 함수일 필요는 없습니다. 책에 그렇게 나와있는건 아마도 오해의 소지가 있을 수 있어서 그런거 아닐까요? 제 개인적인 생각이지만.

그 오해의 소지라는게 다음과 같은게 아닐까 싶습니다.

예를들어 다음 정적분은 두말할 것 없이 반지름의 길이가 1인 반원의 넓이이므로 (π/2)입니다.

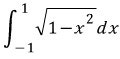
그런데 만일 일대일 함수라는 조건이 빠지면 다음과 같이 계산할 수도 있습니다.

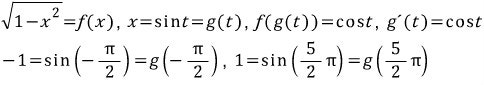
이 식을 이용하여 계산을 하면,

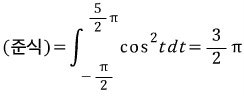처음에 저도 이것때문에 일대일함수라는 조건이 들어간다고 생각을 했는데, 알고보니까 아니더군요. 제가 예전에 봤던 책에서 나온 건데 실수가 있습니다.

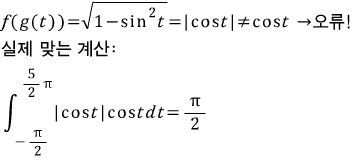
결국 일대일 함수가 아니어도 결과는 맞습니다. 이때 t가 (-π/2)부터 (5/2)π까지 변할 때 g(t)는 일대일 함수가 아니거든요.

 

결론: 일대일 함수가 아니어도 치환적분을 계산할 수 있습니다. 자세한 걸 알고 싶으시면 추가질문 하셔도 좋습니다.