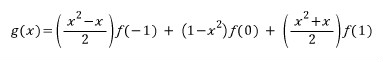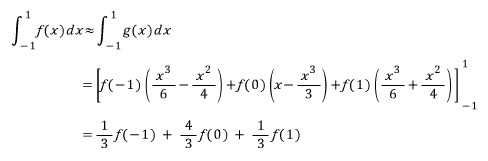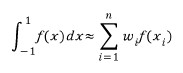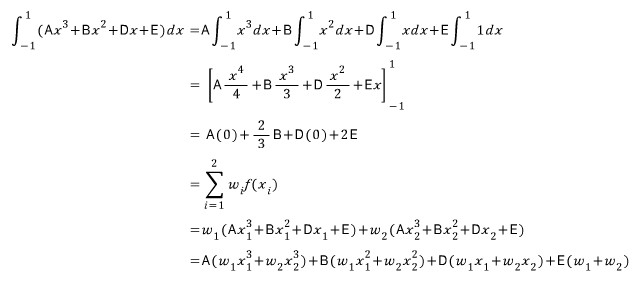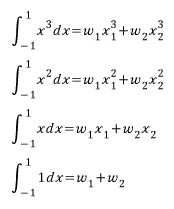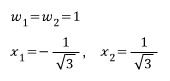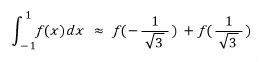선형보간법
라그랑제 다항식 보간법
네빌레의 반복 보간법
뉴튼 다항식에 의한 보간법
은 첨부파일
Gauss quadrature를 배우시다면 그 전에 Newton-Cotes formula 같은 방법은 아실거로 생각되네요.
수치 적분의 기본 가정은 어떤 구간에서 n개의 point와 그에 대응되는 n개의 함수값을 알고 있을 때, 그 n개의 점을 지나는 (n-1)차의 근사다항식으로 식을 가정하여서, 다항식을 적분하는 것입니다.
통상 구간을 [-1, 1]로 두고 시작하는데, 구간이 바뀔 경우에는 적절히 치환 등을 통해 구간을 바꿔서 쓰면 됩니다.
간단한 예로 [-1, 1]사이에서 3개의 점으로 적분값을 구하고자 할 경우 3개의 점을 -1, 0, 1으로 등간격으로 잡게 되고, 그에 대응되는 함수값 f(-1), f(0), f(1)을 사용하여 이 점을 2차는 2차 다항식을 구합니다. 이는 간단히 Lagrangian interpolation 등을 통해
따라서 적분 값은
이 됩니다. (이 방법이 Simpson's rule 입니다.)
이런 결과 들을 종합하여 n차 다항식을 가정하여 구한 적분은
위와 같이 나타낼 수 있습니다. 각 point에 대응되는 함수값과, 그 값에 어떤 weight를 곱한 결과들을 다 더하게 되는 겁니다. 가령 Simpson's rule이라면 point -1, 0, 1에 대해서 그 함수값에 각각 1/3, 4/3, 1/3 이 weight가 되는거구요.
쓸데없이 이런 얘기를 길게 쓴 이유는 다항식으로 가정하는 Newton-Cotes formula는 그 point가 정해져 있다는 것을 말씀드리기 위해서입니다. 통상 등간격으로 정해진 point와 함수값에 대해서 이런 식으로 접근을 한다는 것입니다. 그렇게 point 갯수(n)에 대응되는 (n-1)차 다항식으로 근사시켜서 값을 구합니다.
반면 Gauss-quadrature는 기본적으로 Newton-Cotes formula를 따르는데, 대신 point를 정해진 값이 아니라 변수로 두고서, 적절한 값을 선택하겠다는 것입니다. Newton-Cotes formula에서는 point수가 정해지면 나머지는 그 수에 대응되는 weight를 구하기만 하면 됩니다. 반면에 Gauss quadrature는 point까지 미지수로 두면서 n개의 point와 n개의 weight를 가지고서 다항식을 근사적으로 구합니다. 결국 2n 개의 미지수를 가지는 셈이니, (2n-1)차의 다항식으로 근사시킬 수 있습니다. 단지 n개의 point만을 사용해서요.....
위 식을 그 과정 중에 하나의 예로서 2-point Gauss quadrature를 설명하고 있습니다. 2개의 point와 2개의 weight를 미지수로 두고 있으므로 3차의 다항식으로 가정할 수 있게 됩니다. 따라서 그렇게 가정해서 구한 적분은 3차 이하의 다항식에 대해서는 정확하게 적분값이 맞아야 합니다. 따라서 임의의 3차 다항식에 대해서 그 결과가 정확해야 하므로
가 됩니다. 따라서 A, B, D, E 각 항의 계수를끼리 묶으면
가 되는겁니다.
쓸데없이 식을 늘여쓰긴 했지만 결국 2개의 point와 2개의 weight로 3차 다항식을 구현하였으므로, 2 point Gauss quadrature는 0차, 1차, 2차, 3차 다항식에 대해서 해가 정확하게 일치해야 된다는 조건을 각각 나열한 것입니다.
그리고 중간에 제가 기입해 놓은것처럼 3차에 대해서는 0, 2차에 대해서는 2/3 1차에 대해서는 0 0차에 대해서는 2가 되어야 된다는 조건에서
라는 값이 구해집니다.
최종적으로 2point Gauss quadrature는 다음과 같습니다.
|
'수학 (Mathematics) > 공업수학' 카테고리의 다른 글
| 변수변환법(매개 변수 변환법) (0) | 2012.11.03 |
|---|---|
| 동차비분방정식 , 완전미분방정식 (0) | 2012.11.03 |
| 고차 방정식의 해 구하기 (뉴튼 - 랩슨법, Newton-Rahpson (0) | 2012.11.03 |
| 원뿔곡선 (0) | 2012.11.03 |
| 계수낮추기(계수저하법) , y2 = y1 ∫ ( (e^- ∫ pdx)/y1^2 ) dx (0) | 2012.11.03 |