그린 함수
위키백과, 우리 모두의 백과사전.
수학에서 그린 함수(Green's function)는 미분방정식 을 풀기 위해 사용하는 함수로, 물리학, 공학의 전반에 걸쳐 응용되고 있으며, 특히 물리의 양자장 이론에서 자주 쓰인다. 이 함수는 1830년에 이 방법을 개발한 영국의 수학자 조지 그린 의 이름을 따 명명되었다.
목차[숨기기] |
[편집]정의와 응용
선형 미분 연산자  와 함수
와 함수  가 정의되어 있으며,
가 정의되어 있으며,
을 만족하는  를 찾으라는 문제가 주어졌다고 하자.
를 찾으라는 문제가 주어졌다고 하자.  일 때 해는 제차 상미분 방정식이므로, 비교적 구하기 간단하지만,
일 때 해는 제차 상미분 방정식이므로, 비교적 구하기 간단하지만,  가 조금이라도 복잡해지면 비제차 상미분 방정식이므로 풀기가 어려워진다. 만일, 아래와 같은 성질을 가진 함수
가 조금이라도 복잡해지면 비제차 상미분 방정식이므로 풀기가 어려워진다. 만일, 아래와 같은 성질을 가진 함수  를 찾을 수 있다고 하면,
를 찾을 수 있다고 하면,
(단, (2)에서  는 디랙 델타 함수이다.) 디랙 델타 함수의 성질을 이용해 해를 쓸 수 있다. 해는 다음과 같다.
는 디랙 델타 함수이다.) 디랙 델타 함수의 성질을 이용해 해를 쓸 수 있다. 해는 다음과 같다.
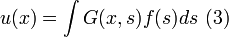
참고 문헌
- Eyges, Leonard, The Classical Electromagnetic Field, Dover Publications, New York, 1972. ISBN 0-486-63947-9. (Chapter 5 contains a very readable account of using Green's functions to solve boundary value problems in electrostatics.)
- A. D. Polyanin and V. F. Zaitsev, Handbook of Exact Solutions for Ordinary Differential Equations (2nd edition), Chapman & Hall/CRC Press, Boca Raton, 2003. ISBN 1-58488-297-2
- A. D. Polyanin, Handbook of Linear Partial Differential Equations for Engineers and Scientists, Chapman & Hall/CRC Press, Boca Raton, 2002. ISBN 1-58488-299-9
반응형
'수학 (Mathematics) > 공업수학' 카테고리의 다른 글
| 비선형미방으로 풀어야 하는데 두 가지에 대해 비례할 경우 (0) | 2012.11.03 |
|---|---|
| 선형미분방정식 vs 비선형미분방정식 (0) | 2012.11.03 |
| 편미분 방정식 (0) | 2012.11.03 |
| 상미분 방정식 (0) | 2012.11.03 |
| 미분 방정식을 하는 이유 (0) | 2012.11.03 |


