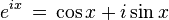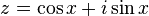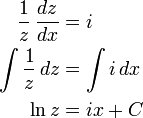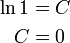원본은 위키백과이고 중간에 약간 식을 추가..
오일러의 공식
오일러의 공식은 수학자 레온하르트 오일러의 이름이 붙은 공식으로, 삼각함수와 지수함수에 대한 관계를 나타낸다. 오일러의 등식은 이 공식의 특수한 경우이다.
오일러의 공식은 다음과 같다. 실수 x 에 대해, 다음이 성립한다.
여기서, e는 자연로그의 밑인 상수이고, i는 제곱하여 -1이 되는(i2 = - 1) 허수단위, sin,cos은삼각함수의 사인과 코사인 함수이다.
x에 π를 대입하여, eiπ + 1 = 0 이라는 오일러의 등식을 구할 수 있다.
목차[숨기기] |
역사
오일러 공식은 1714년 로저 코츠가 다음과 같은 형태로 처음 증명하였다.
지금과 같은 모양의 오일러의 공식은 1748년 오일러가 무한급수의 좌우 극한값이 같음을 증명하면서 발표되었다. 그러나 로저와 오일러 모두 이 공식이 지닌 '복소수를 복소평면 위의 하나의 점으로 볼 수 있다'는 기하학적 의미를 눈치채지는 못하였고, 이것은 약 50년이 지난 후에나 발견되었다. 오일러는 현재의 교육과정에서 보다 훨씬 이른 시기에 학생들에게 복소수를 가르쳤다. 그의 기초 대수학 교재인 대수학 원론(Elements of Algebra)에 보면 교재의 거의 맨 앞부분부터 복소수를 도입하고 있고 교재 전체를 통틀어 자연스럽게 사용하고 있다.
3DMP engines
3D그래픽스 물리 수학, 프로그래밍 GPU Shader 게임엔진 알고리즘 디자인패턴 matlab etc..
이 줄친 사이부분만 추가..
x <= pi/2
90도에 의하여 cos(pi/2) = 0 , sin(pi/2) = 1
e^i(pi/2) = 0 + i*1
i = e^i*pi/2
i^i = (e^i*pi/2)^i = e^i*(pi/2)i = e^i*i*(pi/2)= e^-(pi/2) -> 실수가 된다
증명
[편집]테일러 급수를 이용한 방법
테일러 급수에 따라 실수 범위에서 다음의 식이 성립한다.
이때 x가 복소수일 때에 앞의 무한급수를 각각의 함수로 정의한다. 그러면
가 된다.
[편집]미분 계산을 이용한 방법
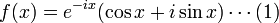 라면,
라면,
 (단, C는 상수)
(단, C는 상수)
(1)에 x = 0을 대입하면,
- f(0) = 1

- e − ix(cosx + isinx) = 1
- eix = (cosx + isinx)
[편집]미적분을 이용한 방법
다음과 같은 복소수 z를 생각하자:
양변을 x에 대해 미분하면:
i2 = - 1이므로:
양변을 적분하면:
(여기에서 C는 적분 상수이다.)
이제 C = 0이라는 것을 증명한다. x = 0일 경우를 계산해보면
따라서
따라서 다음과 같은 식이 성립한다:
[편집]미분방정식을 이용한 방법
함수 g(x) 를 다음과 같이 정의한다.
- g(x) = eix
허수단위 i 는 상수이므로 g(x)의 도함수와 이계도함수는 다음과 같다.
이로부터
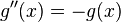 또는
또는 라는 2차 선형 미분방정식이 만들어지고,
라는 2차 선형 미분방정식이 만들어지고,
일차 독립인 두 해가 발생한다.
한편, 차수가 같은 미분방정식의 어떤 선형 결합도 해가 될 수 있으므로 위의 미분방정식의 일반적인 해는 다음과 같다.

- (A와 B는 상수)
그리고 여기에 함수 g(x) 의 초기 조건
 을 대입하면,
을 대입하면,
곧,
이므로
 이다.
이다.
[편집]cis 함수
cis 함수 또는 복소 지수 함수는 오일러의 공식으로부터 바로 유도되는 함수로, 다음과 같이 정의된다.
이 함수는 푸리에 변환이나 페이저 등에서 복소수와 관련된 연산을 할 때 흔히 사용된다.
'수학 (Mathematics) > 미적분학' 카테고리의 다른 글
| 부분분수 (0) | 2012.11.03 |
|---|---|
| 미분공식3개 (tan^-1(x))' , ∫1/(1+x^2) dx , ∫1/(a^2+x^2) dx (0) | 2012.11.03 |
| 심슨의 법칙 (0) | 2012.11.03 |
| 2변수에 대한 테일러급수 정리 (0) | 2012.11.03 |
| 벡터 외적 기본공식 (0) | 2012.11.03 |