
3DMP engines
3D그래픽스 물리 수학, 프로그래밍 GPU Shader 게임엔진 알고리즘 디자인패턴 matlab etc..
결론적으로 이것은 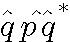 인 결과 즉 사원수3개의 곱으로(또는 p 가 w=0 인 벡터여도 상관없다) 나온 결과들을
인 결과 즉 사원수3개의 곱으로(또는 p 가 w=0 인 벡터여도 상관없다) 나온 결과들을
행렬로 옮겨놓은것이다
이하내용은 지금은 알수 없는 어디선가 퍼온자료
쿼터니언은 복소수의 확장으로 i, j, k 3개의 허수와 w, x, y, z 4개의 실수부로 이루어져 있다.
즉 하나의 스칼라와 3개의 벡터 ==> 4개의 구성 요소로 이루어진 복소수를 말한다.
허수 i, j, k는 i * i = -1의 성질을 가진다.
| = w + xi + yj + zk |
= sq + vq | |
= (sq , vq) | |
= [ w , (x, y, z) ] |
여기서 w는 스칼라 v = (x, y, z)는 벡터이다.
쿼터니언 크기 ||q|| = Norm(q) = sqrt(w2 + x2 + y2 + z2)
단위 쿼터니언 성질 w2 + x2 + y2 + z2 = 1
단위 쿼터니언은 (x, y, z)요소를 임의의 축, w요소를 회전 각도로 하여 4차원 공간에 표현 할 수 있다.
그림으로 간단하게 표현 하면 벡터 축 A를 중심으로 회전하는 θ는
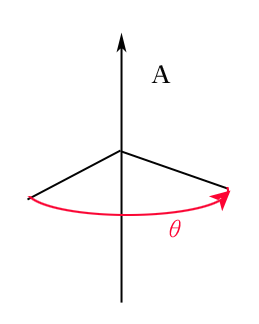
사원수를 이용한 벡터 회전 변환
벡터 p를 사원수 q로 회전할 때 공식과 행렬에 대한 변환은 다음과 같다.
| = | | | 1 - 2Y2 - 2Z2 2XY + 2ZW 2XZ - 2YW | 2XY - 2ZW 1 - 2X2 - 2Z2 2YZ + 2XW | 2XZ + 2YW 2YZ - 2XW 1 - 2X2 - 2Y2 | | | | | | | |
쿼트니언을 행렬 변환하는 함수
//----------------------------------------------------------------------------- //예전 다이렉트X 버전에 d3dmath.cpp 파일에 있는 소스이다. //----------------------------------------------------------------------------- VOID D3DMath_MatrixFromQuaternion( D3DMATRIX& mat, FLOAT x, FLOAT y, FLOAT z, FLOAT w ) { FLOAT xx = x*x; FLOAT yy = y*y; FLOAT zz = z*z; FLOAT xy = x*y; FLOAT xz = x*z; FLOAT yz = y*z; FLOAT wx = w*x; FLOAT wy = w*y; FLOAT wz = w*z;
mat._11 = 1 - 2 * ( yy + zz ); mat._12 = 2 * ( xy - wz ); mat._13 = 2 * ( xz + wy );
mat._21 = 2 * ( xy + wz ); mat._22 = 1 - 2 * ( xx + zz ); mat._23 = 2 * ( yz - wx );
mat._31 = 2 * ( xz - wy ); mat._32 = 2 * ( yz + wx ); mat._33 = 1 - 2 * ( xx + yy );
mat._14 = mat._24 = mat._34 = 0.0f; mat._41 = mat._42 = mat._43 = 0.0f; mat._44 = 1.0f; } |
행열을 쿼트니언으로 변환하는 함수
VOID D3DMath_QuaternionFromMatrix( FLOAT& x, FLOAT& y, FLOAT& z, FLOAT& w, D3DMATRIX& mat ) { if( mat._11 + mat._22 + mat._33 > 0.0f ) { FLOAT s = (FLOAT)sqrt( mat._11 + mat._22 + mat._33 + mat._44 );
x = (mat._23-mat._32) / (2*s); y = (mat._31-mat._13) / (2*s); z = (mat._12-mat._21) / (2*s); w = 0.5f * s; } else {
} FLOAT xx = x*x; FLOAT yy = y*y; FLOAT zz = z*z; FLOAT xy = x*y; FLOAT xz = x*z; FLOAT yz = y*z; FLOAT wx = w*x; FLOAT wy = w*y; FLOAT wz = w*z;
mat._11 = 1 - 2 * ( yy + zz ); mat._12 = 2 * ( xy - wz ); mat._13 = 2 * ( xz + wy );
mat._21 = 2 * ( xy + wz ); mat._22 = 1 - 2 * ( xx + zz ); mat._23 = 2 * ( yz - wx );
mat._31 = 2 * ( xz - wy ); mat._32 = 2 * ( yz + wx ); mat._33 = 1 - 2 * ( xx + yy );
mat._14 = mat._24 = mat._34 = 0.0f; mat._41 = mat._42 = mat._43 = 0.0f; mat._44 = 1.0f; } |
'수학 (Mathematics) > 3D수학' 카테고리의 다른 글
| [2D] 고속 선그리기, 브레슨햄 알고리즘 [영상강의 및 설명] (0) | 2012.11.02 |
|---|---|
| 점이 다각형 내부에 있는지 외부에 있는지의 판정 (0) | 2012.11.02 |
| [2D] 평행이동 타원과 선분의 교차판정 (0) | 2012.11.02 |
| 타원 그리기 (0) | 2012.11.02 |
| 원과 선분의 충돌 (0) | 2012.11.02 |
