프로그래밍에 있어서는 기하는
사실적으로 쉬운 부분이다.
그러나 대부분(?)의 인간들은 기하에 대한 문제를
어렵게 생각한다. 물론 나도 마찬가지이다.
기하는 여러 경우로 나눠서 생각해보아야 하기 때문이다.
그러면 우선적으로 기본부터 알고가자.
========== 다각현의 면적 ===========
수올을 한다면 대부분은 알고있을 것이다.
다각형의 각 꼭지점의 좌표가 시계방향순으로 했을경우에
(x1,y1), (x2,y2), ... , (xn,yn)이라 하자. (-> n각형)
(혹은 반시계방향도 괜찮다. 또, 삼각형일때는 순서는 상간없다.)
면적 S는 다음과 같이 구한다.
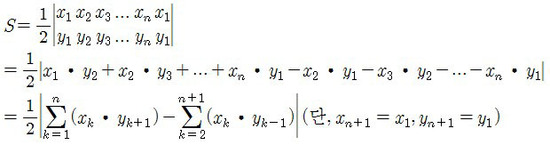
이를 흔히 사선식이라 부른다.
증명은 알아서 해보길 바란다.
====== 시계 및 반시계 방향 확인 ======
어느 세 점, (x1,y1), (x2,y2) (x3,y3), 이 있다하자.
이때 이 세 점을 순서대로 이어서 선을 그을 때 이 선이
시계방향으로 돌아가는가, 반시계방향으로 돌아가는가를 아는 것 이다.
위의 사선식을 이용하면 쉬게 구할 수 있다.
S = 1/2 |x| 라 해보자. (이 경우에서는 n=3일 때이다.)
i) x<0 ; 이는 시계방향을 의미이다.
ii) x=0; 이는 일직선 상에 세 점이 놓여있음을 의미한다.
iii) x>0; 이는 반시계방향을 의미한다.
증명은 역시 알아서 해보길 바란다.
========= 선분 교차 =========
선분교차의 여부에 관한것은 내가 이 블로그에 올려놨으니 그 설명으로도 충분히 이해가 가길 바란다.
=========== 점의 위치 ==========
어떤 점 (x0,y0) 이 있다 해보자.
그리도 n각형의 도형 (x1,y1) ~ (xn,yn)있다 하자. (n≥3)
그럴때 (x0,y0)이 위의 도형안에 있는지,
도형 위에 있는지, 또 도형 밖에 있는지를 판별 해 보려고 한다.
점이 도형위에 있는지를 판별하는것은 문제가 되지 않는다.
임의의 한 변과 주어진 점으로 사선식을 돌렸을때 0이 나와야하며
점의 좌표범위가 (xi,yi), (x(i+1),y(i+1))의 내부에 위치하기만 한다면
선분위에 그 좌표가 있는셈이다. (물론 방법은 조금 달라도 된다.)
그럼 나머지의 경우를 알아보자.
방법은 간단하다.
(x0,y0)에서 오른쪽으로 직선을 그어보자. ((x0,y0) - (∞,y0) 연결)
그 선분과 도형과의 교점갯수를 세어봤을때
짝수이면 점은 도형 바깥에 위치하는 것이며
홀수이면 점은 도형 안쪽에 위치하게 되는 셈이다.
셀 때에는 그저 각 선분마다 그 반직선과 만나면 갯수를 증가시켜주면 된다.
그러나 교점을 셀 때에는 어떤 경우는 세어야 하며
어떠한 경우는 세지 말아야 하는 경우가 생기게 된다.
다음 그림을 봐보자.
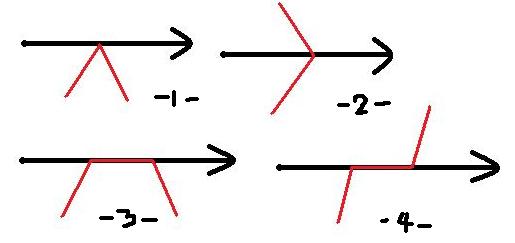
1,3번과 같은 경우는 만나지 않은것으로,
2,4번과 같은 경우는 1번 만난것으로 체크를 해 쥐야 한다.
그러므로
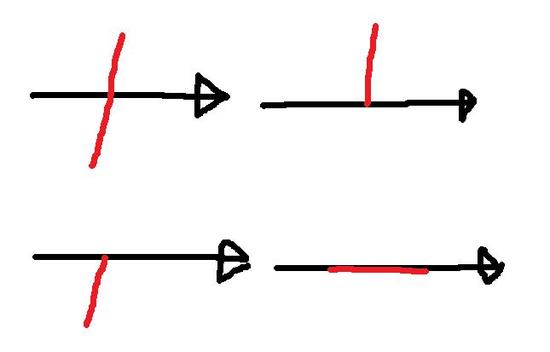
위와같은 경우에서 첫줄일 경우에만 한번 체크해 주면 되겠다.