http://sayzy.blog.me/70080729572
벡터의 내적
내적의 특성
| ▣ 만약 두 벡터가 UㆍV = 0 라면, U와 V는 직각이다. |
| ▣ 만약 두 벡터가 UㆍV > 0 라면, 두 벡터 간의 각도는 90도 보다 작다. |
| ▣ 만약 두 벡터가 UㆍV < 0 라면, 두 벡터 간의 각도는 90도 보다 크다. |
가장 중요한 것은 두 벡터의 내적은 그 결과가 항상 스칼라라는 것입니다. 이 때문에 스칼라 적이라고도 하며 점곱 이라고도 불립니다.
공간상에 임의의 두 벡터 A, B가 있을때..


두 벡터 사이의 각 구하기
우리는 위의 공식을 이용하여 두 벡터간의 각을 알아낼수가 있습니다.
![]()
위 식이 성립됩니다.
코싸인 세타 값을 M이라고 한다면..
![]() 라는 라디안 값을 얻을 수 있습니다.
라는 라디안 값을 얻을 수 있습니다.
투영 벡터
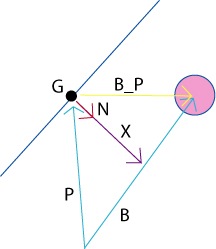
우리는 여기서 어느 한 면에서의 점(G)와 원 사이의 거리를 알고 싶습니다.
그러려면 B_P의 투영 벡터인 X벡터의 스칼라 값을 구하여야 됩니다.
원점에서부터 오는 벡터 P가 있습니다.
그리고 마찬가지로 원점에서부터 오는 벡터 B가 있습니다.
B_P는 B벡터 - P벡터를 한 벡터입니다.
벡터 X의 길이를 s라 하면 s = ![]() 가 됩니다.
가 됩니다.
B_P벡터와 점(G)의 노말 벡터인 N과 내적을 하게 된다면...
내적 값은 N은 길이가 1이므로 이것도 역시 ![]() 가 되게 됩니다.
가 되게 됩니다.
결과를 보면 X의 스칼라 값 s와 N의 내적 값이 같다는걸 보게 됩니다.
따라서 길이가 1인 벡터 N과 B_P의 내적값은 X벡터의 스칼라 값인 길이가 됩니다.
여기에 ![]() x N벡터를 하면 크기와 방향을 가지는 투영 벡터인 X벡터가 나오게 됩니다.
x N벡터를 하면 크기와 방향을 가지는 투영 벡터인 X벡터가 나오게 됩니다.
투영벡터에 관한 정보는 아래 사이트에서 보고 글을 올린 것이니 이해가 안되시면 링크를 따라가셔서 보시면 됩니다.
http://wibler.egloos.com/3574643
벡터의 외적
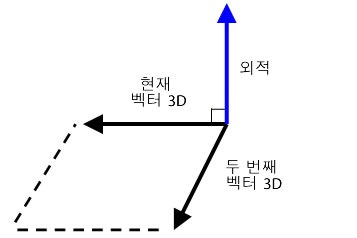
공간상에 임의의 두 벡터 A, B가 있을때..

벡터의 내적이 두 벡터간의 사잇각을 나타내는 스칼라임에 비하여 벡터의 외적은 두 벡터에 모두 수직한
벡터를 결과 값으로 받는다는 점 때문에 크로스곱 또는 벡터적이라고도 합니다.
벡터 A와 B를 포함하는 평면에는 수직인 두개의 방향인 위쪽과 아랫쪽이 있습니다.
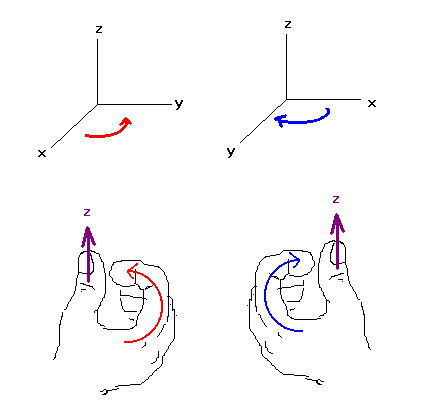
위 그림과 같이 오른손 법칙이나 왼손 법칙으로 두 벡터의 외적 벡터인 z 방향을 알아 낼수가 있습니다.
[출처] 벡터의 내적과 외적 < 5 >|작성자 테라
'수학 (Mathematics) > 3D수학' 카테고리의 다른 글
| 두직선의 교점 (0) | 2012.11.02 |
|---|---|
| 사각형 무게중심 (0) | 2012.11.02 |
| 한 축에 대한 기저 생성 (0) | 2012.11.02 |
| 간단하고 안전한 방향전환 행렬 구하기, 직교 기저 벡터의경우 (0) | 2012.11.02 |
| 점과 직선/반직선/선분과의 거리 (0) | 2012.11.02 |
