점과 직선/반직선/선분과의 거리

출처: http://www.gamza.net

 

copyrightⓒ playUs [2003년 04월 19일]

 

1. 정사영(투영) 벡터

 

 

 

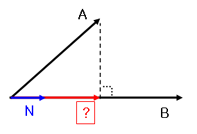
벡터A를 벡터B에 투영한 벡터[?]는 다음과 같이 표현됩니다.[?] = ( 벡터A를 벡터B에 투영한 길이 ) N 
(N : B방향 단위벡터)벡터A를 벡터B에 투영한 길이는 내적을 이용하면 구할 수 있고....
( 벡터A를 벡터B에 투영한 길이 ) = |A|cos@ = A • B / |B|또, B방향 단위벡터는 N은 아래처럼 구해지니....N = B / |B|결국 벡터A를 벡터B에 투영한 벡터[?]를 다시 표현하면 아래와 같이 됩니다.[?] = (A•B/|B|) (B/|B|) = ((A • B)/(|B|*|B|)) B = ((A•B)/(B•B)) B
2. 점과 직선과의 거리
점과 직선의 수직거리는 점에서 직선에 내린 수선(벡터H)의 크기입니다.

 

 

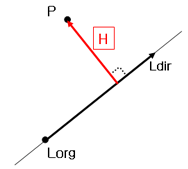
P : 거리를 알고 싶은 점
Lorg : 직선상의 임의의 한점
Ldir : 직선의 방향벡터

 

 

이때 벡터H는 아래그림과 같이 구할수 있죠.

 

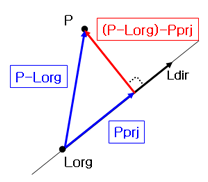
Pprj : 벡터(P-Lorg)를 Ldir에 투영한 벡터

Pprj는 벡터(P-Lorg)를 Ldir에 투영한 투영벡터입니다.
저 위의 투영벡터 공식을 적용해보면...

Pprj = (((P-Lorg)•Ldir)/(Ldir•Ldir)) Ldir최종적으로 벡터 H를 정리하면 다음과 같이 됩니다.H = (P-Lorg) - Pprj = (P-Lorg) - (((P-Lorg)•Ldir)/(Ldir•Ldir)) Ldir식은 길지만 따져보면 상당히 값싼 연산임을 알수 있습니다.
무엇보다도 이 식의 최대 장점은 단위벡터가 필요없다는 것입니다.
벡터를 정규화할 필요가 없으니 보기보다는 훨씬 값싼 연산이라 할수 있죠.

3. 점과 반직선과의 거리

 

 

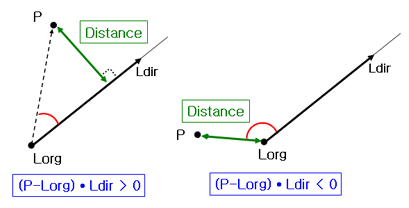
P : 거리를 알고 싶은 점
Lorg : 반직선의 시작점
Ldir : 반직선의 방향벡터

위 그림에서 보듯, 점이 반직선의 시작점보다 뒤쪽(Ldir방향기준)에 있을 경우에 점과 반직선의 거리는 그냥 |P-Lorg|로 구해집니다.

4. 점과 선분과의 거리
벡터A를 벡터B에 투영한 벡터Aprj는 벡터B에 스칼라 값 ((A • B)/(|B|*|B|))을 곱한 벡터입니다.
따라서 계수가 되는 ((A • B)/(|B|*|B|)) 의 크기에 따라 아래와 같이 구분될 수 있습니다.

 

 

 

 

 

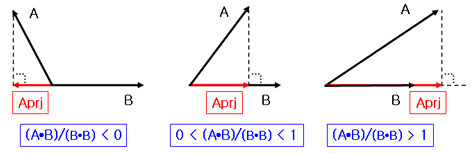
이것을 이용하면 다음 그림과 같이 점(P)과 선분(S0,S1)의 거리를 구할수 있습니다.

 

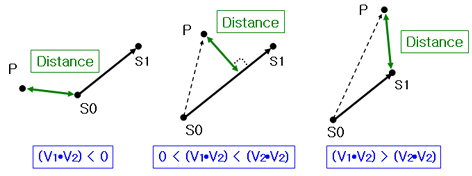
P : 거리를 알고 싶은 점
S0,S1 : 선분을 이루는 두점
V1 : S0에서 P를 향하는 벡터
V2 : S0에서 S1을 향하는 벡터

사실 점과 반직선의 거리는 위에서 세번째 경우를 두번째 경우로 대치시킨것 뿐입니다.