
선 개념 : 원 순열의 반대말은 직순열이다

위 A, B, C 는 보기에는 달라 보이지만 돌려 보면 모두다 같다
즉 원순열 기준으로는 모두다 같다고 본다 (돌렸을때 같으면 같다고 보는것이 원순열, 특정 기준 없이)
주의 : 원순열에선 보기엔 A 가 위에 있을지라도 맨 위에 있다 옆에 있다 그런 개념이 없다, 특정 기준 없이는
직순열과 원순열의 차이는 자리마자 고유번호가 있다인데 이것은 특정 원소를 기준으로 자리를 매길 수 있다는 말입니다
아래 것은 왼쪽이 첫번째 것이라고 특정 기준을 잡은것임으로 직순열이다
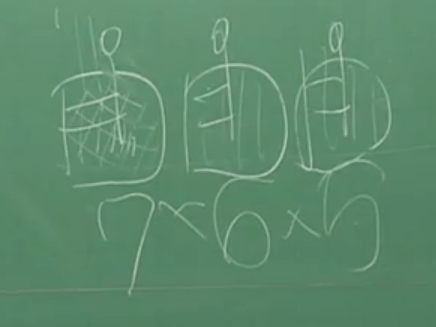
하지만 원순열은 고유번호가 없다, 돌려도 같기 때문
그래서 원순열을 풀때는 기준을 잡고 직순열로 바꿔서 푼다
즉 고유번호 엇는 것을 고유번호 있게 만드는 것이 첫번째 과정이다
=> 원순열에 누군가 한명이 앉으면 그때부턴 기준이 생기게 됨으로 원순열이 아닌 직순열이 된다
첫번재 앉은 사람 왼쪽 또는 오른쪽에 누구를 앉힐 지 정할 수 있는 기준이 되는사람이 앉았음으로
문제 1)
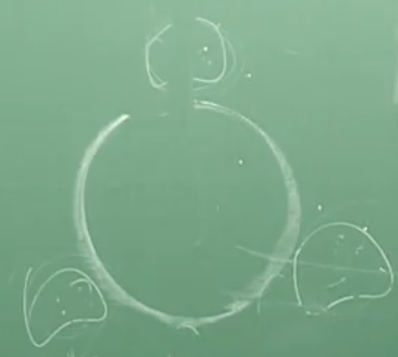
이런 볼품 없는 원탁의자가 있다(그림은 저모양 일지라도 의지는 모두다 같고 구분 할수 없다 가정한다)
이때 첫번째 사람이 앉는 경우의 수는?
답 = 1가지 , 3가지가 아닌데 왜냐면 원순열에서는 돌려도 같기 때문에 처음엔 어떤 기준이 없어서 첫번째 앉는 사람이 어디에 앉든 모두다 같은 경우가 됨으로, 즉 어디에 앉든 다 똑같다( 기준이 애초에 없었음으로 1명이 앉기 전까진)
문제 2)
문제 1 에서 모두다 앉는 경우의 수는?
답 1 * 2! 인데
1명이 앉고 나머지 2명이 앉는 경우의 수임으로 직순열(Permutation) 로 풀면 된다
문제 3)
6명이 원탁에 앉는 경우의 수는?
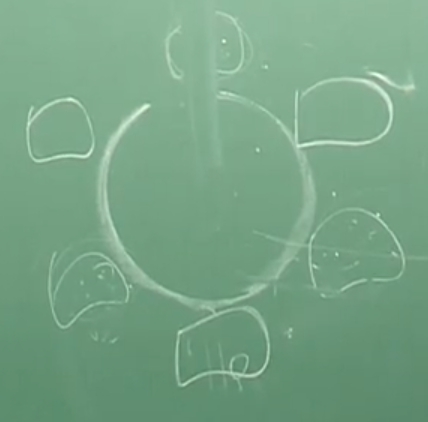
답 = 1 * 5!
n 명이 원탁에 둘러 앉는 경우의 수는?
문제)
A, B 를 포함한 6명이 있는데
A, B 가 이웃하여 앉는 경우의 수를 구하시오
이땐 순열 top 5중
A, B 를 주머니에 넣고 하나라 생각한 후 풀면 됩니다
그래서 우선 총 개수는 5개라 생각하면
1 * 4!
그리고 주머니에 있는 것 2! 을 곱하면
답 = 1 * 4! * 2!
문제 )

A, B 가 마주보며 앉는 경우의 수는?
원으로 생각하면 어려우니깐 일단 기준을 잡아야 한다
즉 A 를 먼저 앉힌다음 생각해보면
A 를 앉히는 경우의 수 1 가지 , 앉히면 직순열이 됨
그런데 그리고 B 가 앉는 경우의 수 1 가지 왜냐면 A 의 반대편아 앉아야 함으로
여기까진 1 * 1 이 된다 그런다음
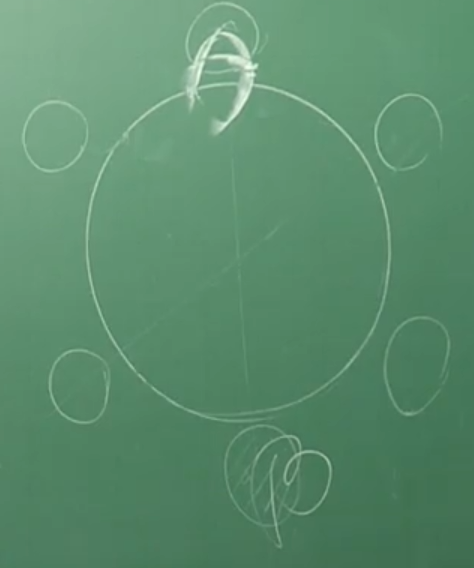
그림 처럼 4자리에 나머지 4명이 앉으면 됨으로
4!
A 가 처음 앉을때 원을 돌아가면서 앉을때도 고려해야 하는것 아닌가? 라고 생각 할수 있지만
원순열에서 A 가 앉음과 동시에 직순열이 되었음으로 이건 이미 고려 대상에선 끝
답 = 1 * 1 * 4!
'수학 (Mathematics) > 확률과통계' 카테고리의 다른 글
| 조합 Top5 (1) (0) | 2023.01.06 |
|---|---|
| 조합 (Combination) (0) | 2023.01.06 |
| 순열 Top5 간단 정리 (0) | 2023.01.06 |
| 조합(combination) (0) | 2012.11.02 |
| 순열 permutation (0) | 2012.11.02 |
