순열 : N 명중에서 R 명을 뽑는 수, 하지만 줄을 세운다
조합 : N 명중에서 R 명을 뽑는 수, 하지만 줄을 세우진 않는다 = 순서 상관 없다 = 즉 뽑는 Action 만 따진다
= 선택하는 경우의 수로 말하기도 함 ex) 10명중에서 5명을 선택하는 경우의 수
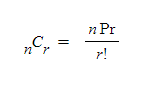
이렇게 되는데
n명중에 r명을 뽑아 줄을 세운다음 줄 세운것을 취소하면 n명 중에서 r 명을 뽑기만 하는것이 된다
다른 말로
순열 nPr 이란 얘기는 n명중에서 r명을 뽑고(여기까지가 nCr ) 다음 그 이후 줄까지 세운 것을 말한다
ex) 10 명중에서 3명을 줄을 세우는 방법의 수는?
10C3 = 10P3 / 3! = 120
콤비네이션은 Permutation 으로 풀어서 푸는것이 좋다
ex) 서로다른 5권의 책이 있는데 그 중 2권을 책을 가지고 가고 싶을때?
5C2 = 5P2 / 2! = 10
외우편 편합 조합들
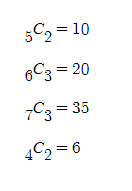
문제 )
100명이 있는데 도시락이 만원이다
100명의 도시락을 사려 했더니 98만원 밖에 없다
이때 98명을 뽑는 경우의 수는?
100C98 = 100P98 / 98!
그런데 계산하기 너무 많다 이럴때
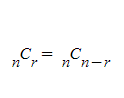
단) n은 r 보다 크거나 같다는 조건이 있습니다
nCr = nC(n-r) 과 같다는 조합의 성질이 있다 (계산해보면 같다는 것을 알수 있습니다)
즉 100C98 = 100C2
100*99/2 = 4950
[특징]
0! = 1
nP0 = 1 (약속임 이건 그냥 정의)
nC0 = 1 , n 명중에 한명도 안뽑은 것도 개수를 쳐서 1이라 함
nP1 =n
nC1 = n
그래서 아래와 같은 특성이 생기게 됩니다
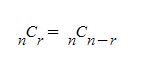
이 성질을 잘 생각하면서 보면 4C2 를 기준으로 대칭이 된다는 것을 알 수 있습니다
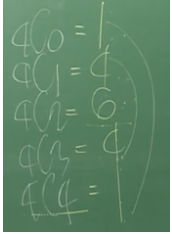
'수학 (Mathematics) > 확률과통계' 카테고리의 다른 글
| 원 순열 (0) | 2023.01.06 |
|---|---|
| 조합 Top5 (1) (0) | 2023.01.06 |
| 순열 Top5 간단 정리 (0) | 2023.01.06 |
| 조합(combination) (0) | 2012.11.02 |
| 순열 permutation (0) | 2012.11.02 |
