상미분 방정식( ordinary differential equation)은 미분 방정식의 일종으로, 구하려는 함수가 하나의 독립 변수만을 가지고 있는 경우를 가리킨다.
y=x+1
독립변수=x, 종속변수=y
[ 정의 ]
1계 미분방정식의 형태가 dy/dx = g(x)h(y) 꼴 일때를
변수분리형 미분방정식 이라 한다
g(x)h(y) : 각각 x, y 의 함수
꼴 일 때
변수분리형 미분방정식이라 한다.
상미분방정식의 일종인 변수분리형 방정식
 => 식에서 y'(or y)와,x(or f(x)) 를 좌,우변으로
=> 식에서 y'(or y)와,x(or f(x)) 를 좌,우변으로 - 각각 분리 시킨다
위 식은 아래와 같이 대수적 조작을 통해 변환할 수 있다.
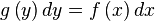 => 이렇게 y(or dy),따로 x(or dx) 분리
=> 이렇게 y(or dy),따로 x(or dx) 분리- f(x)를 x에 대하여 풀이
위의 식을 변수분리형방정식이라 하고, 양변을 적분하면 값을 손쉽게 구할 수 있다.
이렇게 분리한후 양변을 적분한 다음
y=x 의 꼴로 풀면 이것이 상미분 방정식의 해가 된다
http://cafe.naver.com/mathematicians.cafe?iframe_url=/ArticleRead.nhn%3Farticleid=19&
반응형
'수학 (Mathematics) > 공업수학' 카테고리의 다른 글
| 미분 방정식을 하는 이유 (0) | 2012.11.03 |
|---|---|
| 혼합물이 녹는 속도 (0) | 2012.11.03 |
| 어떤 물체의 온도가 주변온도까지 떨어지는 시간은? (0) | 2012.11.03 |
| 적분인자를 이용한 미분 방정식을 완전미분방정식으로 변환하여 해를 구하기 (0) | 2012.11.03 |
| 완전미분방정식과 완전 미분방정식으로 바꿀 수 있는 적분인자, 적분상수를 붙이지 않는 이유 (0) | 2012.11.03 |

