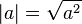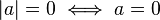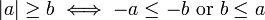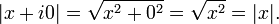절대값의 성질

2012. 11. 2. 21:17

절대값

위키백과, 우리 모두의 백과사전.

이 문서의 제목을 절댓값(으)로 바꾸자는 제안이 있습니다.
토론 문서에서 의견을 나누어 주세요.

수학에서 절댓값이란, 어떤 실수에서 부호를 제거한 값을 말한다. 예를 들어, 3과 -3의 절댓값은 둘 다 3이 된다.

또한, 복소수, 사원수, 벡터 등에 대해서도 절댓값을 일반화시킬 수 있다.

[편집]실수

절대값 함수

어떠한 실수 a의 절대값은 $|a| \,$ 로 표기하며, 다음과 같이 정의된다.

$|a| := \begin{cases} a, & \mbox{if } a \ge 0 \\ -a, & \mbox{if } a < 0. \end{cases}$

정의에 따라, 이 값은 양수나 0이 될 수는 있지만, 음수는 절대 될 수 없다. 그리고 다음의 정리들이 성립한다.

$|a| = \sqrt{a^2}$

$|a| \ge 0$

$|a| = 0 \iff a = 0$

$|ab| = |a||b|\,$

$|a+b| \le |a| + |b|$

$|-a| = |a|\,$ (대칭성)

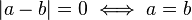
$|a - b| = 0 \iff a = b$

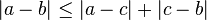$|a - b| \le |a - c| +|c - b|$ (삼각부등식)

$|a/b| = |a| / |b| \mbox{ (if } b \ne 0) \,$

$|a-b| \ge |a| - |b|$

또한, 다음 식은 유용하게 사용된다.

$|a| \le b \iff -b \le a \le b$

$|a| \ge b \iff -a \le -b \mbox{ or } b \le a$

이 식을 이용하면 절대값이 들어간 부등식을 쉽게 풀 수 있다.

$|x-3| \le 9$

$\iff -9 \le x-3 \le 9$

$\iff -6 \le x \le 12$

[편집]복소수

복소수에서는 값들의 크기 비교가 불가능하기 때문에^[1], 실수에서의 정의를 쓸 수 없다. 대신, 앞에서의 성질 중 하나인

$|a| = \sqrt{a^2}$

를 이용할 수 있다.

임의의 복소수

$z = x + yi\,$

에 대해, 절댓값 $| z | ,$ 는 다음과 같이 정의된다.

$|z| := \sqrt{x^2 + y^2}.$

이렇게 정의하면, 앞의 절대값의 성질이 모두 성립하며, 특히 이 정의는 z가 실수일 때에도 성립하게 된다.

$|x + i0| = \sqrt{x^2 + 0^2} = \sqrt{x^2} = |x|.$

이때 피타고라스의 정리에 따라 절대값은 원점과 복소수 사이의 거리를 의미하게 된다. 더 일반적으로, 두 복소수 사이의 거리는 복소수의 차의 절대값이 된다.

저작자표시 비영리 동일조건

'수학 (Mathematics) > 고,중학 수학 및 개념' 카테고리의 다른 글

극선의 방정식 (0)	2012.11.02
치환적분 (0)	2012.11.02
조립제법 (0)	2012.11.02
번분수 (0)	2012.11.02
산술평균, 기하평균, 조화평균 사이의 부등식과 그 증명 (0)	2012.11.02

3DMP

절대값의 성질

절대값

목차

[편집]실수

[편집]복소수

'수학 (Mathematics) > 고,중학 수학 및 개념' 카테고리의 다른 글

+ Recent posts

티스토리툴바