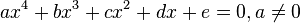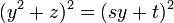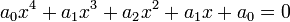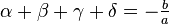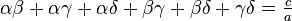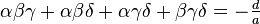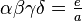사차 방정식

2012. 11. 2. 21:14

사차 방정식

위키백과, 우리 모두의 백과사전.

4차함수의 그래프

사차 방정식이란, 최고차항의 차수가 4인 다항 방정식을 뜻한다. 일반적인 모양은

$ax^4+bx^3+cx^2+dx+e=0 , a\ne 0$

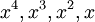와 같다. 여기에서 $a, b, c, d$ 는 각각 $x^4 , x^3 , x^2, x$ 의 계수라고 한다. $e$ 는 상수항이라고 부른다.

[편집]역사

페라리는 1540년에 해법을 발견하였지만, 그 해법은 중간에 삼차방정식을 푸는 과정을 포함하였고, 그리하여 즉시 발표할 수 없었다. 사차방정식의 해법은 삼차방정식의 해법과 함께 페라리의 스승인 카르다노의 책에서 발표된다.

[편집]해법

$\textstyle a x^4 + b x^3 + c x^2 + d x + e = 0\$

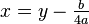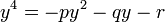이 방정식에서 양변을 $x$ 의 최고차항인 $a$ 로 나눈 다음 $\textstyle x=y- {b \over 4a}$ 라고 두면 $y^4 + p{y^2} + qy + r = 0$ 꼴로 정리할 수 있다.

$y^4 = -p{y}^2 - qy - r$ 에서 양변에 나중에 결정될 적절한 값 $z$ 를 취해서 $2zy^2 + z^2$ 을 더하면

$( y^2 + z )^2 = (2z-p){y}^2 -qy + z^2 -r$ .

이 된다. 이 우변이 완전제곱식이 되면, 사차방정식은 두 개의 이차방정식으로 분해된다. 그러므로 우변의 이차식은 판별식

$\Delta = q^2 - 4(2z-p)(z^2 -r)$

의 값이 0이 되어야 한다. 이것은 $z$ 에 대한 삼차방정식이므로 이것을 풀어 $z$ 의 값을 알아낸다. 그리하여 주어진 사차방정식은

$( y^2 + z )^2 = (sy + t)^2$

의 형태가 된다. 따라서 두 이차방정식 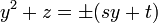$y^2 + z = \pm (sy + t)$ 을 풀어서 네 개의 해를 구한다.

[편집]특수한 경우

[편집]복이차방정식

사차 방정식 중 짝수 차수만 있는 방정식을 복이차방정식(Biquadratic equations)이라고 한다. $x^2=X$ 으로 치환해 이차방정식의 풀이를 이용해 푼다.

[편집]상반방정식

계수가 대칭적인 형태로 되어 있는 방정식을 상반방정식(Symmetric equations)이라고 한다. 사차방정식의 경우는 다음과 같다.

$a_0 x^4 + a_1 x^3 + a_2 x^2 + a_1 x + a_0 = 0$

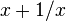이 경우 양변을 $x^2$ 으로 나누어 $x + 1/x$ 를 치환해주면 이차방정식으로 변환된다.

좀 더 일반적으로 준상반방정식(Quasi-symmetric equations)

$a_0 x^4 + a_1 x^3 + a_2 x^2 + a_1 m x + a_0 m^2 = 0$

의 경우 $x + m/x$ 으로 치환해주면 된다.

[편집]근과 계수의 관계

근과 계수의 관계 문서를 참고하십시오.

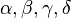사차방정식 $\textstyle ax^4 + bx^3 + cx^2 + dx + e=0$ 의 네 근을 $\textstyle \alpha, \beta, \gamma, \delta$ 라고 하면, 방정식의 계수와 근들은 다음의 관계가 성립한다.

$\textstyle \alpha + \beta + \gamma + \delta = - {b \over a}$

$\textstyle \alpha \beta + \alpha \gamma + \alpha \delta + \beta \gamma + \beta \delta + \gamma \delta = {c \over a}$

$\textstyle \alpha \beta \gamma + \alpha \beta \delta + \alpha \gamma \delta + \beta \gamma \delta = - {d \over a}$

$\textstyle \alpha \beta \gamma \delta = {e \over a}$

저작자표시 비영리 동일조건

'수학 (Mathematics) > 고,중학 수학 및 개념' 카테고리의 다른 글

번분수 (0)	2012.11.02
산술평균, 기하평균, 조화평균 사이의 부등식과 그 증명 (0)	2012.11.02
삼차 방정식 (0)	2012.11.02
이차 방정식 (0)	2012.11.02
일차 방정식 (0)	2012.11.02

3DMP