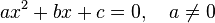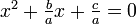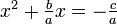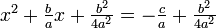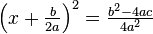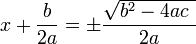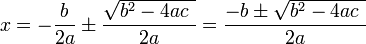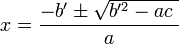이차 방정식
이차 방정식(Quadratic equation)이란, 최고차항의 차수가 2인 다항 방정식을 뜻한다.  에 관한 이차 방정식의 일반적인 모양은
에 관한 이차 방정식의 일반적인 모양은
와 같고, 여기서  는 변수,
는 변수,  와
와  는 각각
는 각각 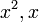 의 계수라고 하며,
의 계수라고 하며,  는 상수항이라고 부른다.
는 상수항이라고 부른다.
복소수 상에서 이차방정식은 두 복소수 해 (실근 (실수인 근)과 허근 (허수인 근으로, 보통 소문자 i로 표기한다.)이다.)를 갖는다. 이 두 해는 서로 같을 수 있고, 이 때의 근을 중근이라고 한다.
목차[숨기기] |
[편집]근의 공식
다음은 이차 방정식의 일반적인 해법인 근의 공식이다. 그 사용법은 다음과 같다.
 , 단,
, 단,  ,
,  ,
,  는 실수이고
는 실수이고  가 0이 아닐 때, 이 방정식의 두 해
가 0이 아닐 때, 이 방정식의 두 해  ,
,  는
는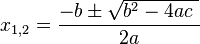 이다.
이다.
여기에서 제곱근 기호 안의 수, 즉  를 이 이차방정식의 판별식이라고 하며, 판별식의 값에 따라 방정식의 해는 세 가지로 나뉜다.
를 이 이차방정식의 판별식이라고 하며, 판별식의 값에 따라 방정식의 해는 세 가지로 나뉜다.
- 만약 판별식이 양수이면, 방정식은 서로 다른 두 실근을 갖는다.
- 만약 판별식이 0이면, 방정식은 한 개의 실근을 갖는다. 이 때의 실근을 중근이라고 한다.
- 만약 판별식이 음수이면, 방정식은 서로 다른 두 허근을 갖는다. 따라서, 실수 범위 내에서는 해가 존재하지 않는다.
[편집]근의 공식의 유도
 에서,
에서,  는
는  이 아니므로 양변을
이 아니므로 양변을  로 나눌 수 있다.
로 나눌 수 있다.
그런 다음, 상수항을 우변으로 이항하면 다음과 같은 식이 얻어진다.
좌변을 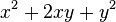 과 같은 모양으로 만들면,
과 같은 모양으로 만들면, 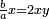 이므로
이므로  가 된다. 양변에
가 된다. 양변에  를 더해주면,
를 더해주면,
가 얻어진다. 여기에서  이므로, 좌변은
이므로, 좌변은  으로 인수분해된다. 양변을 정리하면
으로 인수분해된다. 양변을 정리하면
가 얻어지고, 제곱근을 취하면
가 얻어진다.
[편집]짝수 공식
이차 방정식에서 일차항의 계수  가 짝수인 경우
가 짝수인 경우 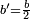 를 대입하면, 위에 제시된 근의 공식을 이용하는 것보다 아래의 짝수 공식을 이용하는 쪽이 더 간단하게 표현된다.
를 대입하면, 위에 제시된 근의 공식을 이용하는 것보다 아래의 짝수 공식을 이용하는 쪽이 더 간단하게 표현된다.
[편집]근과 계수의 관계
 근과 계수의 관계 문서를 참고하십시오.
근과 계수의 관계 문서를 참고하십시오.
[편집]근의 공식을 이용한 근과 계수의 관계 증명
 의 두 근
의 두 근 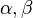 는 각각
는 각각
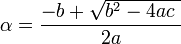
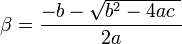 이라고 하면(순서는 바뀌어도 무관)
이라고 하면(순서는 바뀌어도 무관)
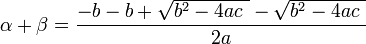

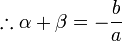

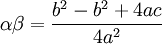
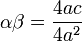

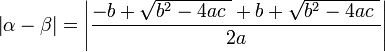
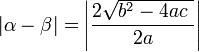

[편집]이차방정식 만들기를 이용한 근과 계수의 관계 증명
 의 두 근을 각각
의 두 근을 각각 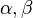 라고 정의하고
라고 정의하고
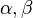 을 근으로 갖는 이차방정식을
을 근으로 갖는 이차방정식을  이라 한 후
이라 한 후
이 이차방정식 앞에 계수  를 붙여주면(∵ 계수를 붙이건 안 붙이건 근은 같으므로)
를 붙여주면(∵ 계수를 붙이건 안 붙이건 근은 같으므로)
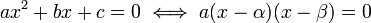
(∵ 두 이차방정식의 해가 같으므로)
먼저 두 번째 이차방정식인  의 계수를 나누고 전개해주면
의 계수를 나누고 전개해주면
 - ⓐ
- ⓐ
또한, 첫 번째 이차방정식인  또한 두 번째 이차방정식을 전개할 때와 마찬가지로
또한 두 번째 이차방정식을 전개할 때와 마찬가지로
최고차항 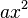 의 계수
의 계수  로 나눠주면
로 나눠주면
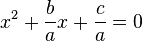 - ⓑ
- ⓑ
ⓐ = ⓑ 이므로, 따라서


'수학 (Mathematics) > 고,중학 수학 및 개념' 카테고리의 다른 글
| 사차 방정식 (0) | 2012.11.02 |
|---|---|
| 삼차 방정식 (0) | 2012.11.02 |
| 일차 방정식 (0) | 2012.11.02 |
| 유한확정 (0) | 2012.11.02 |
| 지수법칙 자연수,정수,유리수,실수 [영상강의 링크] (0) | 2012.11.02 |


 의 그래프.
의 그래프.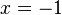 과
과  는
는 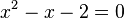 이라는 이차방정식의 해가 된다.
이라는 이차방정식의 해가 된다.