기저(basis)와 좌표계(coordinate system), 고유값(eigenvalue)과 고유벡터(eigenvector)
>> 기저(basis)와 좌표계(coordinate system)
선형대수에서 기저(basis)라 함은 임의의 벡터공간 V에 대해서 어떤 벡터집합 S가 서로 “1차독립”이면서 벡터공간 V를 “생성”하면 벡터집합 S를 벡터공간 V의 기저라고 합니다.
사실 위의 기저에 대한 정의는 지극히 수학교과서적인 정의이죠. 기저에 대한 모든 의미가 다 담겨있기는 하지만 이런 딱딱한 정의 내용을 보고 해당 정의가 의미하는 모든 것을 집어내기에는 어지간한 수학적 감각이 있지 않다면 어려울 것으로 생각됩니다. 물론 질문자 분께서도 같은 이유로 인해서 좀 더 쉽게 이해할 수 있는 방법에 대해 질문을 했을 것으로 생각됩니다.
이런 엄밀하고 딱딱한 정의에서 벗어나 기존에 우리가 주로 활용하면서 익숙해져 있는 직각좌표계를 가지고 선형대수에서의 기저에 대한 이해를 할 수 있도록 설명을 한번 해 보고자 합니다. 물론 이런 느슨하고 부드러운 설명들은 수학적인 허점을 드러낼 수 있으므로 대충의 감과 이해를 얻고자 하는데 그 목적이 있으며, 이 이해를 바탕으로 다시 한번 엄밀한 정의를 검토함으로써, 해당 정의가 의미하는 바를 좀 더 깊이 있게 이해할 수 있도록 하면 되겠습니다.
우선 우리에게 익숙한 2D 직교좌표계를 떠올려 보죠. 두 좌표축을 각각 x, y라고 하고 이 x, y 좌표 평면위의 모든 점에 대해서 x, y에 대한 좌표값 (a, b)로 표현할 수 있다는 것을 배워왔습니다. 여기서 x, y 좌표 평면위의 모든 점을 나타내어 주는 좌표값들은 수의 순서 짝으로써 벡터로 해석될 수 있습니다. 그리고 이 각각의 좌표축을 나타내는 두 단위벡터를 다음과 같이 생각할 수 있겠죠.
v1 = (1, 0)
v2 = (0, 1)
여기서는 좌표축을 나타내는 기준벡터로써 길이가 1인 단위벡터를 사용했지만 벡터의 길이는 크게 중요하지 않습니다. 다만 길이가 0이 아닌 벡터이면 충분하다는 사실을 1차독립, 1차결합 등이 무엇을 의미하는지 아신다면 이해하실 겁니다. (1차독립과 1차결합은 기저를 이해하는데 중요한 개념이므로 이에 대한 이해가 없으시다면 먼저 교재를 통해서 이에 대한 이해를 구하시는 것이 좋겠습니다.)
위의 두 벡터 v1, v2는 서로 1차독립이면서 동시에 1차결합을 통해서 2D 직교좌표계의 모든 점을 표현할 수 있는 벡터공간을 생성함을 알 수 있습니다. 따라서 위의 두 벡터의 집합 S = {v1, v2}는 2D 직교좌표계의 벡터공간 V를 생성하는 기저라고 할 수 있습니다.
마찬가지로 3D 직교좌표계에 대해서 각각의 좌표축에 대한 단위벡터는 아래와 같습니다.
v1 = (1, 0, 0)
v2 = (0, 1, 0)
v3 = (0, 0, 1)
그리고 이 벡터들의 집합 S = {v1, v2, v3}는 3D 직교좌표계의 벡터 공간을 생성하는 기저라고 할 수 있습니다. 이해를 돕기 위해서 실제 예를 하나 들자면, 3D 직교좌표계 내의 한 점(벡터) (2, 5, 7)을 기저들의 일차결합으로 나타내면 아래와 같이 되겠죠.
2 (1, 0, 0) + 5 (0, 1, 0) + 7 (0, 0, 1) = (2, 5, 7)
그리고 3D 직교좌표계 내의 모든 점들은 위와 같이 기저 S를 사용한 1차결합으로 표현할 수 있으며, 따라서 집합 S는 3D 직교좌표계의 벡터 공간을 생성하는 기저라 할 수 있습니다.
이제 기저와 좌표계에 대해서 조금 이해가 되셨는지 모르겠네요. 선형대수를 공부하기 전까지 우리는 막연히 좌표계를 세우고 해당 좌표계 내에서의 모든 점들을 수의 순서 짝으로 표현 하는 방법에 대해서 배웁니다. 그리고 이 개념들이 선형대수를 배우면서 좌표계는 각 좌표축을 대표하는 벡터들을 기저로 하는 벡터공간이며, 이 공간내의 모든 점들은 수의 순서 짝으로써 벡터로 해석될 수 있으며, 해당 벡터들은 기저 벡터들의 일차결합으로 표현할 수 있다는 사실을 이해하게 됩니다.
그리고 이러한 사실들을 일반화함으로써, 기하학적으로 구상화할 수 없는 4차원 이상의 고차원에 대한 벡터에 대해서도 똑같이 적용할 수 있는 여러 벡터 연산들의 성질들을 연구할 수 있게 됩니다. 그리고 이런 수학적인 정리와 증명들은 각종 이공계의 여러 분야에서 상상 이상의 응용력을 발휘하며 인류 사회의 발전에 막대한 공헌을 한다고 할 수 있겠습니다.
사실 위에서는 직관적인 이해를 돕기 위해서 2D, 3D의 직교좌표계라는 벡터공간의 특수한 경우로만 설명을 했지만, 선형대수를 조금 더 공부하시다 보면 일반화에 의한 차원의 확장이라든지, 또는 직교좌표계는 직교기저들이 이루는 벡터공간으로써 일반적인 벡터공간의 특수한 한 경우에 불과하다는 점 등을 이해하게 되실 겁니다. 다만, 여러 응용분야에 있어서 정규직교기저에 의한 벡터공간은 특히 유용하게 사용되는 경우가 많으므로, 정규직교기저에 대한 성질이 더 중요하게 다루어지기도 합니다.
간단하게 실례를 든다면, 물리학에서 운동의 법칙을 배울 때, 처음에는 일차원 운동으로 개념을 잡습니다. 하지만 2, 3차원 혹은 그 이상의 차원으로 이 운동의 법칙을 확장하는 것은 의외로 쉽습니다. 그것을 가능하게 해주는 것이 바로 벡터공간에 대한 수학적 연구의 결과입니다. 그리고 혹시 컴퓨터 3D 게임을 하시는지는 모르겠지만, 선형대수에서의 3차원 정규직교기저에 대한 연구 결과의 응용 없이는 컴퓨터의 3D 그래픽스라는 분야 자체가 존재할 수 없습니다. 이것은 제가 3D 프로그래머로써 현업에서 응용을 하고 있기에 장담할 수 있습니다. 선형대수가 없는 3D 그래픽 소프트웨어 개발은 상상조차 할 수 없습니다.
설명이 많이 부족하기는 하지만 위에서 언급한 2/3 차원 직교좌표계가 어떻게 벡터공간으로 대응이 되는지에 대한 이해를 바탕으로 다시 한번 교재의 정의를 살펴봄으로써 기저에 대한 이해 및 기저와 좌표계 사이의 관계에 대한 이해를 구하시면 도움이 되실 것이라 생각합니다.
>> 고유값(eigenvalue)과 고유벡터(eigenvector)
고유값과 고유벡터에 대한 정의는 그리 어려운 것이 아닙니다만, 기저를 설명할 때 언급했던 것처럼 정의만 보고 고유값과 고유벡터가 도대체 뭔지 이해를 하는 것이 쉽지만은 않죠. 하지만 선형대수에 있어서 고유값과 고유벡터에 대한 이해는 상당히 중요합니다. 아마 질문자 분께서 이 고유값과 고유벡터에 대한 내용을 제대로 이해하신다면, 벡터에 선형변환을 가하는 선형 연산자로써의 행렬이라는 존재에 대해서 조금 더 깊이 이해할 수 있는 계기가 될 수 있을 것입니다.
다만, 걱정되는 것은 저의 짧은 지식에 의한 설명으로 제대로 의미 전달이 가능할 것인가가 문제라면 문제겠죠. 어쨌든 시작해 보도록 하겠습니다. 고유값, 고유벡터에 대한 교과서적인 정의는 다음과 같습니다.
A가 행렬이고 같은 차원의 벡터 x에 대해서 Ax = λx를 만족하면, 스칼라 λ를 행렬 A의 고유값이라 하고, 벡터 x를 스칼라 λ에 대응하는 행렬 A의 고유벡터라고 한다.
고유값과 고유벡터에 대한 정확한 이해를 위해서 먼저 고유값과 고유벡터의 기하학적인 성질을 설명을 드리자면, 행렬 A가 어떤 벡터 x에 선형변환을 가하는 선형연산자일 때, 즉 회전변환과 확대/축소 변환을 가하는 연산자일 때, 해당 벡터 x에 대해서 회전변환은 가하지 않고 확대/축소 변환만을 가한다면 이 벡터 x는 A의 고유벡터가 된다는 뜻입니다. 그리고 이런 경우 확대/축소의 양을 나타내는 스칼라를 따로 분리할 수 있게 되는데 이 스칼라 값이 고유값 λ가 된다는 의미입니다.
이해를 돕기 위해서 실제 계산을 한번 해 보겠습니다. 예를 들어서 확대연산자의 표준 행렬이라고 할 수 있는 다음 행렬에 아무 벡터나 곱해보면 위에서 보았던 Ax = λx를 만족한다는 것을 쉽게 알 수 있습니다.
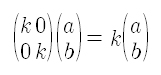
위의 행렬에서는 결국 (1, 0)과 (0, 1) 두 개의 고유벡터가 존재하며 이들 각각에 대응되는 고유값은 k가 된다는 것을 알 수 있습니다. 여기서 자세한 계산 과정을 적지는 않겠습니다. 계산은 책을 보고 훈련을 통해서 익히면 그만입니다. 이해가 없는 계산은 아무짝에 쓸모없는 소모전에 불과 하므로 여기서는 이해에 중점을 맞출 것이며 될 수 있으면 구체적인 계산은 피하도록 하겠습니다. 위의 행렬로 직접 한번 고유값과 고유벡터를 계산해 보시고 결과를 확인해 보세요.
자, 이쯤 왔으면 뭔가 딱 느껴지는 것이 있어야 합니다. 위의 행렬은 어떤 벡터이든지 Ax = λx를 만족하는 변환을 가합니다. 그리고 이러한 벡터들은 고유벡터인 (1, 0), (0, 1) 두 벡터의 선형결합에 의해 표현될 수 있습니다. 그리고 이 두 고유벡터는 일반적으로 생각하는 2차원의 정규직교기저벡터와 정확하게 일치합니다.
우리는 고유값과 고유벡터의 기하학적 성질을 알 고 있으므로, 위 형태의 행렬이 2차원 정규직교기저가 생성하는 벡터 공간에서 확대/축소 연산을 가하는 표준 행렬이라는 것을 쉽게 알 수 있습니다. 그리고 이쯤에서 어떤 행렬 A가 있을 때, 그 행렬로부터 힘들게 계산해서 구해내는 고유값과 고유벡터가 어떤 의미인지를 어느 정도는 이해할 수 있을 것이라 생각합니다.
설명을 계속해 보겠습니다. 여기서 부터는 잘 따라오셔야 합니다. 일반적으로 우리가 머릿속에 그리는 2차원 직교좌표계에서의 벡터들에게 선형연산을 가하는 어떤 행렬 A가 있을 때, 이 행렬 A가 위에서 본 확대/축소 행렬의 형태가 아닌 이상, 그 행렬이 2차원 정규직교기저가 만드는 벡터공간 내에서는 확대/축소 뿐 아니라 회전변환까지도 가하게 됩니다. 즉, 이것은 이 행렬 A가 2차원 정규직교기저의 벡터 공간에서는 벡터들에게 어떤 변환을 가할지 계산하기가 복잡하다는 의미가 됩니다. 단순히 확대/축소 변환만 가하는 행렬과 확대/축소 및 회전변환까지 가하는 행렬 중 어느 행렬이 더 이해하기 쉽고 계산하기 쉬우며 더 나아가 어떤 문제 해결에 응용하기 쉬운지는 이견의 여지가 없을 것입니다.
이제 어느 정도 결론에 도달해 가는 것 같습니다. 이제 우리는 어떤 선형연산자로써의 행렬이 있을 때, 이 행렬로부터 고유값과 고유벡터를 계산해 냄으로써, 이 행렬이 벡터에 가하는 변환을 고유벡터들이 기저를 이루는 고유공간에서의 변환으로 해석함으로써, 회전 변환은 배제하고 확대/축소 변환만으로 이해하고 응용할 수 있게 되었습니다.
확실한 이해를 위해서 구체적인 예를 한 가지만 들어 보겠습니다. 다음과 같은 행렬 A가 있습니다.
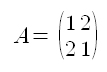
위 행렬 A의 고유벡터는 v1 = (1, 1), v2 = (-1, 1) 이고, 고유값은 λ1 = 3, λ2 = -1입니다. 그러면 이 행렬 A가 벡터 x = (x1, x2) 에 변환을 가할 때, 이 변환을 고유벡터 v1, v2가 기저를 이루어 생성하는 고유벡터 공간에서 이해를 하면, v1 방향으로는 3배, v2 방향으로는 -1배한 벡터들의 합으로 변환이 가해진다는 것을 알 수 있습니다.
위 설명이 사실인지 직접 계산을 통해서 이해를 해 보죠.
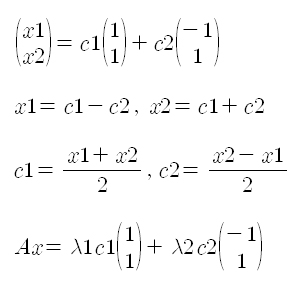
위의 풀이 과정으로 x = (2, 3) 인 경우를 계산해 보면 Ax = (8, 7) 이 나온다는 것을 알 수 있습니다. 그리고 이것은 실제 Ax를 행렬 계산으로 계산했을 때 구해지는 값이기도 하다는 것을 확인해 보시기 바랍니다. 그리고 이것을 그림으로 나타내면 아래 그림과 같습니다.
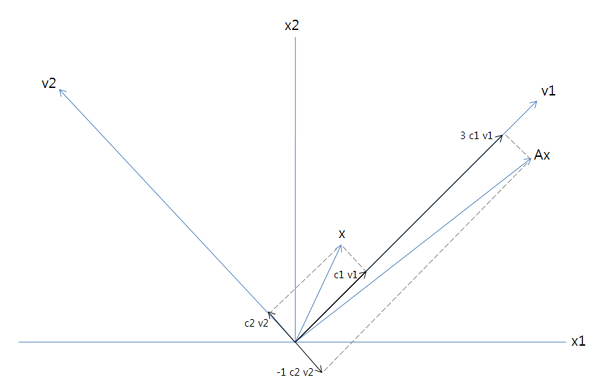
위 그림을 보시면 보다 더 명확하게 이해가 가실 겁니다. 즉, 행렬 A가 벡터 x에 가하는 변환을 행렬 A의 고유벡터들이 기저를 이루어서 생성되는 고유공간에서 이해를 하면, 고유 벡터들의 확대/축소 연산만을 가지고도 이 변환을 이해할 수 있게 된다는 것입니다. 이것이 원래의 직교기저가 생성하는 벡터 공간에서의 변환을 이해하는 것 보다 훨씬 쉽다는 것을 그림을 통해서 이해해 보시기 바랍니다. 그리고 이러한 결과로 인해서 고유값과 고유벡터의 개념은 이공계 분야에서 상당히 중요한 응용에 사용되는 경우가 아주 아주 많습니다.
자, 이제 어느 정도 이해가 되셨으리라 생각합니다. 항상 느끼는 거지만, 수학이란 학문은 수식을 제외하고 말로만 설명을 하려면 상당히 힘들죠. 하지만 바꾸어 말하면 수식으로만 설명이 된 내용들은 탁월한 감각이 있지 않은 사람들이 보기에는 쉽게 이해하기가 힘들다는 것도 분명한 사실입니다. 저 역시도 후자에 속하는 한 사람으로써 고유값과 고유벡터를 이해하는데 애를 먹었던 기억이 있습니다.
짧은 지식으로, 그리고 말로 수학을 설명 하느라 핵심 내용이 어느 정도로 잘 전달되었는지 모르겠지만, 그래도 어렴풋이나마 이해를 하셨다면 여기서의 이해를 잘 떠올리면서 다시 한번 교재의 정의들과 응용에 활용되는 예제들을 풀어 보시기 바랍니다. 분명 이전에 잘 모르고 공식으로만 풀어내던 고유값과 고유벡터에 대해 새로운 눈을 뜨게 되실 것이라 생각합니다. 아울러 아까도 잠깐 업급 했지만, 선형연산자로써의 행렬을 바라보는 눈도 이전 보다는 한층 더 발전된 시각으로 바로 볼 수 있게 되었기를 바래봅니다.
그럼 행운을 빕니다.
참고]
'수학 (Mathematics) > 3D수학' 카테고리의 다른 글
| 동차 좌표 (0) | 2012.11.02 |
|---|---|
| 아핀공간과 볼록집합 (0) | 2012.11.02 |
| IntersectTriangle 분석 (0) | 2012.11.02 |
| 픽킹 ( 광선과 오브젝트 충돌판정 ) (0) | 2012.11.02 |
| 3D 기하학 (0) | 2012.11.02 |
