copyrightⓒ 김성수 [2002년 05월 26일]
이글은 D3D의 Pick예제에 나와있는 IntersectTriangle에 관한 설명입니다. 이 함수가 하는일이나 사용법에 대해선 예제에 잘 나와있기때문에 이런것을 설명하지는 않습니다. 이글의 목적은 함수 자체가 어떤 원리로 동작을 하는지를 이해하는것이죠.
IntersectTriangle은 단순히 소스분석만해서는 도저히 이해를 할 수 없습니다.
가뜩이나 벡터연산이 복잡해 머리가 아픈데, 수학적인 레벨에서 최적화를 해놓았으니 더욱 암호처럼 보일수 밖에....
그럼 IntersectTriangle의 동작원리에 대해 하나씩 알아보겠습니다.
1. 삼각형 점포함 테스트
IntersectTriangle이 반직선과 삼각형의 교차판정을 하는방법은 2차원적으로 해석될수 있습니다.
반직선과 삼각형 평면의 교점이 삼각형에 포함되는지를 검사하는것이죠.
그런데 특별한 사정때문에 이전에 제가 썼던 글에 있는 점포함테스트를 사용하지 않습니다.
약간은 특이한 방법을 쓰게되죠.
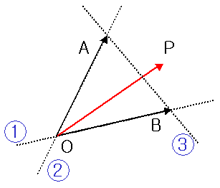
그림을 보시면 벡터가 세개 나옵니다. OA,OB는 고정된 벡터이고 OP는 임의의 벡터입니다.
임의의 벡터 OP를 벡터 OA,OB를 가지고 표현해 봅시다.
OP = u * OA + v * OB ( u,v는 임의의 실수 ) 벡터의 영역문제에서 자주본 꼴이죠? (생각이안나는 사람은..정석을 뒤져봅시다)
u와 v에 제약을 가하면 점P는 특정한 영역을 표현하게 됩니다.
옴옴...뭘하려는지 알겠다고요?
그렇습니다. u,v에 어떤 조건을 붙여서 P가 삼각형 OAB영역을 표현하도록 하려는겁니다.
P가 OAB영역을 표현하기위한 조건은, 삼각형의 변(①②③)에대해 각각 하나씩 있습니다.
① : 0 ≤ u
② : 0 ≤ v
③ : u + v ≤ 1
이 조건들은 알아서덜 증명을... (①②번 조건은 말이 필요없고...③번조건은 직선 AB가 t*OA + (1-t)*OB 임을 이용)
위조건을 만족하는 u,v에 대해 P가 표현하는 영역은 삼각형 OAB입니다.
점 P가 삼각형 OAB에 포함되는지를 검사하는것은 u,v가 위조건을 만족하는지를 검사하는것과 같다는 얘기.
IntersectTriangle이 출력하는 u,v가 지금껏 이야기해온 u,v입니다. 반직선과 삼각형 평면의 교점이 P, 삼각형의 각 꼭지점이 O,A,B인 셈이죠. 따라서 반직선과 삼각형의 교차판정은 코드중에 다음처럼 나타납니다.
마우스의 3차원좌표 = v0 + u * ( v1 - v0 ) + v * ( v2 - v0 )
카메라와의 거리 = |마우스의 3차원좌표-orig|
2. 벡터분해
문제는 OP를 OA,OB로 표현하는것. 다시말해 u,v값을 어떻게 구하는가 하는것입니다.
이제 OP를 OA,OB로 분해하는법을 생각해봅시다.
임의의 벡터 OP를 벡터 OA,OB를 가지고 표현해 봅시다.
u와 v에 제약을 가하면 점P는 특정한 영역을 표현하게 됩니다.
옴옴...뭘하려는지 알겠다고요?
그렇습니다. u,v에 어떤 조건을 붙여서 P가 삼각형 OAB영역을 표현하도록 하려는겁니다.
P가 OAB영역을 표현하기위한 조건은, 삼각형의 변(①②③)에대해 각각 하나씩 있습니다.
① : 0 ≤ u
② : 0 ≤ v
③ : u + v ≤ 1
이 조건들은 알아서덜 증명을... (①②번 조건은 말이 필요없고...③번조건은 직선 AB가 t*OA + (1-t)*OB 임을 이용)
위조건을 만족하는 u,v에 대해 P가 표현하는 영역은 삼각형 OAB입니다.
점 P가 삼각형 OAB에 포함되는지를 검사하는것은 u,v가 위조건을 만족하는지를 검사하는것과 같다는 얘기.
IntersectTriangle이 출력하는 u,v가 지금껏 이야기해온 u,v입니다. 반직선과 삼각형 평면의 교점이 P, 삼각형의 각 꼭지점이 O,A,B인 셈이죠. 따라서 반직선과 삼각형의 교차판정은 코드중에 다음처럼 나타납니다.
if( *u < 0.0f || *u > det )
return FALSE;
if( *v < 0.0f || *u + *v > det )
return FALSE;
Picking일 경우 IntersectTriangle이 출력하는 u,v를 사용하면 마우스의 3차원 위치와 카메라와의 거리를 쉽게 구할수 있습니다.카메라와의 거리 = |마우스의 3차원좌표-orig|
2. 벡터분해
문제는 OP를 OA,OB로 표현하는것. 다시말해 u,v값을 어떻게 구하는가 하는것입니다.
이제 OP를 OA,OB로 분해하는법을 생각해봅시다.
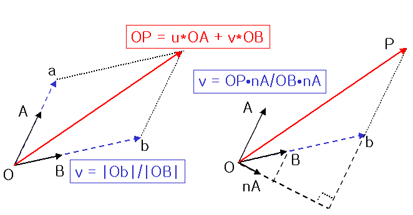
왼쪽그림을 보면 v = |Ob| / |OB| 임을 쉽게 알 수 있죠?
이때 벡터 OB와 Ob를 OA에 수직인 벡터 nA에 투영을 한것이 오른쪽 그림입니다.
보다시피 한쌍의 닮은꼴 삼각형이...... 옴옴...그냥 아래식을 주욱 읽으시면 걍 이해가....
(도데체 그림때문에 설명할게 없잖아!...ㅡ.ㅡ;;)v = |Ob|/|OB| = |Ob||nA|cosθ/|OB||nA|cosθ = Ob•nA/OB•nA 여기서 벡터 Ob와 OP는 법선 nA에 대해 같은 정사영을 갖습니다.Ob•nA = OP•nA
∴v = Ob•nA/OB•nA = OP•nA/OB•nA 같은 방법으로 u를 표현하면..u = OP•nB/OA•nB 이제 법선과 내적값을 구하는일만 남았군요.
3. 내적값(OP•N)과 법선(N)
실제로 IntersectTriangle은 공간상의 반직선과 평면의 교점(P)을 구하지 않고 u,v값을 계산해 냅니다.
교점이 없이도 OP•N 값을 알아내는 방법이 있기때문인데요, 바라보는 방향에 비책이 숨어 있습니다
이때 벡터 OB와 Ob를 OA에 수직인 벡터 nA에 투영을 한것이 오른쪽 그림입니다.
보다시피 한쌍의 닮은꼴 삼각형이...... 옴옴...그냥 아래식을 주욱 읽으시면 걍 이해가....
(도데체 그림때문에 설명할게 없잖아!...ㅡ.ㅡ;;)
∴v = Ob•nA/OB•nA = OP•nA/OB•nA
3. 내적값(OP•N)과 법선(N)
실제로 IntersectTriangle은 공간상의 반직선과 평면의 교점(P)을 구하지 않고 u,v값을 계산해 냅니다.
교점이 없이도 OP•N 값을 알아내는 방법이 있기때문인데요, 바라보는 방향에 비책이 숨어 있습니다
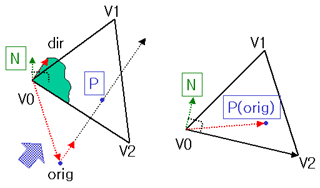
왼쪽그림은 IntersectTriangle의 입력들을 그려놓은것입니다. 오른쪽 그림은 이것을 dir과 평행한 방향으로 바라본 그림이고요.
그림에 표시된 법선(N)은 V0,V2를 포함하고 바라보는 방향과 평행한 평면의 법선벡터입니다.
이때, 점 P와 orig는 이 벡터(N)에대해 '같은 정사영'을 갖는 점들임을 알수 있습니다. 즉 다음이 성립한다는 말이죠.
(orig-V0)•N == (P-V0)•N N을 법선으로 하는 평면은 V0,V2,(V0+dir)을 포함하는 평면이고(dir과 평행한 방향으로 바라봤으므로),
따라서 법선 N은 다음과같이 구해집니다.N = dir ⅹ ( V2 - V0 )
연산자 'ⅹ' 가 외적인건 아시죠?
이제 모든값을 알았으니 정리를 좀 해볼까요?
u = tvec • ( dir ⅹ e2 ) / e1 • ( dir ⅹ e2 ) 음...갑자기 이상한것들이 튀어나와서 죄송. 식을 쓰다보니 점점 길어지는것 같아서...
앞으로는 아래와 같은 정의를 사용하도록 하겠습니다.e1 = V1 - V0
e2 = V2 - V0
tvec = orig - V0 이제야 소스의 다음부분에 대한 설명이 끝났군요.
나머지는 최적회일 뿐이죠.
4. 최적화
u를 구한것과 같은 방법으로 v를 구해 봅시다.v = tvec • ( e1 ⅹ dir ) / e2 • ( e1 ⅹ dir ) 여기에 약간의 수학적성질을 적용해보면 재미있는 사실을 알게됩니다.A•(BⅹC) = B•(CⅹA) = C•(AⅹB)
이것을 이용해서 v의 분모부분을 변형해볼까요?e2 • ( e1 ⅹ dir ) = e1 • ( dir ⅹ e2 ) 오호...잘보니 v,u의 분모부분이 같은넘이었군요!
분자부분도 같은방법으로 변형시켜보면 소스코드가 이해가 되실겁니다.
(이것두 역시 최적화. 나중에 t 를 계산할때 외적결과를 또 써먹으려고 변형을 해 놓은거죠. )
이것으로 다음소스에 대한 설명이 끝났습니다.
그중 하나가 첫번째 나온 비교문입니다.
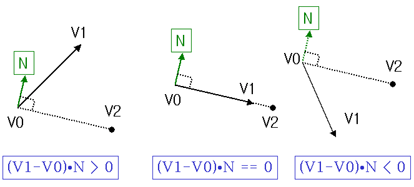
이 조건이 참이되는 경우를 생각해 보도록 합시다. det값은 법선벡터 N과 변벡터 e1의 내적값입니다.
이값이 0이면 삼각형은 dir과 평행한 평면에 존재하는것 입니다. 만약 이 값이 0보다 작으면 삼각형이 뒤집어져 있는경우죠.
그림에 표시된 법선(N)은 V0,V2를 포함하고 바라보는 방향과 평행한 평면의 법선벡터입니다.
이때, 점 P와 orig는 이 벡터(N)에대해 '같은 정사영'을 갖는 점들임을 알수 있습니다. 즉 다음이 성립한다는 말이죠.
따라서 법선 N은 다음과같이 구해집니다.
이제 모든값을 알았으니 정리를 좀 해볼까요?
앞으로는 아래와 같은 정의를 사용하도록 하겠습니다.
e2 = V2 - V0
tvec = orig - V0
D3DXVec3Cross( &pvec, &dir, &edge2 ); FLOAT det = D3DXVec3Dot( &edge1, &pvec ); *u = D3DXVec3Dot( &tvec, &pvec ); FLOAT fInvDet = 1.0f / det; *u *= fInvDet;사실 여기까지가 설명의 끝입니다.
나머지는 최적회일 뿐이죠.
4. 최적화
u를 구한것과 같은 방법으로 v를 구해 봅시다.
분자부분도 같은방법으로 변형시켜보면 소스코드가 이해가 되실겁니다.
(이것두 역시 최적화. 나중에 t 를 계산할때 외적결과를 또 써먹으려고 변형을 해 놓은거죠. )
이것으로 다음소스에 대한 설명이 끝났습니다.
D3DXVec3Cross( &qvec, &tvec, &edge1 ); *v = D3DXVec3Dot( &dir, &qvec ); *v *= fInvDet;IntersectTriangle은 연산을 수행하는 도중 판정결과를 알 수 있다면 바로 리턴하는 방식으로, 필요없는 연산이 일어나지 않도록 구성되어있습니다.
그중 하나가 첫번째 나온 비교문입니다.
if( det < 0.0001f )
return FALSE;
이 비교문은 코딩 차원에서 본다면 0으로 나누는 에러방지와 det값과 u,v값의 비교를 쉽게해주는 역할을 합니다만, 수학적으로 보면 이코드의 또다른면을 볼 수 있게됩니다.이 조건이 참이되는 경우를 생각해 보도록 합시다. det값은 법선벡터 N과 변벡터 e1의 내적값입니다.
이값이 0이면 삼각형은 dir과 평행한 평면에 존재하는것 입니다. 만약 이 값이 0보다 작으면 삼각형이 뒤집어져 있는경우죠.
| 여기서 잠깐! D3D8.1 버젼부터는 det에 절대값을 취함으로써 뒤집어진 면도 교차라고 판정하도록 되어있습니다. 사실 이전 버젼의 예제들은 det값을 그대로 사용해서, IntersectTriangle함수가 반직선과 삼각형의 교차판정뿐 아니라 뒤집어진 삼각형이 아닌지까지 검사하도록 만들어져 있었던겁니다. 이것을 함수의 목적에 맞도록 수정했다고나 할까요? 하지만 det에 절대값을 취하는 부분만 없애면 '별도의 연산없이' 뒤집어진 삼각형을 검사해낼 수 있다는것을 꼭 알아두시길... |
5. t : orig와 P 의 거리
소스에대한 의문들이 풀리셨나 모르겠습니다. 근데 교차판정과는 전혀 상관없는 코드가 하나 더있네염. 안그래두 엄청시리 길어졌는데...그렇다고 안하고 놔두자니 영 찜찜...
다음은 아직 설명하지 않은 '유일한' 코드입니다.
*t = D3DXVec3Dot( &edge2, &qvec );
*t *= fInvDet;
우선 설명을 하기전에 t와 det를 적당히 변형하도록 하겠습니다.( 각종 연산결과들을 최대한 재사용하려고 변형해 놓은거라서 변형하지 않고는 설명이 넘 어렵습니다. )
t = e2 • ( tvec ⅹ e1 ) = tvec • ( e1 ⅹ e2 ) = -tvec • ( e2 ⅹ e1 )
( ∵ AⅹB = -BⅹA )
(삼각형을 옆에서 바라봤으니 삼각형은 선분으로 보입니다.)
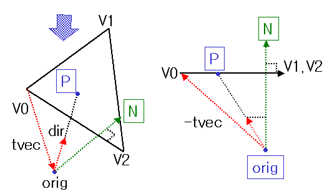
우리가 구하고자 하는 t는 dir을 단위로하는 시점에서 교점까지의 거리입니다.|P-orig| = t * |dir|
∴ t = |P-orig|/|dir| = |P-orig||N|cosθ/|dir||N|cosθ = (P-orig)•N / dir•N
(여기서 N = e2 ⅹ e1 ) 근데 N에 대해서 벡터 P-orig 와 -tvec이 같은 정사영을 갖습니다. 따라서...(P-orig)•N == (-tvec)•N
∴ t = (P-orig)•N / dir•N = (-tvec)•N / dir•N
우~~~아~~~~~정말로 길군요.
말로 설명하면 금방될것을....황금같은 주말에 이틀동안 집에 틀어밖혀서 이것만 써댔네염.....T.T...
이것으로 소스가 완전히 이해되셨기를 바랍니다.
이해가 안되신다면 질문주세염.
거럼...오늘 프랑스전.... 2:1 에 5000원 걸었는데......
'한국승'에 걸었답니다. 코리아팀 파이팅! o(^O^)O
- 참고소스 DX8 -
∴ t = |P-orig|/|dir| = |P-orig||N|cosθ/|dir||N|cosθ = (P-orig)•N / dir•N
(여기서 N = e2 ⅹ e1 )
∴ t = (P-orig)•N / dir•N = (-tvec)•N / dir•N
우~~~아~~~~~정말로 길군요.
말로 설명하면 금방될것을....황금같은 주말에 이틀동안 집에 틀어밖혀서 이것만 써댔네염.....T.T...
이것으로 소스가 완전히 이해되셨기를 바랍니다.
이해가 안되신다면 질문주세염.
거럼...오늘 프랑스전.... 2:1 에 5000원 걸었는데......
'한국승'에 걸었답니다. 코리아팀 파이팅! o(^O^)O
- 참고소스 DX8 -
//-----------------------------------------------------------------------------
// Name: IntersectTriangle()
// Desc: Given a ray origin (orig) and direction (dir), and three vertices of
// of a triangle, this function returns TRUE and the interpolated texture
// coordinates if the ray intersects the triangle
//-----------------------------------------------------------------------------
BOOL CMyD3DApplication::IntersectTriangle( const D3DXVECTOR3& orig,
const D3DXVECTOR3& dir, D3DXVECTOR3& v0,
D3DXVECTOR3& v1, D3DXVECTOR3& v2,
FLOAT* t, FLOAT* u, FLOAT* v )
{
// Find vectors for two edges sharing vert0
D3DXVECTOR3 edge1 = v1 - v0;
D3DXVECTOR3 edge2 = v2 - v0;
// Begin calculating determinant - also used to calculate U parameter
D3DXVECTOR3 pvec;
D3DXVec3Cross( &pvec, &dir, &edge2 );
// If determinant is near zero, ray lies in plane of triangle
FLOAT det = D3DXVec3Dot( &edge1, &pvec );
D3DXVECTOR3 tvec;
if( det > 0 )
{
tvec = orig - v0;
}
else
{
tvec = v0 - orig;
det = -det;
}
if( det < 0.0001f )
return FALSE;
// Calculate U parameter and test bounds
*u = D3DXVec3Dot( &tvec, &pvec );
if( *u < 0.0f || *u > det )
return FALSE;
// Prepare to test V parameter
D3DXVECTOR3 qvec;
D3DXVec3Cross( &qvec, &tvec, &edge1 );
// Calculate V parameter and test bounds
*v = D3DXVec3Dot( &dir, &qvec );
if( *v < 0.0f || *u + *v > det )
return FALSE;
// Calculate t, scale parameters, ray intersects triangle
*t = D3DXVec3Dot( &edge2, &qvec );
FLOAT fInvDet = 1.0f / det;
*t *= fInvDet;
*u *= fInvDet;
*v *= fInvDet;
return TRUE;
}반응형
'수학 (Mathematics) > 3D수학' 카테고리의 다른 글
| 아핀공간과 볼록집합 (0) | 2012.11.02 |
|---|---|
| 기저(basis)와 좌표계(coordinate system), 고유값(eigenvalue)과 고유벡터(eigenvector) (0) | 2012.11.02 |
| 픽킹 ( 광선과 오브젝트 충돌판정 ) (0) | 2012.11.02 |
| 3D 기하학 (0) | 2012.11.02 |
| 반사벡터와 미끄러짐 벡터 (0) | 2012.11.02 |

