http://yeols.com/80074139499
![]() 힙 정렬(Heap Sort)
힙 정렬(Heap Sort)![]()
- 고급 정렬 알고리즘(병합 정렬, 퀵 정렬, 힙 정렬) 중 하나.
먼저, 힙 정렬을 알아보기 전에 힙 정렬에 필요한 이진 트리(Binary Tree)의 개념 부터 알고 넘어가자. - 이진 트리(Binary Tree)
- 최대 두 개까지의 자식 노드를 가질 수 있는 트리
- 하나의 노드는 0, 1 혹은 2개의 서브 트리를 가질 수 있다.
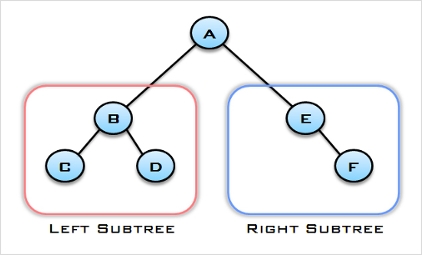
- 좌 서브 트리(Left Subtree)
- 우 서브 트리(Right Subtree)
- 널 트리(Null tree)
- 어떠한 노드도 가지고 있지 않은 트리
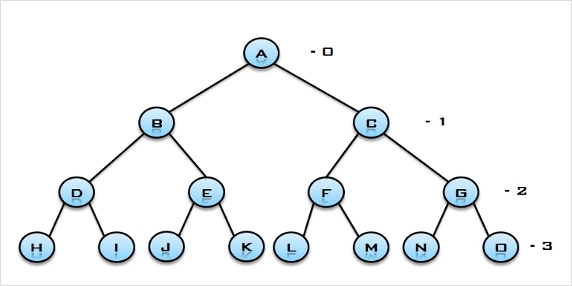
- 포화 이진 트리(Full Binary Tree)
- 높이 h 인 이진 트리에서 모든 단말 노드가 레벨 h 에 있는 트리
- 최대 노드 수 :
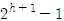
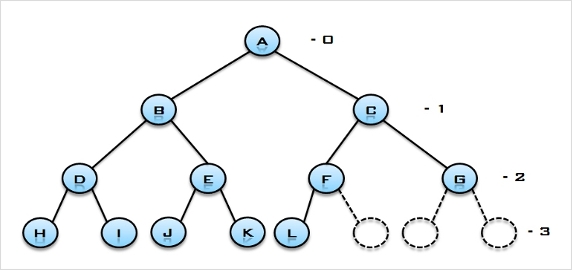
- 완전 이진 트리(Complete Binary Tree)
- 높이(h-1)까지는 포환 이진트리 이고, 마지막 레벨 h에서, 왼쪽에서 오른쪽으로 단말 노드를 채운 것
- 편향 이진 트리(Skewed Binary Tree)
- 이진 트리 중에서 최소 개수의 노드를 가지면서 왼쪽이나 오른쪽 서브 트리만 가지고 있는 트리
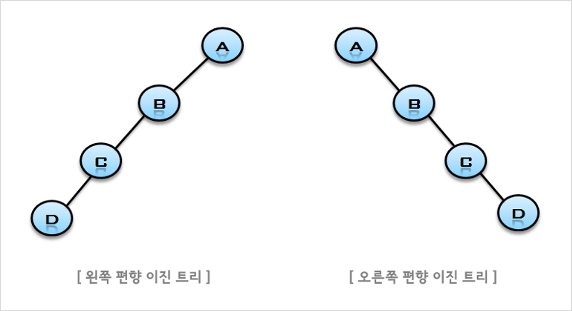
- 이진 트리의 순차 자료구조 표현
- 완전 이진 트리의 배열 표현 방법
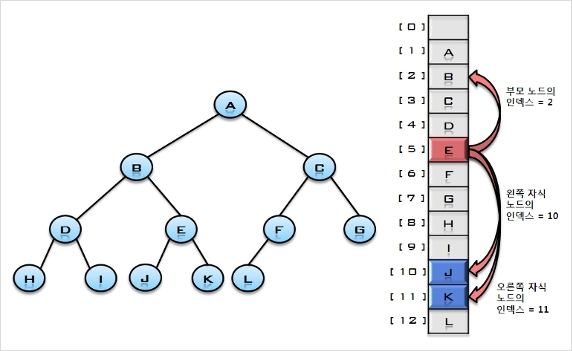
- 이진 트리의 순차 자료구조 표현
- 편향 이진 트리의 배열 표현 방법
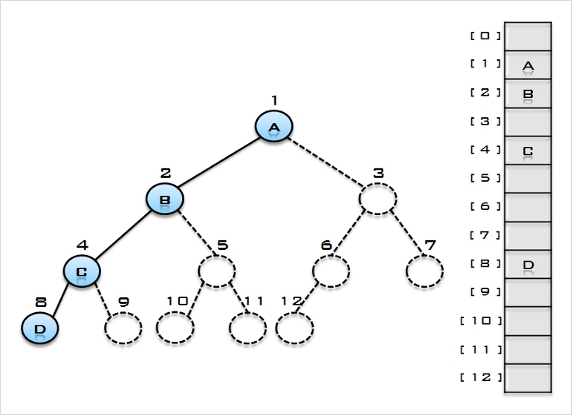
그럼 이제 힙(Heap)에 대해서 알아 보자.
- 힙(Heap)
- 완전 이진 트리에 있는 노드 중에서 키 값이 가장 큰 노드나 키 값이 가장 작은 노드를 찾기 위해서 만든 자료구조
- 최대 힙(Max Heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 항상 크거나 같은 크기의 관계
- ( 부모 노드의 키 값 ≥ 자식 노드의 키 값 ) 의 관계를 가지는 노드들의 완전 이진 트리 - 최소 힙(Min Heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 항상 작거나 같은 크기의 관계
- ( 부모 노드의 키 값 ≤ 자식 노드의 키 값 ) 의 관계를 가지는 노드들의 완전 이진 트리 - 힙(Heap)의 예
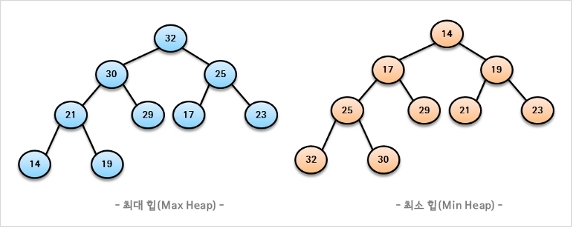
- 힙(Heap)이 아닌 예
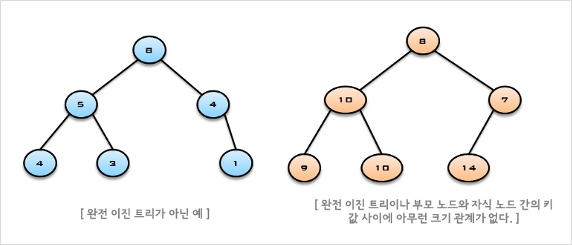
- 힙 정렬(Heap Sort)의 개념
- 힙 자료구조를 이용한 정렬 방법
- 힙(Heap)에서 항상 가장 큰 원소가 루트 노드가 되고 삭제 연산을 수행하면 항상 루트 노드의 원소를 삭제하여 반환
- 최대 힙에서 대해서 원소의 개수만큼 삭제 연산을 수행하여 내림차순으로 정렬 수행
- 최소 힙에 대해서 원소의 개수만큼 삭제 연산을 수행하여 오름차순으로 정렬 수행
- 힙 정렬(Heap Sort) 수행 방법
1. 정렬한 원소들을 입력하여 최대 힙 구성
2. 힙에 대하여 삭제 연산을 수행하여 얻은 원소를 마지막 자리에 배치
3. 나머지 원소에 대해서 다시 최대 힙로 재구성
원소의 개수만큼 2~3을 반복 수행
- 힙 정렬 수행 과정
- 정렬되지 않은 [69, 10, 30, 2, 16, 8, 31, 22]의 자료들을 힙 정렬 방법으로 정렬하는 과정을 살펴보자.
- 초기 상태 : 정렬할 원소가 8개 이므로 노드가 8개인 완전 이진 트리를 만들고, 최대 힙(Max Heap)으로 구성함
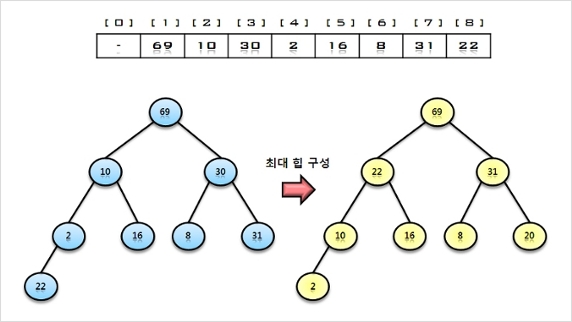
(최대힙 구성시 우측 서브트리의 숫자 20 >> 30 임을 알려드립니다.)
1. 힙에 사제 연산을 수행하여 루트 노드의 원소 69를 구해서 배열의 마지막 자리에 저장한다.
나머지 원소들에 대해서 최대 힙으로 재 구성함
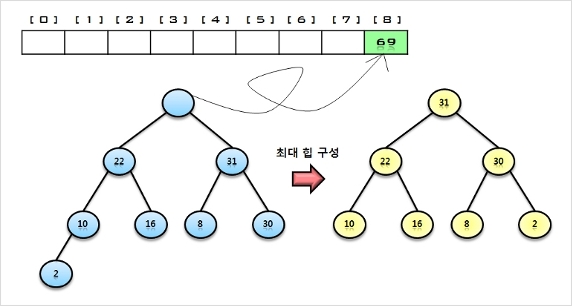
2. 힙에 삭제 연산을 수행하여 루트 노드의 원소 31을 구해서 배열의 비어있는 마지막 자리에 저장한다.
나머지 원소들에 대해서 최대 힙으로 재 구성함
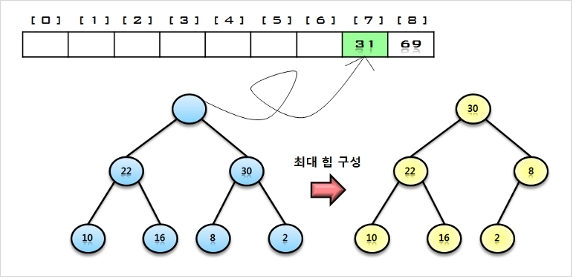
3. 힙에 삭제 연산을 수행하여 루트 노드의 원소 30을 구해서 배열의 비어있는 마지막 자리에 저장한다.
나머지 원소들에 대해서 최대 힙으로 재 구성함
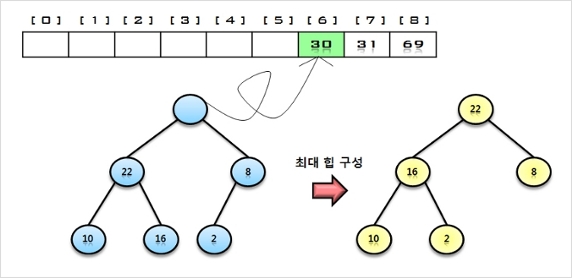
4. 힙에 삭제 연산을 수행하여 루트 노드의 원소 22를 구해서 배열의 비어있는 마지막 자리에 저장한다.
나머지 원소들에 대해서 최대 힙으로 재 구성함
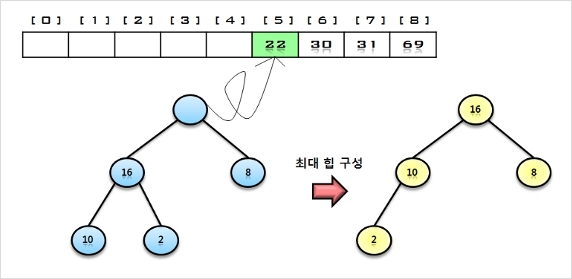
5. 힙에 삭제 연산을 수행하여 루트 노드의 원소 16을 구해서 배열의 비어있는 마지막 자리에 저장한다.
나머지 원소들에 대해서 최대 힙으로 재 구성함
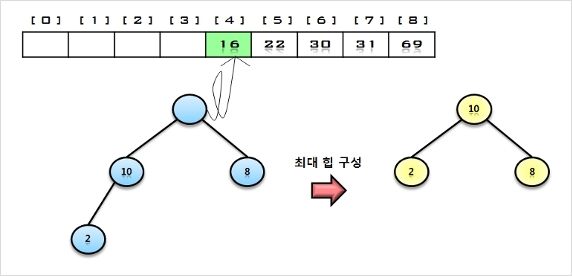
6. 힙에 삭제 연산을 수행하여 루트 노드의 원소 10을 구해서 배열의 비어있는 마지막 자리에 저장한다.
나머지 원소들에 대해서 최대 힙으로 재 구성함
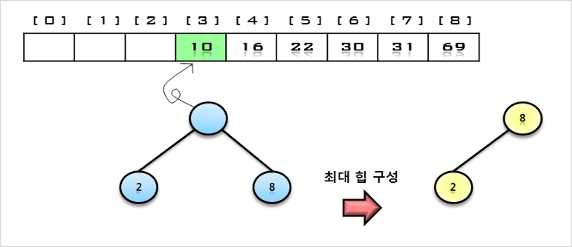
7. 힙에 삭제 연산을 수행하여 루트 노드의 원소 8을 구해서 배열의 비어있는 마지막 자리에 저장한다.
나머지 원소들에 대해서 최대 힙으로 재 구성함
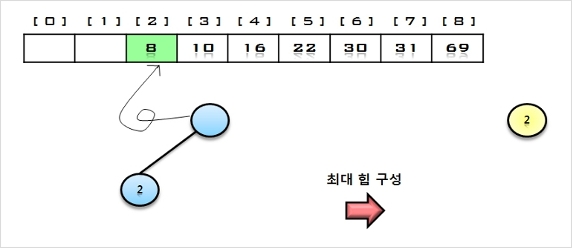
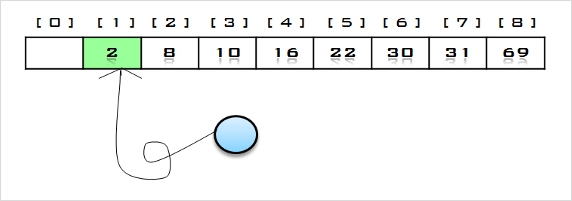
8. 힙에 삭제 연산을 수행하여 루트 노드의 원소 2을 구해서 배열의 비어있는 마지막 자리에 저장한다.
나머지 원소들에 대해서 최대 힙으로 재 구성함
- 힙 정렬 알고리즘 분석
- 메모리 사용공간
- 원소 n개에 대해서 n개의 메모리 공간 사용
- 크기 n의 힙 저장 공간
- 연산 시간
- 힙 재구성 연산 시간
- n개의 노드에 대해서 완전 이진 트리는 log₂(n+1)의 레벨을 가지므로 완전 이진 트리를 힙으로 구성하는 평균 시간은 O(log n)
- n개의 노드에 대해서 n번의 힙 재구성 작업 수행 - 평균 시간 복잡도 : O(n log n)
[출처] 정렬 알고리즘 - 힙 정렬(Heap Sort)|작성자 열쓰
'알고리즘 & 자료구조 > 알고리즘&자료구조' 카테고리의 다른 글
| 빅오표기법/빅오분석법(Big O Notation) (0) | 2012.10.31 |
|---|---|
| 힙(Heap) 트리와 정렬 (우선순위 큐) (0) | 2012.10.31 |
| 해쉬, 해쉬테이블, 정적해쉬, 동적 해쉬 (0) | 2012.10.31 |
| 버튼입력 이벤트처리 (0) | 2012.10.31 |
| 컨볼루션 Convolution (0) | 2012.10.27 |
