투본 IK 는 3개의 조인트를 갖고 IK 를 구하는 방식이다
(언리얼에서의 정의 : 투 본 IK 를 사용해서 3 조인트 체인에 IK 를 적용하는 법입니다.
Two Bone IK (투 본 IK) 컨트롤은 캐릭터의 사지와 같은 3 조인트 체인에 Inverse Kinematics(역운동학, IK)를 적용합니다.)
투본 IK 의 경우 본 3개로 IK 를 구현 하는데 중간 조인트가 어느 방향쪽으로 걲일지에 대한 기준있게 되고
이 기준 위치를 따라 중간 본이 어떤 방향으로 꺽일지가 정해지게 된다
(무기/총 잡을 때 등에 쓰일 수 있다)
IK Bone : 컨트롤할 본 이름, IK 에 의해 컨트롤 되는 메인 본 체인 : 오른 손을 선택
Joint Target : 오른쪽 어깨를 선택 해 놓고
2본 IK(Two Bone IK) 노드엣 Joint Target Location 의 위치를 바꾸면 그 위치 기준으로 하여
꺽을 방향이 역으로 생기게 된다
아래 이미지는 Joint Target Location 을 캐릭터가 바라보는 앞쪽으로 뺏을때 팔이 역으로 꺽이는 형태이고
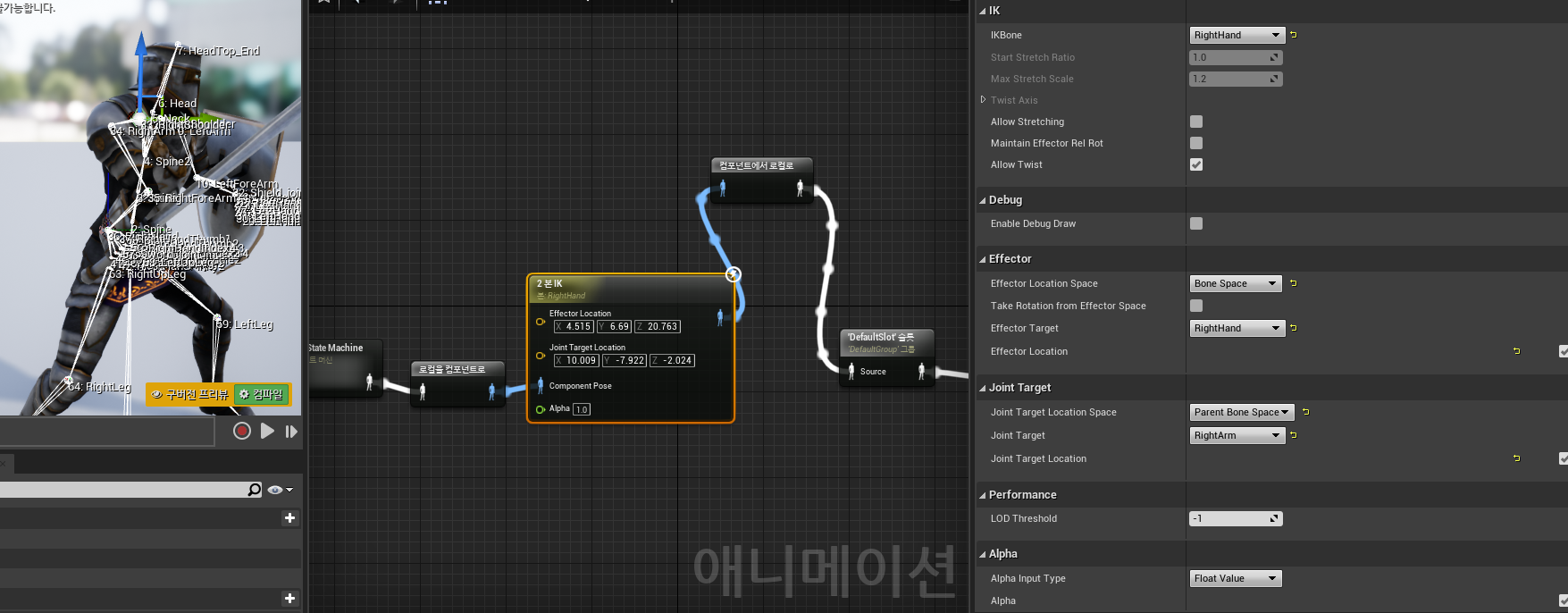
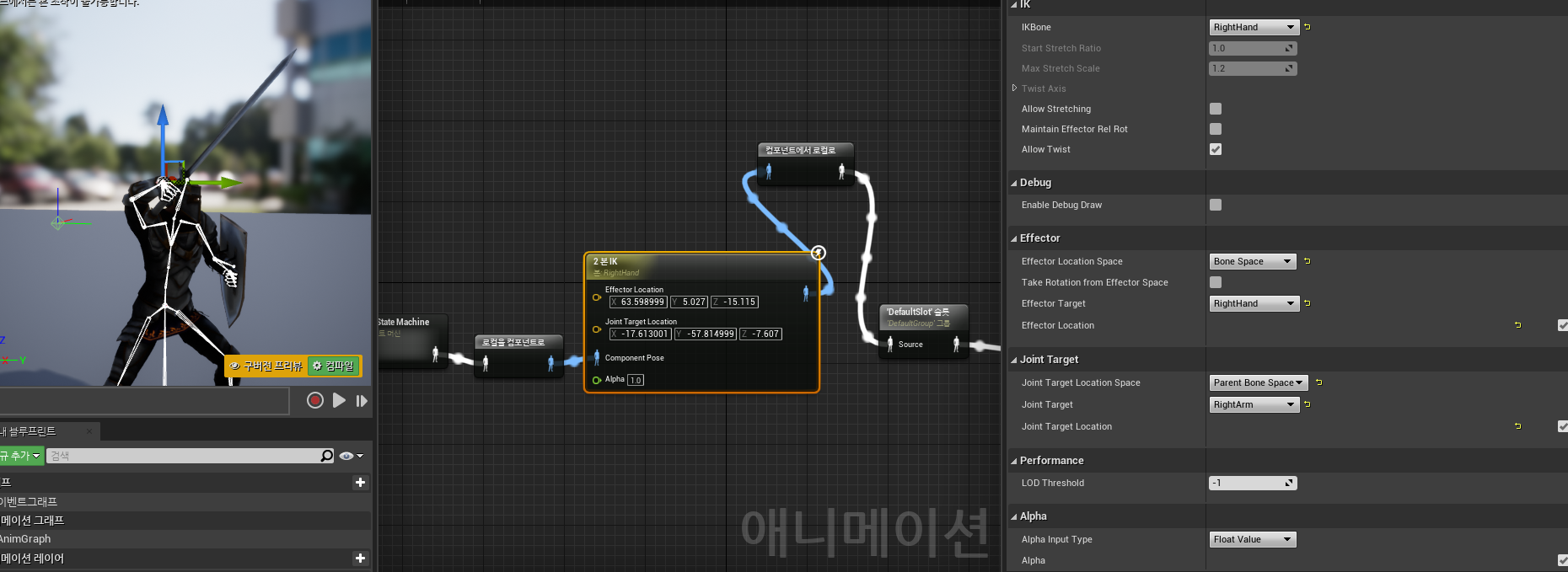
Joint Target Location 를 음수로 하면 즉 캐릭터의 뒤쪽에 배치를 시키면

바르게 팔이 꺽이는 것을 볼 수 있다
이 상태에서
Effector Location 위치를 바꾸면 right hand 가 대상을 따라간다
Analytic Two-Bone IK in 2D
December 29, 2008

Due to their complexity, inverse kinematics (IK) problems are often solved with iterative solutions. While iterative solutions can handle different IK poblems with a single algorithm, they can also become computationally expensive. If a specific IK problem needs to be computed often, it is worth considering an analytic solution.
If we limit the problem to a two bone chain in a two-dimensions, we can derive the anaytic solution without much complexity. This will generally be more efficient than its iterative alternatives. While this specific case lends itself to a 2D world, it can also be used in 3D as long as the kinematic chain's motion is limited to a single plane.
The goal of is to create a robust function with the following requirements.
- Let the user specify which direction to bend the bone chain (there can be up to two valid solutions, each bending in an opposite direction).
- Notify the user when there was no valid solution based on the input.
- When there is no valid solution, calcualte the closest alternative.
- Produce the expected results for every target position. Most implementations found online or in books only function properly when the target is in a certain quadrant or when it remains in a specific range.
If you aren't interested in the exciting math ahead, jump to the end of the article for sample code. You can also download the RJ_Demo_IK application and source code to see a running implementation. If you're the type that likes to know how things work (like me), we will walk through the derivation in detail. It might look extensive at first, but it's only because I've broken it down step by step. Hopefully you'll be able to follow along without much difficulty.
You might also be interested in the following articles on different IK solvers:
원점에 조인트 하나와 중간에 꺽인(θ2 앞에) 조인트 그리고 대상으로할 Target 지점 (x,y) 이렇게 3개가 주어지고
거리 d1, d2 가 주어진다
그리고 원점에서부터 target 까지의 거리 h 로 놓을 수 있는데
Two bone ik 는 figure1 의 도형을 보면 θ2, θ1 을 구하는 것으로 좁혀진다
아래의 유도 과정은 삼각함수들을 통해 구하는 과정으로 먼저 θ2 를 구한 다음 이를 토대로 θ1을 구해 나가는 방식이고
d1 과 d2 거리의 차의 거리까지가 target 으로 접근하는 최소 거리 d1+d2 의 거리가 target 으로 향할 수 있는 최대 거리이며 target 으로 향할수 있을때 target 점 까지의 각도를 두개의 각도 θ2, θ1 를 구할 수 있지만 그 외의서는
벌을 최대한 뻗어 Target 으로 향하는 방향을 가리키게 된다는 유도 과정이다
Defining the problem
Our problem domain consists of a two bone chain where bone1 is located at the origin and bone2 is a child of bone1. Each bone conistis of an angle θ and a distance dd. The goal is to get the end of bone2 to line up with the target point (x,y). Because we have set bone1 at the origin, you will need to transform your destination point relative to bone1. Figure 1 shows how our variables fit together. The distance from the orgin to the target point is defined as hh.

figure 1
The solvable domain


figure 2
Math review
Before we hop into the derivation, I want to review a few trigonometric identities that we will be using. For more information on the identities, Wikipedia has an extensive list and also has a page on the derivations.

Solving for θ2

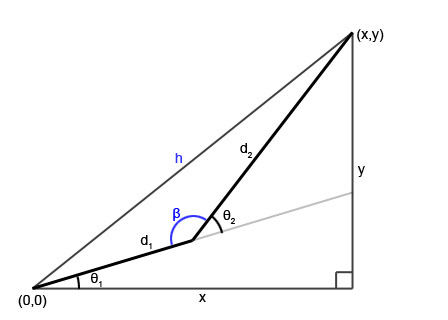
figure 3

We now have our analytic equation for θ2, but there are a few nuances to discuss in more detail.
- theta2 기준으로 봤을 때 d1 과 d2 가 회전 되어서 구부러지는 것을 생각해보면 되는데 theta2가 -1이면 d1 과 d2 가 펴지고, theta2 가 1 이면 d1 과 d2 가 최대로 구부러지게 된다
If cosθ2 is not within the range [-1,1], it is outside of the arccosθ domain. This will happen when our target point is a location the bones cannot reach. A value of -1 will give us an angle of 180° (i.e. bone2 is fully bent) and a value of 1 will give us an angle of 0° (i.e. bone2 is fully extended). When the value is less than -1, our bone is trying to bend father than is physically possible to reach a point that is too close to the origin. When the value is greater than 1, our bone is trying to extend farther than is physically possible to reach a point that is too far from the origin. This means that we can compute the best non-valid solution by clamping the value into the legal [-1,1] range. - If d1 or d2 is zero, we will divide by zero when computing cosθ2. When one or both bones have a zero length, we can set θ2 to any value we desire (I suggest zero or the value used on a previous frame). When we solve for θ1 it will correct itself according to our selected θ2. The solvable domain for this case has also been reduced to a single circle centered at the origin with a radius of d1+d2.
- When we can evaluate arccosθ, our result is limited to the range [0,π]. If we use the result as is, we will always find the solution where our second bone turns in the positive direction. If it is our intention to find the solution that bends in the negative direction, we need to negate the new θ2.
(theta2 기준으로 보면
Solving for θ1


figure 4

여기서 tan 공식을 보면
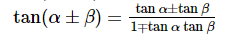
이런 형태가 있는데 이것을 이용하여 다음처럼 전개한다

Writing the code
We can now write our algorithm in code. The function will calculate a valid IK solution if possible. If there is no valid solution, it will calculate one that gets the end of bone2 as close to the target as possible. Check out the RJ_Demo_IK application for a functional implementation of this code.
These code samples are released under the following license.
/******************************************************************************
Copyright (c) 2008-2009 Ryan Juckett
This software is provided 'as-is', without any express or implied
warranty. In no event will the authors be held liable for any damages
arising from the use of this software.
Permission is granted to anyone to use this software for any purpose,
including commercial applications, and to alter it and redistribute it
freely, subject to the following restrictions:
1. The origin of this software must not be misrepresented; you must not
claim that you wrote the original software. If you use this software
in a product, an acknowledgment in the product documentation would be
appreciated but is not required.
2. Altered source versions must be plainly marked as such, and must not be
misrepresented as being the original software.
3. This notice may not be removed or altered from any source
distribution.
******************************************************************************/
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
|
///***************************************************************************************
/// CalcIK_2D_TwoBoneAnalytic
/// Given a two bone chain located at the origin (bone1 is the parent of bone2), this
/// function will compute the bone angles needed for the end of the chain to line up
/// with a target position. If there is no valid solution, the angles will be set to
/// get as close to the target as possible.
///
/// returns: True when a valid solution was found.
///***************************************************************************************
public static bool CalcIK_2D_TwoBoneAnalytic
(
out double angle1, // Angle of bone 1
out double angle2, // Angle of bone 2
bool solvePosAngle2, // Solve for positive angle 2 instead of negative angle 2
double length1, // Length of bone 1. Assumed to be >= zero
double length2, // Length of bone 2. Assumed to be >= zero
double targetX, // Target x position for the bones to reach
double targetY // Target y position for the bones to reach
)
{
Debug.Assert(length1 >= 0);
Debug.Assert(length2 >= 0);
const double epsilon = 0.0001; // used to prevent division by small numbers
bool foundValidSolution = true;
double targetDistSqr = (targetX*targetX + targetY*targetY);
//===
// Compute a new value for angle2 along with its cosine
double sinAngle2;
double cosAngle2;
double cosAngle2_denom = 2*length1*length2;
if( cosAngle2_denom > epsilon )
{
cosAngle2 = (targetDistSqr - length1*length1 - length2*length2)
/ (cosAngle2_denom);
// if our result is not in the legal cosine range, we can not find a
// legal solution for the target
if( (cosAngle2 < -1.0) || (cosAngle2 > 1.0) )
foundValidSolution = false;
// clamp our value into range so we can calculate the best
// solution when there are no valid ones
cosAngle2 = Math.Max(-1, Math.Min( 1, cosAngle2 ) );
// compute a new value for angle2
angle2 = Math.Acos( cosAngle2 );
// adjust for the desired bend direction
if( !solvePosAngle2 )
angle2 = -angle2;
// compute the sine of our angle
sinAngle2 = Math.Sin( angle2 );
}
else
{
// At least one of the bones had a zero length. This means our
// solvable domain is a circle around the origin with a radius
// equal to the sum of our bone lengths.
double totalLenSqr = (length1 + length2) * (length1 + length2);
if( targetDistSqr < (totalLenSqr-epsilon)
|| targetDistSqr > (totalLenSqr+epsilon) )
{
foundValidSolution = false;
}
// Only the value of angle1 matters at this point. We can just
// set angle2 to zero.
angle2 = 0.0;
cosAngle2 = 1.0;
sinAngle2 = 0.0;
}
//===
// Compute the value of angle1 based on the sine and cosine of angle2
double triAdjacent = length1 + length2*cosAngle2;
double triOpposite = length2*sinAngle2;
double tanY = targetY*triAdjacent - targetX*triOpposite;
double tanX = targetX*triAdjacent + targetY*triOpposite;
// Note that it is safe to call Atan2(0,0) which will happen if targetX and
// targetY are zero
angle1 = Math.Atan2( tanY, tanX );
return foundValidSolution;
}
|
ref : http://www.ryanjuckett.com/programming/analytic-two-bone-ik-in-2d/
'게임엔진(GameEngine) > Unreal4' 카테고리의 다른 글
| 회전 및 이동 처리에 사용되는 함수들 (0) | 2020.05.24 |
|---|---|
| TSubclassOf, TEnableIf, TPointerIsConvertibleFromTo 의 이해 (0) | 2020.05.21 |
| CCD IK (Cylic Coordinate Descent IK ) : IK (0) | 2020.05.06 |
| FABRIK Algorithm : IK (0) | 2020.05.05 |
| Calling Blueprints in the Editor (0) | 2020.04.27 |
