첨부파일 :
이하 퍼온글
라플라스 변환(Laplace transform)은 어떠한 함수 f(t)에서 다른 함수로의 변환으로, 선형 동역학계와 같은 미분 방정식을 풀 때 유용하게 사용된다. 피에르시몽 라플라스의 이름을 따 붙여졌다.
라플라스 변환을 이용하면, 어려운 식들을 쉽게 변환하여 풀 수 있으며, 문제들을 직접적으로 해결 할 수 있는 장점이 있다. 초기값 문제의 경우 일차적으로 일반해를 구하는 단계가 필요없게 되고, 비제차 미분방정식의 경우에는 대응하는 제차미분방정식을 먼저 풀 필요가 없다. 라플라스 변환은 주어진 식은 간단한 식으로 변환한 뒤, 변형된 식을 푼다. 그리고 그렇게 풀어진 해를 다시 원식으로 변환한다.
라플라스 변환 : t 관련 값이 들어가 s 관련 값이 나온다
정의
함수 f(t)의 라플라스 변환은 모든 실수 t ≥ 0 에 대해, 다음과 같은 함수 F(s)로 정의된다.
여기서 0 − 는  를 간단히 나타낸 것이고 복소수
를 간단히 나타낸 것이고 복소수  , σ와 ω는 실수이다.
, σ와 ω는 실수이다.
실제 사용시에는 엄밀히 정확하지는 않지만  로 표기하기도 한다.
로 표기하기도 한다.
위 정의대로 풀때 무한대 기호가 있기 때문에 이상적분으로 풀이를 하지만 간편하게 그렇다고 인지하고 있고 그냥
풀어 나간다, 너무 자세한건 오히려 보기 지저분할 수 있다
성질
선형성
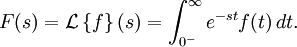
미분
 = sF(s) - f(0)
= sF(s) - f(0) = s^2F(s) - sf(0) - f'(0)
= s^2F(s) - sf(0) - f'(0)
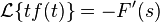 = - d/ds F(s)
= - d/ds F(s)
t^2 라면
- ( - ) d/ds d/ds F(s) = + d^2/ds^2 F(s)
 = (-1)^n d^n/ds^n F(s)
= (-1)^n d^n/ds^n F(s)- 'L{ } ' is laplace
 , L{ f(t) } = F(σ)
, L{ f(t) } = F(σ)
적분- '*' is convolution , "합성곱"
- tip : T is not t
- L { 1 * f(t) } =

합성곱 ( '*' is convolution , "합성곱" )
(f * g)(t) = ∫ f(u)g(t-u) du , 적분범위는 0(아래 끝) ~ t(위 끝) 까지

t shifting- u( t - a) = 단위계단 함수(= 층계 함수)
- t <= a 라면 u(t-a) = 0
- t > a 이면 u(t-a) = 1
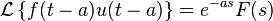
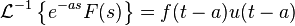
참고: u(t)는 층계 함수이다.
합성곱
주기가 p인 주기함수의 라플라스 변환
- 라플라스 역변환( s 관련 값이 들어가 t 관련 값이 나온다 )
이를 이용하면 위 예제들 역시 간단히 그 해를 찾을 수 있습니다.
'수학 (Mathematics) > 공업수학' 카테고리의 다른 글
| 적분 12 : 고급 정적분 테크닉 - 미분 (1) (0) | 2012.11.03 |
|---|---|
| 단위계단함수 (0) | 2012.11.03 |
| 비선형 미분방정식 [기초] (0) | 2012.11.03 |
| 비감쇠 강체운동 미분방정식(상계수미방-미정개수법으로 풀이) (0) | 2012.11.03 |
| 치환을 활용한 비동차(비제차) 미분방정식 ( 코시 오일러 미방, 매개변수변환법 ) (0) | 2012.11.03 |



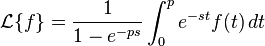














 Laplace Transform -3.pdf
Laplace Transform -3.pdf
