(1) 역수관계
|
삼각함수 미분
!! 앞에 c 로 시작하는 것을 미분하면 - 로 나온다
(sin(x))'=cos(x)
(cos(x))'=-sin(x)
(tan(x))'=ses^2(x)
cos^2(x) + sin^2(x) =1
역삼각함수(inverse trigonometric function)이란 삼각함수의 역함수를 말한다. 삼각함수는 단사함수가 아니기 때문에 이의 역함수를 정의하려면 정의역을 제한하는 것이 필요하다. 아래는 역삼각함수들의 정의와 표기법, 정의역과 치역들을 나타낸 표이다.
역 삼각함수의 도함수
자세한 증명은 아래에..
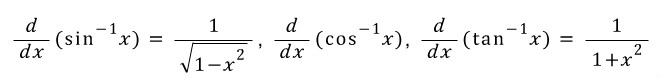
arccos'(x) = -1/sqrt(1-x^2)
arcsin 정의역 (-1,1) ==> -1,1은 포함되지 않는다
arcsin 정의역 [-1,1]
arctan 정의역 -∞ , ∞
1) y=arcsin(1-x)
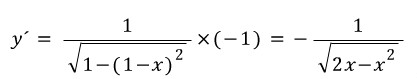
2) y=arccos(root[x])
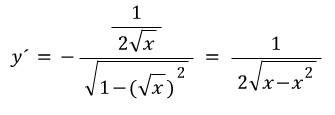
3) y=arctan(x^2)
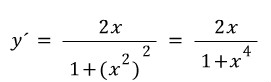
http://blog.naver.com/mindo1103/90095392364
역삼각함수 도함수 인강
http://blog.naver.com/proyjh426?Redirect=Log&logNo=120119010835
반응형
'수학 (Mathematics) > 미적분학' 카테고리의 다른 글
| 다변함수 미분, 전미분, 전도함수 편도함수 증명정리 (1) | 2012.11.03 |
|---|---|
| 엡실론-델타 논법 (ε - δ)과 Δy = f(x+Δx) - f(x) = ( f'(x) + ε )Δx 의 관계와 dy (0) | 2012.11.03 |
| 어떤 다변함수극한 증명과 일변함수의 형태 (0) | 2012.11.03 |
| 지수함수 로그함수의 도함수 (0) | 2012.11.03 |
| 미분의 d 의 실체 d /dx & dY = Y'dx (0) | 2012.11.03 |




