행렬식

---

http://blog.naver.com/rlawldyd0806/50036277924

행렬식

-행과 열이 같은 정방 행렬에서만 구할 수 있다

정방 행렬 A에 대한 행렬식 표현

detA = det(A) = |A|

 

행렬식을 계산하기 위해 필요한 두 가지 개념

1. 소행렬식(minor)이라는 것으로, (i, j)소행렬식 M_ij 는 nXn정방 행렬A에서i번째행과

    j번째 열을 제외한 (n-1)X(n-1) 정방 행렬의 행렬식을 의미

2. 여인자(cofactor)라는 것으로 A­_ij = (-1)^i+jM­_ij로 표현

 

소행렬식 및 여인자 예)

 가 주어졌을 때, 여인자 A­₁₂ 와 A­₃₁은?

여인자 식에 대입하면 A­₁₂ = (-1)¹⁺²M­₃₁와 A­₃₁ = (-1)³⁺¹M­₃₁된다.

 

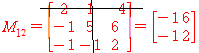소행렬식  M­₁₂  

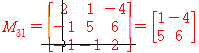소행렬식 M­₃₁  

 여인자  여인자

 

D3DX함수

여인자를 구하는 함수는 지원하지 않는것 같다.

 

사용자함수

//소행렬식을 구하여 여인자 구한다.

D3DXMATRIX *MYMatrixCofactor(D3DXMATRIX *pOut, D3DXMATRIX *pMat)
{
 pOut->_11 = (pMat->_22 * pMat->_33 - pMat->_23 * pMat->_32);
 pOut->_12 = -(pMat->_21 * pMat->_33 - pMat->_23 * pMat->_31);
 pOut->_13 = (pMat->_21 * pMat->_32 - pMat->_22 * pMat->_31);

 pOut->_21 = -(pMat->_12 * pMat->_33 - pMat->_13 * pMat->_32);
 pOut->_22 = (pMat->_11 * pMat->_33 - pMat->_13 * pMat->_31);
 pOut->_23 = -(pMat->_11 * pMat->_32 - pMat->_12 * pMat->_31);

 pOut->_31 = (pMat->_12 * pMat->_23 - pMat->_13 * pMat->_22);
 pOut->_32 = -(pMat->_11 * pMat->_23 - pMat->_13 * pMat->_21);
 pOut->_33 = (pMat->_11 * pMat->_22 - pMat->_12 * pMat->_21);

 return pOut;
}

 

여인자를 이용한 행렬식 표현

동일한 열 성분(a_1j, a_2j, •••, a_nj)에 대해서 표현

 

 

동일한 행 성분(a_j1, a_j2, •••, a_jn)에 대해서 표현

 

 

1X1정방 행렬  A=[a]의 행렬식 |A|=a

 

2X2정방 행렬 의 행렬식 계산

 

2X2정방 행렬식은 대각선 성분의 곱(a₁₁a₂₂)을 비대각선 성분의 곱(a₁₂a₂₁)으로 뺀 모양이다

 

3X3정방 행렬의 행렬식

       

    

 

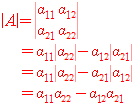
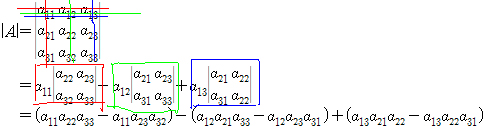
 Direct3D 함수

FLOAT D3DXMatrixDeterminant(CONST D3DXMATRIX *pM);

 

사용자 함수

//행렬의 행렬식을 구한다.

float MYMatrixDeterminant(D3DXMATRIX *pM)
{
 return (pM->_11*pM->_22*pM->_33) + (pM->_12*pM->_23*pM->_31) + (pM->_13*pM->_21*pM->_32)
      - (pM->_11*pM->_23*pM->_32) - (pM->_12*pM->_21*pM->_33) - (pM->_13*pM->_22*pM->_31);
}