☆ 더 쉽게 - 선 교차 판정 - ☆
여기에서는 선분 교차 판정의 정석이라 할 방법을 소개하고 있습니다.
선분과 직선 간과 소중한 정의입니다.
직선은 한 2 점을지나는선이고
선분은 한 2 점을연결하는선이다.
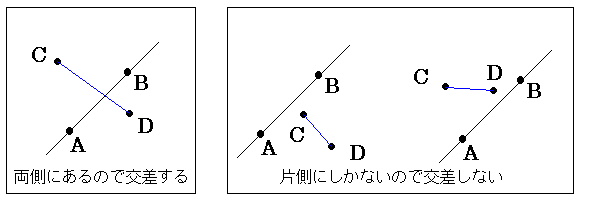
교차 판정에 대한 점 A, B, C, D, 선분 AB와 선분 CD의 교차를 생각하고 있습니다. 먼저 '선 교차 판정'의 전통적인
"교차점을 찾아 그 교차점이 2 개의 세그먼트의 범위에 있는지 조사한다"
라는 생각을 다른 해석으로 바꿉니다.
2 선이 교차하고있다는 것은"점 A, B를 지나는 직선이 선분 CD와 교차하며
점 C, D를 지나는 직선이 선분 AB와 교차하고있다 "
로 해석할 수 있습니다. 그래서 선과 선의 교차점은 다음과 같이 확인합니다."선을 경계로 선분을 구성하는 2 가지 사항이
직선에 양쪽에 존재할 때, 직선과 선분은 교차한다 "그런 다음 그 점이 직선에 대해 어느 편에있는지를 묻는 방법을 알아보겠습니다.
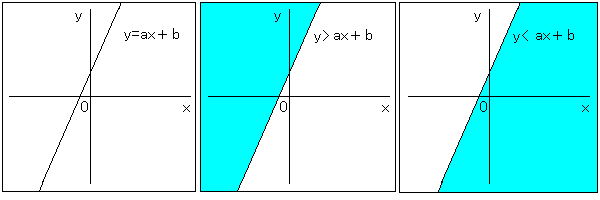
y = ax + b라는 직선 =를 부동로 대체
y> ax + b, y <ax + b라는 영역을 나타내는식이 있었다면, 이들 3 개식이 그려진 도형 영역은 다음과 같이 나타낼 수 있습니다.여기서 2 개의 식을 왼쪽에 移項하여 y - ax - b> 0
y - ax - b <0
로 할 수 있습니다. 있는 점이 직선에 대해 어느 편에 있는지 필요하다면 직선의 방정식에 그 문제에 관해서 (X, Y)를 할당하고 결과 얻어진 값이 양수인지 음수인지에 따라 알 수 있습니다. 양의 경우 한 지점은 직선의 위쪽에 음수이면 한 지점은 직선의 아래 부분에 위치한다는 것을 알 수 있습니다. 직선의 양쪽 (위쪽과 아래쪽)에 점이 있으면 교차하기 때문에, 직선과 선분의 교차 판정을 위해서는 선분을 구성하는 2 개의 점을 직선의 방정식에 대입하여 얻은 값 부호가 서로 다른 (혹은 0) 여부를 조사하면 좋은 것입니다. 다른 경우에 (서로를 곱한 <0) 교차하고 있다고 판정할 수 있습니다.
이것을 구체적으로 식 화해보십시오.
점 A, B의 좌표를 A (x1, y1), B (x2, y2) 로,이 2 가지를 지나는 직선과
점 C, D의 좌표, C (x3, y3), D (x4, y4) 을 잇는 선분을 생각합니다.
점 A (x1, y1), B (x2, y2)를 지나는 직선 AB의 방정식은y = x * (y1 - y2) / (x1 - x2) + y1 - x1 * (y1 - y2) / (x1 - x2)
로 나타낼 수 있습니다. 나눗셈은 0으로 나누기 또는 오버플로가 무서워 위해 피하기 때문에, 양변에 (x1 - x2)를 걸고 다음과 같이 변형합니다.y * (x1 - x2) = x * (y1 - y2) + y1 * (x1 - x2) - x1 * (y1 - y2)
이것을 더욱 단순화하고, 왼쪽에 수집합니다.(x1 - x2) * (y - y1) + (y1 - y2) * (x1 - x) = 0
이것은 점 A (x1, y1), B (x2, y2)를 지나는 직선의 방정식입니다.
이제이 방정식에 점 C (x3, y3), D (x4, y4)을 할당하고 그 부호를 검사하여 직선과 선분의 교차 판정을 할 수 있습니다.
점 C를 할당tc = (x1 - x2) * (y3 - y1) + (y1 - y2) * (x1 - x3) 점 D를 할당td = (x1 - x2) * (y4 - y1) + (y1 - y2) * (x1 - x4)
교차 = 2 개의 식의 부호가 다르다는 것을 수식으로 표현하면,tc * td <0
과 같습니다 다음 코드로 판정 가능합니다. 시저하면 1 줄은 모르지만,
생각 자체는 One Line입니다.
'구조 Private Type POINT x As Double y As Double End Type '좌표 p1, p2을 지나는 직선과 좌표 p3, p4을 잇는 선이 교차하는지 확인 Private Function intersect (p1 As POINT, p2 As POINT, P3 As POINT, p4 As POINT) as Boolean If (((p1.x - p2.x) * (p3.y - p1.y) + (p1.y - p2.y) * (p1.x - p3. x)) * _ ((p1.x - p2.x) * (p4.y - p1.y) + (p1.y - p2.y) * (p1.x - p4.x))> 0 #) Then '교차하지 않는 intersect = False Exit Function End If '교차 intersect = True End Function
그리고, 선분 AB와 직선 CD에 대해서도 같은 조사를 사용하여 ta = (x3 - x4) * (y1 - y3) + (y3 - y4) * (x3 - x1)
tb = (x3 - x4) * (y2 - y3) + (y3 - y4) * (x3 - x2)
ta * tb <0
위와 함께, 2 가지 조건 판정하는 경우, 2 개의 선분의 교차 판정을 할 수 있습니다.
'구조 Private Type POINT x As Double y As Double End Type '좌표 p1, p2를 잇는 선과 좌표 p3, p4을 잇는 선이 교차하는지 확인 '그러나 선이 겹치는 경우 ( 3 점, 4 점이 일직선상에있다), "교차하고 있지 않다"라고 판정합니다. Private Function intersection (p1 As POINT, p2 As POINT, P3 As POINT, p4 As POINT) as Boolean If (((p1.x - p2.x) * (p3.y - p1.y) + (p1.y - p2.y) * (p1.x - p3.x)) * _ ((p1.x - p2.x) * (p4.y - p1.y) + (p1.y - p2.y) * (p1 x - p4.x)) "0 #) Then If (((p3.x - p4.x) * (p1.y - p3.y) + (p3.y - p4.y) * (p3.x - p1.x)) * _ ((p3.x - p4.x) * (p2.y - p3.y) + (p3.y - p4.y) * (p3.x - p2.x)) " 0 #) Then intersection = True Exit Function End If End If intersection = False End Function
이 판정은 선분들이 겹치는 경우 (3 점 또는 4 점이 일직선상에있다), "교차하고 있지 않다"라고 판정합니다. 이것을 "교차한다"고 판정하고 싶은 경우에 대해서는더 빠르고 - 선 교차 판정 -를 참조하십시오. 위의 알고리즘만으로는이를 판정하는 것은 조금 어렵습니다.
(곱셈에 대한 오버플로 및 정수와 부동 소수점)
위 코드는 부동 소수점 연산에서 실시하고 있지만 실제로이 작업을 Windows 그리기 등에 사용하는 경우에는 정수 계산만으로 가능하며, 부동 소수점 대신 Long 정수를 사용하는 것이 빠르게 처리할 수 있기 때문에, 그 쪽이 좋을지도 모릅니다. 만약, 판정하려는 선의 점이 엄청나게 큰 경우, 곱셈에 대한 오버플로가 우려되기 때문에 전체 규모 자체를 작게하여 부동 소수점 계산을 할 필요가 있습니다. 그럴 때 선언하는 변수를 변경하면 유효한이 계산 방법은 아주 편리 뛰어나다고 생각합니다.
아래의 예제에서는 정수 버전을 사용하고 있습니다.
(참고로)
대부분의 참고서이 교차 판정을
"점 A, B를 지나는 직선과 반점 C의 위치 관계에 관하여, ABC 순서별로 점이 시계 방향 또는 시계 반대 방향으로 위치하고있는가라는 것을 알고있다"
와 같이 기술하고 설명하고 있다고 생각합니다. 위의 설명은이 방법을 증명 형식에 가서 보았습니다.
(참조)
'알고리즘 C 제 3 권;
野平 코헤이, 별 군수, 사토 Drug, 타구치 동쪽 공역
현대 과학사
'알고리즘과 데이터 구조』
강촌 준 아키라, 上坂 吉則, 아사 세종 바다, 아리사 마코토, 니시 무라 슌스케
実教出版(샘플 프로그램의 동작 확인)
기종 PC - 9821V13S OS Windows95 개발 도구 Visual Basic Ver.4.0 업데이트 : 00/07/22 다운로드 easyCross.lzh(2.86KB)
Visual Basic Ver.5.0, Ver.6.0 잘 작동한다고 생각합니다.
또한,이 코너에 게재되는 프로그램 코드 및 프로그램 파일로 인해 발생하는 손해 등에 대해서 책임을 질 수 없습니다.
★이 선의 교차는 다양한 작업에 사용할 수 있다고 생각합니다. 본 소스 문서 배포 전재는 금지 입니다만 게재되는 프로그램 코드 및 프로그램 파일은 각자의 책임하에 자유롭게 배포달라고해도됩니다. 그 때, 본 사이트를 소개해 주시면 대단히 기쁩니다.
http://www5d.biglobe.ne.jp/~tomoya03/shtml/algorithm/IntersectionEX.htm
'構造体
Private Type POINT
x As Double
y As Double
End Type
'座標 p1,p2 を結ぶ線分と座標 p3,p4 を結ぶ線分が交差しているかを調べる
'ただし、線分が重なっている場合(3点,4点が一直線上にある)、「交差している」、と判定します。
Private Function intersectionEX(p1 As POINT, p2 As POINT, _
p3 As POINT, p4 As POINT) As Boolean
'x座標によるチェック
If (p1.x >= p2.x) Then
If ((p1.x < p3.x And p1.x < p4.x) Or (p2.x > p3.x And p2.x > p4.x)) Then
intersectionEX = False: Exit Function
End If
Else
If ((p2.x < p3.x And p2.x < p4.x) Or (p1.x > p3.x And p1.x > p4.x)) Then
intersectionEX = False: Exit Function
End If
End If
'y座標によるチェック
If (p1.y >= p2.y) Then
If ((p1.y < p3.y And p1.y < p4.y) Or (p2.y > p3.y And p2.y > p4.y)) Then
intersectionEX = False: Exit Function
End If
Else
If ((p2.y < p3.y And p2.y < p4.y) Or (p1.y > p3.y And p1.y > p4.y)) Then
intersectionEX = False: Exit Function
End If
End If
If (((p1.x - p2.x) * (p3.y - p1.y) + (p1.y - p2.y) * (p1.x - p3.x)) * _
((p1.x - p2.x) * (p4.y - p1.y) + (p1.y - p2.y) * (p1.x - p4.x)) > 0#) Then
intersectionEX = False: Exit Function
End If
If (((p3.x - p4.x) * (p1.y - p3.y) + (p3.y - p4.y) * (p3.x - p1.x)) * _
((p3.x - p4.x) * (p2.y - p3.y) + (p3.y - p4.y) * (p3.x - p2.x)) > 0#) Then
intersectionEX = False: Exit Function
End If
intersectionEX = True
End Function
|
반응형
'수학 (Mathematics) > 3D수학' 카테고리의 다른 글
| 타원 그리기 (0) | 2012.11.02 |
|---|---|
| 원과 선분의 충돌 (0) | 2012.11.02 |
| NDC 공간이란 (0) | 2012.11.02 |
| 베지어 곡선(Bezier Curve) 유도와 설명 (1) | 2012.11.02 |
| 3차 곡선, 에르미트 곡선 도출에서 근사적 좌표프레임까지 얻어내기 (0) | 2012.11.02 |