http://cpu815.blog.me/110035113430
Balanced Binary Search Tree(ex : Red-Black Tree)
역시 매우 중요한 자료구조. 균형 잡힌(!) 이진 탐색 트리는 추가, 삭제, 검색을 모두 로그 시간 O(logn)에 수행할 수 있는 매우 우수한 자료구조이다. 비록 해쉬 테이블 상수 시간에 이루어지지는 않지만,탐색 트리의 장점은 키 값들이 정렬이 되어있다는 것이다. 따라서 위의 전화번호부 예에서 사람 이름에 대해서 소팅을 많이 해야 한다면, 이진 트리를 사용해야 한다.
이진 트리는 아래와 같이 생긴 자료구조이다. 그러나 최악의 경우 모든 원소가 한 쪽에만 달려있다면,이는 리스트와 전혀 다름이 없다.
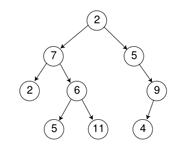
따라서, 양쪽 노드의 개수를 "적절히" 분배를 해주는 것이 가장 중요하다. 만약 똑같이 분배가 되어있다면, 탐색 및 연산 작업이 로그 시간에 수행될 수 있다. 최대 트리의 높이만큼 순회하면 되므로 log 시간이 걸리는 것이다. 이렇게 연산 시간을 로그 시간이 될 수 있도록 보장하는 이진 트리를 Balanced Binary Search Tree라고 부른다. 여기에는 정말로 많은 자료구조가 있으며 해야 할 얘기도 무척 많다. 그러나 대표적인 Red-Black Tree만 얘기해보자.
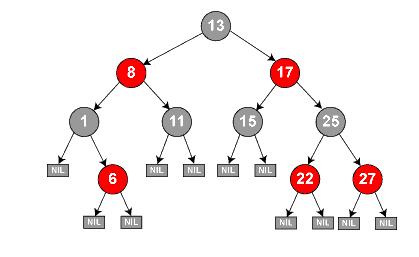
그림에서 보듯이, 각각의 노드에 빨강, 검정색의 속성을 추가한다. 그리고 “빨간 노드의 자식은 모두 검정 노드여야 한다”와 같은 여러 속성을 정하고, 삽입/추가할 때 마다 이 속성이 유지되도록 보정을 해준다. (예: rotation) 그래서 노드가 균형을 유지하도록 한다. Red-Black Tree는 양쪽 노드의 깊이가 서로 두배 이상 차이가 나지 않음을 보장한다.
반면, AVL Tree라고 불리는 녀석은 양쪽 노드의 길이가 최대 하나 밖에 차이가 나지 않도록 한다.훨씬 더 엄격하게 균형을 맞춘다. 따라서 당연히 이 균형을 맞추는 보정 작업에 소요되는 시간이 Red-Black Tree보다 크다.
키와 데이터 쌍을 저장할 때, 검색이 가장 우선 순위라면 당연히 해쉬 테이블을 사용해야 할 것이다.그러나 이 키 값들이 정렬이 되고 싶다면 Red-Black Tree가 가장 좋은 자료구조이다.
정리
형태 | 순서여부 | 색인여부 | 삽입/삭제 도 | 검색속도 | 중복여부 |
List | Yes | No | Fast (constant time) | Slow O(n) | Yes |
Array | Yes | By int (constant time) | Slow O(n) except if inserting at end, in which case constant time | Slow O(n) | Yes |
(Hash)Map | No | By key (constant time) | Fast (constant time) | Fast (constant time) | No (keys) Yes (values) |
Red-Black | Yes | By key O(log n) | Fast O(log n) | Fast O(log n) | No |
[출처] Red-Black Tree|작성자 카푸치노
'알고리즘 & 자료구조 > 알고리즘&자료구조' 카테고리의 다른 글
| 해밀턴회로 (0) | 2012.12.23 |
|---|---|
| 근의 공식 알고리즘 소스코드 (0) | 2012.11.02 |
| 반올림&반내림 함수 , 소수점자리 반올림&반내림 함수 (0) | 2012.10.31 |
| C++ 로 짠 스택 계산기 (0) | 2012.10.31 |
| 그래프 정리 (0) | 2012.10.31 |
