n >= 1
F_n = F_{n-1} + F_{n-2}
F_1 = F_2 = 1
1 1 2 3 5 ....
F_1 F_2 F_3 F_n
n 은 피보나치 수열을 만드는 번째..
int fibonacci(int n){
if( n == 1 || n == 2)
return 1;
return fibonacci( n - 1 ) + fibonacci( n - 2 ) ; // 후위 순회와 유사하다 값을 나중에 리턴 함으로..
}
피보나치수열 참고
참고 : http://blog.naver.com/kwanskim?Redirect=Log&logNo=20110843012
자연계의 피보나치 수열 2010/08/02 05:30 |
피보나치 수열 (Fibonacci Numbers)
1. 피보나치 수열
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …
처음의 두 숫자는 0과 1이고, 그 다음부터는 이전 두 항의 합으로 이루어진다. 첫번째 항 0을 제외하는 경우도 있다.
2. 피보나치와 피보나치 문제
피보나치 (약 1170-1250)는 이탈리아의 수학자로서 <Liber Abaci>라는 책을 통해 힌두-아라비아 숫자 체계를 유럽에 전파한 것으로도 잘 알려져 있는 중세 유럽의 최고 지성이다. 또한 그는 이 책에서 다음과 같은 문제를 제시하였다.
l 1월 1일에 태어난 암수 한 쌍의 토끼가 있다.
l 모든 달의 길이는 동일하다고 가정한다.
l 한 쌍의 토끼는 태어난지 두 달이 지나면 매달 두 마리의 새끼(암수)를 낳는다. 즉 첫번째 쌍은 3월 1일에 처음으로 두 마리의 새끼를 낳는다.
l 그들에게서 태어난 새끼들도 두 달이 지나면 짝을 이루어 매달 두 마리의 새끼를 낳는다.
l 어떠한 토끼도 중간에 죽지 않는다.
l 일 년 후에 전체 토끼는 모두 몇 쌍일까?
피보나치는 근친교배, 환경, 먹이, 다산, 불임 등 일어날 수 있는 여러 상황은 모두 제거하고 문제를 단순화 시킴으로써 상황 속에 숨은 원리를 파악하고자 하였다.
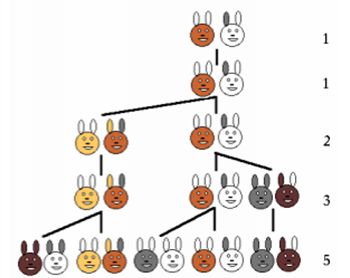
그 결과 피보나치는 매달 관찰되는 토끼의 쌍이 특정한 규칙을 따르고 있음을 발견하고 12월 말에 144쌍의 토끼를 예상하였다.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144
3. 자연계에서 발견되는 피보나치 수열
자연계에서 이러한 수열이 제법 흔하게 발견된다는 사실은 잘 알려져 있다. 여러 꽃잎의 갯수를 조사해보면 피보나치 수열이 자주 나타난다.

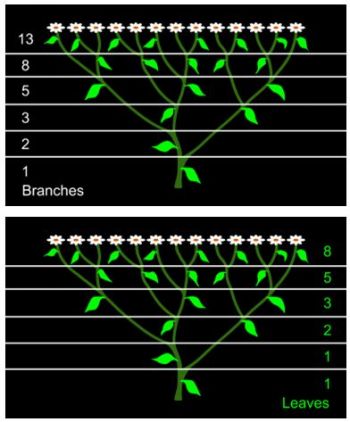
가상적으로 표현된 아래의 그림을 보면 식물 줄기의 가지와 잎의 갯수에서도 피보나치 수열이 나타난다.
아래 그림의 솔방울은 한쪽 방향으로 8개의 나선이 나타나고 다른 방향으로는 13개의 나선이 나타난다. 모두 피보나치 수열에서 나타나는 숫자들이다.

아래 그림의 파인애플은 한쪽 방향으로 13개의 나선이 나타나고 다른 방향으로는 21개의 나선이 나타난다.

아래 그림에서 해바라기 씨앗들이 이루는 나선 무늬는 양쪽 방향으로 몇 줄씩인지 세어보자.

그 외에도 과일 씨앗의 갯수도 피보나치 수열을 따르는 경우가 많다.

4. 식물계에 피보나치 수열이 흔한 이유
학자들에 따라 진화적인 측면에서 피보나치 수열의 효율성을 말하는 분들도 있지만, 식물성장의 역학적 측면에서 고찰한 의견도 있다.
우리는 이 이야기를 토끼의 번식에 관한 이야기로 시작했다. 토끼의 번식을 다시 생각해 본다면 수열의 출현은 자연스럽다. 즉 한쌍의 토끼만을 고려해보자. 그들은 평생을 살면서 매달 두 마리씩의 새끼를 낳지만 생후 2달이 되어서야 성장을 완료하기 때문에 둘째 달부터 출산이 가능하다는 것이다. 생물학적 진위를 논의함이 아니다. 수학적인 원리를 논의하는 것이다.
그렇다면 동일한 원리를 식물의 성장에 적용시키지 못할 이유가 없다. 식물의 줄기를 생각해보자. 이들이 두 갈래로 갈라지기 위해서는 (아니 좀더 정확하게 표현한다면 본 줄기에서 새끼 가지를 치는 것이 옳다고 생각하자.) 줄기의 굵기가 어느 정도 이상이어야 된다. 그리고 필요한 굵기 이상이 된 이후에는 정기적으로 가지치기를 할 수 있다. 따라서 새로 돋아난 새끼 가지도 어느 정도의 시간이 지난 후에는 정기적으로 가지를 칠 수 있다는 얘기이다. 그 원리가 토끼의 번식과 완전히 동일하다.
꽃잎의 모태가 되는 입자 (이런 표현을 써도 된다면)도 어느 정도 성장하고 나서 작은 새끼 입자 하나를 낳고(?) 그것이 다시 새로운 입자를 낳기 위해서는 특정한 시간이 필요하다고 가정한다면 꽃잎이나 씨앗의 갯수에서도 피보나치 수열이 나타나는 것에 대한 궁금증에 대한 어느 정도의 설명이 될 수 있을 것 같다.
5. 마치며
우리가 자연계에 대해서 아는 것이 너무 보잘것 없다는 사실에 전적으로 동의한다. 위에 열거한 많은 사례가 모두 동일한 원리로 확실하게 설명된다고 말하기는 어려울지도 모른다. 특히 솔방울이나 파인애플, 그리고 해바라기 씨앗에서 관찰되는 나선의 갯수에 대해서는 이들 씨앗들의 초기 분열과정에서 일어나는 (위와 비슷한) 밀고 당기는 동적 역학과정이 관여하지 않을까 정도의 추측 정도 만이 내게는 있을 뿐이다. 그러나 그러한 수열이 관찰되는 이상 그것을 무조건 우연의 일치로 생각할 수는 없다. 이러한 것들과 여기에 미처 언급하지도 못한 많은 사실에 대한 엄청난 비밀과 원리가 이 글을 읽으시는 여러분에 의해 밝혀지기를 바라는 마음 간절하다. 혹시 이 모든 것이 누군가에 의해 이미 명백하게 밝혀져 거의 모든 사람들이 아는 상식이 되어버린지 오래인데 나만 모르고 있었다면 나의 무지에 대한 용서를 구하며…
피아노 건반의 한 옥타브 사이에는 5개의 까만 건반, 8개의 하얀 건반, 모두 13개의 건반이 있다. 우연인가? 어린 시절 아카시아 같은 나뭇잎을 하나씩 떼어내며 여러 가지 운을 물었던 기억이 있다. 서양에도 비슷하게 꽃잎을 떼어내며 운을 묻는 경우가 있나보다. 피보나치 수열을 알고 있다면 사랑을 얻을 수도 있지 않을까?

He loves me. He loves me not. He loves me.…
(위 사진들과 그림들은 인터넷의 여러 곳에서 찾아 편집한 것입니다)
2010년 8월 1일 (큰 아들의 스물 세번째 생일을 축하하며…)
빗줄기././
[출처] 자연계의 피보나치 수열|작성자 빗줄기
'알고리즘 & 자료구조 > 알고리즘&자료구조' 카테고리의 다른 글
| 양의 정수 정렬 알고리즘(with 이진수 정렬) (0) | 2012.10.31 |
|---|---|
| 이진검색트리,이진삽입트리, 이진트리 정렬 (0) | 2012.10.31 |
| 재귀호출의 요건 (0) | 2012.10.31 |
| 수식트리(Parse Tree) (0) | 2012.10.31 |
| 스택을 이용한 전위 순회 (트리) (0) | 2012.10.31 |

