참고)
http://en.wikipedia.org/wiki/Convex_hull
요렇게 stage에 무작위로 찍은 점들이 있다치자.
원기둥 쯤으로 생각하고 원기둥들을 실로 감싸면 아래 그림처럼 될 것이다. 가운데쯤 있는 원기둥은 강력접착제로 붙이지 않고는 차례가 돌아가지 않을 것이다.
위 원기둥이 그저 눈에 보이라고 그려 놓은 것이고 크기가 없는 점이라고 하면 다음과 같이 될 것이다.
오목한 부분이 없는 폴리곤 형태다. 그래서convex hull이라 부르는게 아닐까 싶다.
기하알고리즘들이 그렇듯 눈으로 보면 대충 알겠는데 이걸 코드로 바꾸려면… 어렵다.
Convex hull관련 알고리즘도 굉장히 여러가지가 있고 그럭저럭 쉽게 이해한 Graham Scan 방식을 설명해보려한다.
- 첫 시작점을 어떤걸로 정할지
- 둘러칠 점의 순서는 또 어떻게 정할지
- 요 점이 내부에 포함될 점인지 아니면 외곽에 해당하는 점이지는 어떻게 알아낼지
3가지가 핵심이다.
GrahamScan은 시작점과 다른 모든 점이 이루는 각도를 가지고 가장 작은 각에서 가장 큰 각을 순서로 선을 잇는다.
시작점은 가장 상하좌우 가장 끝에 있는 걸 고른다.
이렇게 얻은 각도를 로 양의 정수로 고쳐서 소팅하거나 (Math.atan2의 경우 마이너스 값이 나올 수도 있다.)
양의 각도, 음의각도 두개를 따로 소팅한 뒤 합치는 것도 방법일 수 있겠다.
플래시에서는 맨 좌측에 있으면서 가장 위에 있는 녀석을 고르는 것이 각도 구할 때 유리할 것이다. 음의 각도가 나오지 않는다.
선을 이어나가는 방향은 ccw나 cw 한방향을 만족시켜야 되는데... 무슨 말인가 하면:
1번그림처럼 시계방향으로 회전한 다음 시계반대방향으로 회전하게 되면 오목한 부분이 생긴다는 말이다.
2번에서 시계반대방향이 생긴경우 해당 점을 제외시킨다.
3번 그림처럼 다음 점과 방향검사를 한다. 처음 시도한 방향과 같으면 선을 연결한다.
이러한 방향은 두 벡터의 외적으로 쉽게 알 수 있다. 외적의 값이 0이면 collinear(공선벡터: 스칼라 값은 다르더라도 방향이 같다)이고 음수이면 왼쪽(cw:시계방향)으로 돌고 양수이면 오른쪽(ccw:반시계방향)으로 돈다.
그럼 시작점을 찾아보자.
시작점과의 각도를 구한다. (시작점이 원점이 되도록 한다.)
http://blog.naver.com/helloktk/80050600334
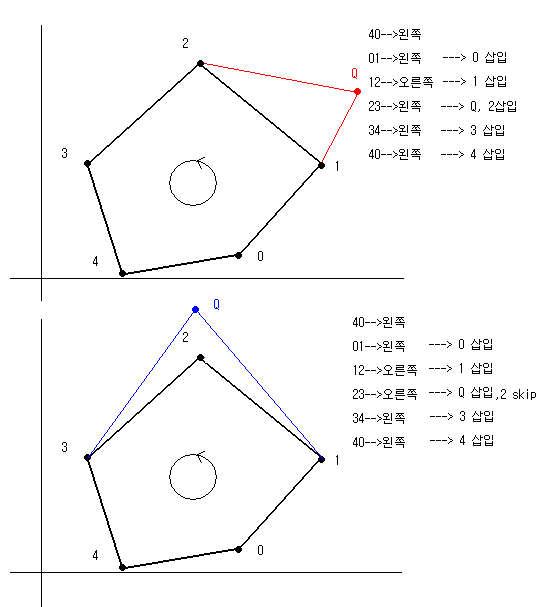
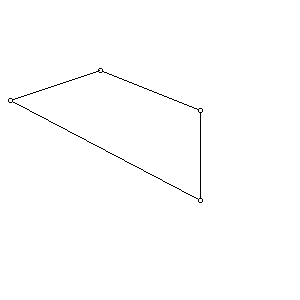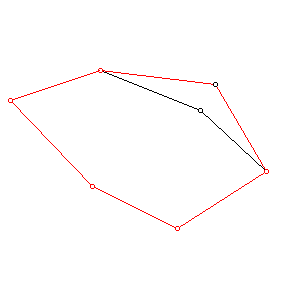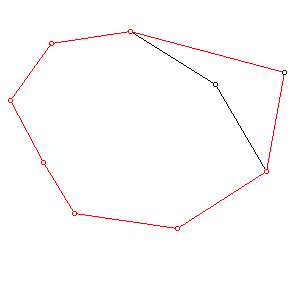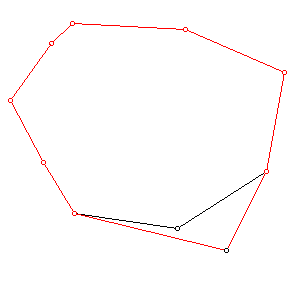
주어진 convexhull (counterclockwise)에 임의로 한 점을 추가하여 새로운 convexhull 를 구성하는 procedure 다. 작동의 원리는 아래의 그림과 같다. 만약에 주어진 점이 convexhull 의 내부점이면 원래의 convexhull이 반환된다.
std::vector<CPoint>
chull_point_merge(CPoint Q, std::vector<CPoint>& chull) {
std::vector<CPoint> out;
int n = chull.size();
if(n < 2) {
out = chull; out.push_back(Q);
return out;
}
bool pushed = false;
bool prev = isright(chull[n-1], chull[0], Q) ;
for(int i = 0; i < n; i++) {
bool curr = isright(chull[i], chull[(i+1)%n], Q) ;
if(prev) {
if(curr) {
if(!pushed) {
out.push_back(Q);
pushed = true;
}
continue;
}
else if(!pushed) {
out.push_back(Q);
pushed = true;
}
}
out.push_back(chull[i]);
prev = curr;
}
return out;
}
//C is on the right side of segment AB ;
bool isright(CPoint A, CPoint B, CPoint C) {
B -= A;
C -= A;
return (B.x * C.y - B.y * C.x) < 0 ;
}
[출처] convexhull에 점 추가.|작성자 드라곤
'알고리즘 & 자료구조 > 3D알고리즘&자료구조' 카테고리의 다른 글
| '마인 크래프트' (영상) (0) | 2013.01.26 |
|---|---|
| 심플 다각형, 컨빅스홀 결과화면들.. (0) | 2012.10.31 |
| simple polygon (0) | 2012.10.31 |
| 불꽃, 유체 시뮬레이션 링크들 (0) | 2012.10.27 |
| 파티클 시스템 링크들 (0) | 2012.10.27 |






