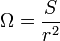1. 호도법, 평면각(라디안,rd), 입체각(스테라디안,sr) 이란?
※ 호도법 (Circular Measure)
- 일반 각도법으로는, 무리수 표현이 어려워지는 등, 여러가지로 불편하여,
- 길이 비율에 따라 각도를 표현하는 방법
ㅇ 평면각 (Plane Angle) (라디안)
- 두 `길이`의 비율로 표현되는 각도
ㅇ 입체각 (Solid Angle) (스테라디안)
- `넓이`와 `길이의 제곱`과의 비율로 표현되는 각도
2. 평면각(라디안) 및 입체각(스테라디안)의 단위 [ SI 단위계의 보조단위 ]
※ 평면각,입체각은 순수한 수(數)로 된 단위로써 사실상 무 차원의 물리량이나,
- 호도법 표기를 강조하기 위해 단위를 각각 radian, steradian 으로 씀
ㅇ radian : 평면각의 단위 [rad]
- 1 radian 은,
. 반지름과 동일한 호의 길이가 품는 각도
.. 즉, 원주 상에서 그 반경과 같은 길이의 호를 끊어서 얻어진,
.. 2개의 반경 선 사이에 낀 (평면의) 각을 말함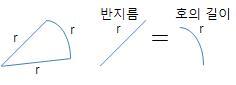
- 반지름 r인 원에서, 호의 길이 s인 평면각은, α = s / r = 원주 길이 / 반지름 길이
- 일반 각도 및 라디안의 관계는,
. 완전한 원은 원주 길이가 2πr 이므로, 2πr/r [rad]= 2 π [rad] = 360 [˚]
- 例) 원 전체 원주(1원주) => 2π[rad] = 360[˚] => 1 [rad] = 180/π[˚] ≒ 57.2958[˚]
ㅇ steradian : 입체각의 단위 [sr]
- 1 steradian 은,
. 단위 구에서, 구면 상의 단위 면적을 품는 입체 각도
. 또는, 구의 반경의 제곱과 같은 표면적에 해당하는 공간 입체 각도
.. 구의 중심을 정점으로한 구표면에서 그 구의 반경을 한 변으로 하는,
.. 정사각형 면적(r²)과 같은 곡면 표면적(r²)을 갖는 공간적인 각을 말함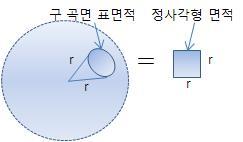
- 반지름 r인 구에서, 표면적 A에 해당하는 입체각은, ω = A / r2
- 例) 전 구의 입체각은,
. 구의 전 표면적이 4πr²이므로, 4π [sr]
3. 구의 미소 면적 및 미소 입체각(differential solid angle) (구좌표계에서)
ㅇ 구 전체 표면적 A = 4πr2 [㎡]
ㅇ 미소 면적소 dA = r2 sinθdθdΦ [㎡]
ㅇ 미소 입체각 dΩ = sinθdθdΦ [sr]
입체각
공간에서 O를 한 끝점으로 하는 사선(射線:ray) OA가 O의 둘레를 회전하여 처음의 위치로 되돌아올 때, 그려진 도형을 입체각이라 하며 O를 꼭짓점이라 한다. 이 경우 입체각의 크기는 O를 중심으로 하여 반지름 1인 구(球)가 이 입체각의 변과 만나서 이루어지며, 구면 위의 도형 S의 넓이로 측정된다.
S의 넓이가 1일 때, 이 입체각을 1sr(스테라디안:steradian)이라고 한다. 이것이 입체각의 단위이며, 평면의 경우의rad(라디안:radian)의 정의를 구면 위로 확장한 것이라고 할 수 있다. 또 전 구면의 중심점에 대한 입체각의 1/(4π)이 1sr이 된다.
[네이버 지식백과] 입체각 [solid angle, 立體角] (두산백과)
출처 : 위키
스테라디안
스테라디안(steradian, 기호 sr)은 입체각의 국제 단위이다. 평면에서 각도를 나타내는 라디안처럼, 3차원 공간에서 각도로 나타나는 2차원의 영역을 나타낼때 사용된다. 용어는 견고함을 의미하는 그리스어: στερεός
스테레오스[*]와 광선을 의미하는 라틴어: radius
라디우스에서 유래한다.
스테라디안은 라디안 처럼 무차원상수이다. 즉, 1 sr = m2·m-2 = 1. 구 전체의 입체각은 4 sr이 된다.
sr이 된다.
정의[편집]
1 스테라디안은 반지름이 r인 구의 표면에서 r2인 면적에 해당하는 입체각이다.
면적 A가 r2 와 같고, 반구의 표면적 (

)과도 같다면,
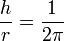
이 관계를 따르게 된다. 그러므로, 각

를 갖는 콘의 입체각은 다음과 같아진다.
이것은 축으로부터의 각(apex angle)의 2

≈ 1.144 rad or 65.54°에 대응된다.
구의 면적이
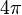
r2이므로, 정의에 의해 구는 4

=12.56637 스테라디안이다. 같는 논리로, 최대 입체각은 4

sr 이다. 스테라디안은 squared radian으로 불리기도한다.
스테라디안은 1 라디안의 angle excess(angle excess)를 갖는 다각형의 구면, 또는 완전한 구의 1/(4

), 또는 (180/

)2 제곱 각(square degree), 또는 3282.80635 제곱 각과 같다.
스테라디안은 SI 보조 단위였으나, 1995년 SI 보조 단위가 폐지 되면서, SI 유도 단위가 되었다.
라디안과 유사성[편집]
2차원 평면에서, 라디안으로 표현되는 각은 잘려지는 호의 길이와 관련이 있다.
-
- l 은 호의 길이
- r 은 원의 반지름.
3차원에서, 스테라디안으로 표현되는 입체각은 잘려지는 면적과 관련이 있다.
-
- S 은 표면적
- r 은 구의 반지름.
http://goo.gl/QgJXjg
1스테라디안(1sr)은 몇도인가요??
호도법의 360도는 라디안으로 고치면 2∏ 라디안이 됩니다.
따라서 1라디안 = 360/2∏ 이고 ∏는 3.14정도되므로 1라디안 = 57.32도 정도가 됩니다.
스테라디안은 원의 각도를 나타내는 단위가 아니고 구(공)의 각도를 나타내는 단위입니다.
즉, 구 반지름의 제곱과 같은 구 표면적에 대응하는 구의 입체각으로 정의됩니다.
예를들어 공의 반지름이 1m 라고 하면 반지름의 제곱은 1m^2 가 됩니다.
공의 표면상에 한면이 1m인 정사각형을 그리고 이 정사각형의 각 꼭지점에서 공의 중심까지
선을 그린다고 하면 4개의 선이 공의 중심에서 만나게 됩니다. 이때 이 4개의 선이 만든
입체각을 나타내는 단위가 스테라디안입니다.
구의 표면적은 잘 알려져있다시피 4∏r^2 입니다. 여기서 r은 구의 반지름이지요.
따라서 구의 중심각은 4∏가 됩니다. (원의 중심각은 360도 인것처럼)
|
Solid Angle (입체각)
|
기본 개념
평면각이 평면에서의 퍼짐 정도를 나타내는 척도의 개념이라면 입체각은 말 그대로 공간에서의 퍼짐 정도를 나타내는 척도로서의 각도이다. 이러한 공간에서의 퍼짐을 표시하는 각도의 개념은 등방위성으로 퍼지는 현상, 예를 들어 점원(point source)으로부터의 빛, 전파, 방사선이 발산될때의 세기를 기술하는 데 아주 유용한 도구가 된다.
아래 그림에서 점0에 점광원이 놓여져 있을 때, 비록 면‘가’와‘가`’는 서로 면적의 형상 및 크기가 다르지만 두 면 다 빛의 동일한 퍼짐 각도 이내에 있기에 이 두 면에 도달하는 빛 에너지의 합은 같게 된다. 이와같이 이러한 의미로 정의되는 각도를 공간에서 정의하면 공간에서의 세기와 같은 문제를 쉽게 다룰수 있는 도구가 된다.

(그림1 입체각의 개념 및 투영)
입체각의 정성적 및 정량적 정의
이러한 기능의 개념인 입체각의 정의는?
이의 정성적 정의는 위에서 설명한 그대로 공간에서의 퍼짐을 표시하는 척도.
실제사용을위해서는?
정량적 정의가 필요
정량적 정의의 이해를 위해서 먼저 위의 정성적 정의의 입체각 성격을 보면,
이 각도는 점원으로부터 공간의 어느 지점까지의 거리에 반비례하고,
좀더 정확히 이야기하면 거리의 제곱에 반비례하고, 또 그 지점에서 얼마나 펼쳐지는 가에 비례함을 알 수 있다.
즉 이러한 특성에 따라 입체각의 크기를 다음 식과 같이 정량적으로 정의하면 필요한 특성을 지니게 된다.

...... 1)
그런데 이 식에서 면적은 점원에 기울어진 면적이 아니라 점원으로부터 그 면까지 그려지는 선분에 수직한 면적이어야만 위에서 이야기된 입체각에 요구된 특성이 만족될 수 있다. 즉,

........ 2)
이를 vector 연산식으로 표시하면 표현은 매우 간단해지는 데, 미소면적 dA에 대한 입체각 dΩ는,

........ 3)
n 은 해당 면의 단위 표면 vector, dA는 수직성분 여부와 관련없이 그 면의 실제크기, r은 점원에서 해당 면까지의 거리 vector
식2) 또는 대등하게 식3)이 고체각에 대한 정량적 정의다. 참고로, 3)에서 분모의 r의 지수가 2가 아닌 3이지만 분자에 r이 있기에 결국은 앞에서 식2) 와 같이 r의 지수는 2가 된다.
정의식 식3) 을 이용하여 미소면적이 아닌 유한 면적에 대해 적용하고 , 식3) 의 vector연산을 간략히 하기 위하여 적용면적에 투영 면적의 개념을 적용한다. 달리 표현하면 그 면의 거리 vector r 에 대해 수직하면서 동일한 고체각도인 면에 대해 적용한다.
즉 그림 1)의 면 '나'는, 면 '가'를 동일 원점을 중심으로 하는 구에 투영시킨 면이고 이 두 면은 공간에서 퍼짐의 정도가 서로 같기에 고체각 역시 서로 같다. 따라서 면 '나'에 대한 고체각 작업 결과는 '가'에 대한 결과와 동일. (단, 그림에서는 두 면의 개념상의 차이를 나타내기 위해 면 '가'와 '나'의 r 이 서로 다르게 그려져있는 데, 이해를 쉽게 하기 위해 면 '나'를 당겨와 r 이 면 '가'의 r 이 되는 지점에 면 '나'가 위치한 것으로 상정한다.)
면 '나'에서

....... 4)
식 4) 를 식 2) 또는 식 3)에 대입하면,

.......... 5)
식 5) 로부터 알 수 있듯이 입체각은 무차원인데 편의상 steradian 단위 또는 sr이란 약자를 붙여서 표시하기도 한다.
또한 고체각이라는 용어가 사용되기도 한데 이는 입체각에 해당되는 영어표현 solid angle을 그대로 옮긴 것으로 바람직스럽지 못한 용어다.
반구에 대한 고체각은 식 5) 로 부터

....... 6)
또는 식 2)로부터도 역시 같은 결과를 얻을 수 있다.
즉, 구의 표면적 =
이기에

............................. 7)
유사하게,

입체각의 적용
고체각의 개념은 이러하고, 좀 현실적인 감을 익히기 위해 다음 그림과 같이

(그림 2. 원추의 입체각)
사이각이 θ 인 직삼각형 1-2-3을 한바퀴 회전시켰을 때 만들어지는 원추의 입체각은

........... 8)
식 8) 에 의해 몇가지 사이각θ에 대한 입체각은 다음과 같다
| 평면각 θ(도) | 입체각sr |
| 0 | 0 |
| 10 | 0.0954 |
| 20 | 0.379 |
| 30 | 0.842 |
| 40 | 1.470 |
| 45 | 1.840 |
| 60 | 3.142 |
| 90 | 6.283 (= |
| 180 | 12.6 (= |
===========================================================================================================================
[출처] : 네이버 오픈사전
네이버 스마트 에디터 수식입력기로 수식 입력... 좋은데?
띄어쓰기 및 줄 맞춤, 단어 맞춤 추가
[출처] Solid Angle (입체각)|작성자 GUNN
ref : http://www.ktword.co.kr/test/view/view.php?id=545&m_temp1=975&nav=1
'수학 (Mathematics) > 3D수학' 카테고리의 다른 글
| 파이프라인 연산 (0) | 2023.03.11 |
|---|---|
| 구현한 범프 매핑 설명(탄젠트 공간) (0) | 2014.12.09 |
| 투영행렬로 변환 한 후 다시 카메라 공간의 위치,벡터(norm) 을 구하는 방법과 d3dx9math.h (0) | 2013.07.09 |
| 점,벡터 구분의 미묘함 (0) | 2013.05.08 |
| 쿼터니온을 사용해 오브젝트 회전시키기 (0) | 2013.04.24 |