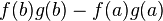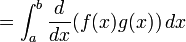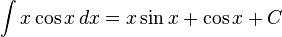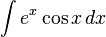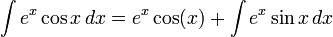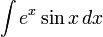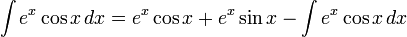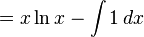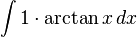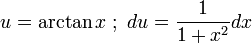3DMP engines

3D그래픽스 물리 수학, 프로그래밍 GPU Shader 게임엔진 알고리즘 디자인패턴 matlab etc..

연속 부분적분 = 이해를 돕기위해 그냥 이름 붙인것..

미분은 첫번째 pass 두번째 부터

적분은 첫번째 부터 하고 마지막 ∫ dx 안에 넣을때 미분한것은 처음에 않했음으로 미분해서 들어가지만 적분한

것은 처음부터 적분했음으로 마지막 ∫ dx 안에는 적분하지 않은 상태로 들어간다

부분적분법에서

u' 을 d에 넣어 du

v' 을 d에 넣어 dv

의 형태로 바꿔놓고 풀면 더욱 간단하다

이하 첨부파일과 자세한 내용이다

부분적분공식정리.pdf

부분적분
위키백과, 우리 모두의 백과사전.
미적분학
함수의 극한
연속함수
다항식의 미적분
기본 정리
텐서 미적분학
[보이기]미분
[보이기]적분
[보이기]벡터 미적분학
v • d • e • h
미적분학에서 부분 적분은 어떤 함수들의 곱에 대한 적분을 간단한 적분으로 변환하는 방법이다. 직접 적분하기 어려운 함수를 적분하기 쉬운 함수로 변환하는데 그 목적이 있다. 이 방법은 미분의 곱셈 법칙에서 유도할 수 있다.
목차
[숨기기]
1 법칙
2 예제
2.1 x cos x의 적분
2.2 e^x cos x 의 적분
2.3 ln x 의 적분
2.4 arctan x의 적분
3 문제 해결의 전략
4 주석
[편집]법칙
두 미분가능한 연속 함수 $f (x)$ 와 $g (x)$ 에 대해서, 적분 구간이 $[a, b]$ 일 때, 부분적분법은 다음과 같이 표현할 수 있다.
$\int_a^b f(x) g'(x)\,dx = \left[ f(x) g(x) \right]_{a}^{b} - \int_a^b f'(x) g(x)\,dx$
이때 우변의 첫째 항은 다음을 나타낸다.
$\left[f(x) g(x) \right]_{a}^{b} = f(b) g(b) - f(a) g(a).$
이 법칙은 다음과 같이 미분의 곱셈 법칙과 미적분학의 기본정리로 증명할 수 있다.
$f(b)g(b) - f(a)g(a)\,$ $= \int_a^b \frac{d}{dx} ( f(x) g(x) ) \, dx$
$=\int_a^b f'(x) g(x) \, dx + \int_a^b f(x) g'(x) \, dx$
부정적분의 경우에는 다음과 같다.
$\int f(x) g'(x)\,dx = f(x) g(x) - \int g(x) f'(x)\,dx$
또는, 짧게 줄여서 다음과 같이 표현하기도 한다.
$\int u\,dv = u v - \int v\,du$
여기서, $u = f(x),\ v = g(x)$ 이고, $du = f'(x) dx,\ dv = g'(x) dx$ 이다.
[편집]예제
[편집]x cos x의 적분
다음 식을 적분한다.
$\int x\cos x \,dx$
이때, $u = x,\ du = dx,\ dv = \cos x \, dx,\ v = \sin x$ 와 같이 가정하면
$\int x\cos x \,dx$ $= \int u \,dv$
$= uv - \int v \,du$
가 되어,
$\int x\cos x \,dx = x\sin x - \int \sin x \,dx$
$\int x\cos x \,dx = x\sin x + \cos x + C$
와 같이 적분을 풀 수 있다. 이때, $C$ 는 적분 상수이다.
[편집]e^x cos x 의 적분
$\int e^{x} \cos x \,dx$
이 경우는 부분 적분법을 두 번 사용한다. 먼저 다음과 같이 가정한다.
$u = \cos x, du = -\sin x \, dx$
$dv = e^x dx,\ v = e^x$
이때,
$\int e^{x} \cos x \,dx = e^{x} \cos (x) + \int e^{x} \sin x \,dx$
이고, 우변의 항에 대해서 다시 한 번 적분한다. 다음과 같이 가정한다.
$u = \sin x\;;\ du = \cos x \, dx$
$v = e^x\;;\ dv = e^x dx$
그러면,
$\int e^{x} \sin x \,dx$ $= e^{x} \sin x - \int e^{x} \cos x \,dx$
이므로, 함께 적으면,
$\int e^{x} \cos x \,dx = e^{x} \cos x + e^x \sin x - \int e^{x} \cos x \,dx$
임을 알 수 있다.
자세히 살펴 보면, 좌변의 적분항이 오른쪽에도 동일하게 나타나는 것을 확인 할 수 있다. 따라서 우변의 적분 항을 좌변으로 다음과 같이 보내면,
$2 \int e^{x} \cos x \,dx = e^{x} ( \sin x + \cos x )$
이고, 2로 나눠
$\int e^{x} \cos x \,dx = {e^{x} ( \sin x + \cos x ) \over 2}$
와 같은 결과를 얻을 수 있다.
[편집]ln x 의 적분
또 다른 예제로, 어떤 함수를 1과 그 자신의 곱으로 생각해 부분 적분을 적용하는 경우가 있다. 이 방법은 적분을 구하고자 하는 함수의 미분값과 이 미분값에 $x$ 를 곱한 함수의 적분값을 알고 있는 경우에 유용하다.
첫 번째 예는, $\int \ln x \,dx$ 이다.
위 식은 다음과 같이 나타낼 수 있다.
$\int (\ln x) \cdot 1 \,dx$
다음과 같이 가정하면,
$u = \ln x\;;\ du = \frac 1 x dx$
$v = x\;;\ dv = 1 \cdot dx$
$\int \ln x \,dx$ $= x \ln x - \int \frac{x}{x} \,dx$
$= x \ln x - \int 1 \,dx$
$\int \ln x \,dx = x \ln x - {x} + {C}$
$\int \ln x \,dx = x ( \ln x - 1 ) + C$
이고, 이 식에서 C는 적분 상수이다.
[편집]arctan x의 적분
두 번째 예는 $\int \arctan x \,dx$ 이다. 여기서 $arctan$ 함수는 역 탄젠트 함수를 의미한다. 이 식 역시 다음과 같이 나타낼 수 있다.
$\int 1 \cdot \arctan x \,dx$
다음과 같이 가정하면,
$u = \arctan x\;;\ du = \frac 1 {1+x^2} dx$
$v = x\;;\ dv = 1 \cdot dx$
$\int \arctan x \,dx$ $= x \arctan x - \int \frac{x}{1 + x^2} \,dx$
$= x \arctan x - {1 \over 2} \ln \left( 1 + x^2 \right) + C$
임을 확인 할 수 있다.