라플라스 변환, 도함수의 라플라스변환, 변환의 미분, 합성곱, 주기함수의 변환, 역변환

2012. 11. 3. 12:26

첨부파일 :

라플라스.alz

이하 퍼온글

라플라스 변환(Laplace transform)은 어떠한 함수 $f (t)$ 에서 다른 함수로의 변환으로, 선형 동역학계와 같은 미분 방정식을 풀 때 유용하게 사용된다. 피에르시몽 라플라스의 이름을 따 붙여졌다.

라플라스 변환을 이용하면, 어려운 식들을 쉽게 변환하여 풀 수 있으며, 문제들을 직접적으로 해결 할 수 있는 장점이 있다. 초기값 문제의 경우 일차적으로 일반해를 구하는 단계가 필요없게 되고, 비제차 미분방정식의 경우에는 대응하는 제차미분방정식을 먼저 풀 필요가 없다. 라플라스 변환은 주어진 식은 간단한 식으로 변환한 뒤, 변형된 식을 푼다. 그리고 그렇게 풀어진 해를 다시 원식으로 변환한다.

라플라스 변환 : t 관련 값이 들어가 s 관련 값이 나온다

정의

함수 $f (t)$ 의 라플라스 변환은 모든 실수 t ≥ 0 에 대해, 다음과 같은 함수 $F (s)$ 로 정의된다.

$F(s)&#-3;&#-0; = \mathcal{L}\left\{ f\right\}(s)&#-3;&#-0; =\int_{0^-}^\infty e^{-st} f(t)\,dt.$

여기서 $0 -$ 는 $\lim_{\epsilon \rightarrow +0} -\epsilon$ 를 간단히 나타낸 것이고 복소수 $s = \sigma + i \omega \,$ , σ와 ω는 실수이다.

실제 사용시에는 엄밀히 정확하지는 않지만 $F(s) = \mathcal{L} \left\{f(t)\right\}$ 로 표기하기도 한다.

위 정의대로 풀때 무한대 기호가 있기 때문에 이상적분으로 풀이를 하지만 간편하게 그렇다고 인지하고 있고 그냥

풀어 나간다, 너무 자세한건 오히려 보기 지저분할 수 있다

성질

선형성

$\mathcal{L}\left\{a f(t) + b g(t) \right\}&#-3;&#-0; = a \mathcal{L}\left\{ f(t) \right\} +&#-3;&#-0; b \mathcal{L}\left\{ g(t) \right\}$

상수는 Laplace 밖으로 빠질 수 있다

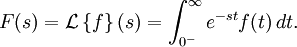
$F(s)&#-3;&#-0; = \mathcal{L}\left\{ f\right\}(s)&#-3;&#-0; =\int_{0^-}^\infty e^{-st} f(t)\,dt.$

미분

$\mathcal{L}\{f'\}&#-3;&#-0; = s \mathcal{L}(f) - f(0)$ = sF(s) - f(0)

$\mathcal{L}\{f''\}&#-3;&#-0; = s^2 \mathcal{L}(f) - s f(0) - f'(0)$ = s^2F(s) - sf(0) - f'(0)

$\mathcal{L}\left\{ f^{(n)} \right\}&#-3;&#-0; = s^n \mathcal{L}\{f\} - s^{n - 1} f(0) - \cdots - f^{(n - 1)}(0)$

$\mathcal{L}\{ t f(t)\}&#-3;&#-0; = -F'(s)$ = - d/ds F(s)

t^2 라면

- ( - ) d/ds d/ds F(s) = + d^2/ds^2 F(s)

$\mathcal{L}\{ t^{n} f(t) \}&#-3;&#-0; =(-1)^{n} F^{(n)} (s)$ = (-1)^n d^n/ds^n F(s)

'L{ } ' is laplace

$\mathcal{L}\left\{ \frac{f(t)}{t} \right\} = \int_s^\infty F(\sigma)\, d\sigma$ , L{ f(t) } = F(σ)

적분

'*' is convolution , "합성곱"

tip : T is not t

L { 1 * f(t) } = $\mathcal{L}\left\{ \int_0^t f(\tau)\, d\tau \right\} = \mathcal{L}\left\{ u(t) * f(t)\right\} = {1 \over s} F(s)$

합성곱 ( '*' is convolution , "합성곱" )

(f * g)(t) = ∫ f(u)g(t-u) du , 적분범위는 0(아래 끝) ~ t(위 끝) 까지

$\mathcal{L}\{f * g\}&#-3;&#-0; = \mathcal{L}\{ f \} \mathcal{L}\{ g \}$

t shifting

u( t - a) = 단위계단 함수(= 층계 함수)

t <= a 라면 u(t-a) = 0

t > a 이면 u(t-a) = 1

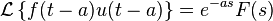
$\mathcal{L}\left\{ f(t - a) u(t - a) \right\}&#-3;&#-0; = e^{-as} F(s)$

$\mathcal{L}^{-1} \left\{ e^{-as} F(s) \right\}&#-3;&#-0; = f(t - a) u(t - a)$

참고: $u (t)$ 는 층계 함수이다.

합성곱

$\mathcal{L}\{f * g\}&#-3;&#-0; = \mathcal{L}\{ f \} \mathcal{L}\{ g \}$

주기가 p인 주기함수의 라플라스 변환

$\mathcal{L}\{ f \}&#-3;&#-0; = {1 \over 1 - e^{-ps}} \int_0^p e^{-st} f(t)\,dt$

라플라스 역변환( s 관련 값이 들어가 t 관련 값이 나온다 )

An integral formula for the inverse Laplace transform, called the Bromwich integral, the Fourier–Mellin integral, and Mellin's inverse formula, is given by the line integral:

$\mathcal{L}^{-1} \{F(s)\} = f(t) = \frac{1}{2\pi i}\lim_{T\to\infty}\int_{\gamma-iT}^{\gamma+iT}e^{st}F(s)\,ds,$

http://pinkwink.kr/173

라플라스 변환

위에 라플라스변환의 정의가 나타나 있습니다.

라플라스변환의 정의를 이용해서 "1"을 라플라스변환한 결과입니다. 그러나, 위 정의식을 계속 사용한다는 것은 뭐 힘든일이겠지요^?^. 그래서

저와 같이 변환표를 이용합니다.

라플라스 역변환

위는 라플라스 역변환표입니다. 뭐 당연히 라플라스 변환표의 반대겠지요^^. 라플라스 역변환의 정의는 아주 복잡해서 손으로 푸는 것은 어렵습니다. 그래서 위 역변환표에 가장 가까운 형태로 식의 형태로 바꾸어가는 겁니다.

위의 예제를 보면 무슨 말인지 알 수 있을겁니다.

위 예제는 항별나누기를 이용해서 식을 분리하고, 라플라스 변환이 가지는 선형성을 이용해서 각각을 역변환하는 것입니다.

위 예제는 흔히 말하는 유수정리(Residue Theorem)의 부분분수 전개를 이용한 것입니다. 보통은 위 전개방식은 분모를 영으로 만드는 것을 대입한다고 외웁니다.^^.

이 라플라스 변환과 역변환은 미방의 풀이에 큰 장점을 가지게 되는데요 일단 도함수를 변환하면 위 정리와 같습니다.

미방을 라플라스 변환하고 대수방정식화된 식의 해를 찾고 다시 역변환하는 과정을 거치게 됩니다.

위 간단한 예를 보면

위와 같이 초기값을 고려하여 라플라스변환하고 라플라스변환된 식을 푼다음 다시 역변환으로 그 해를 찾는 것입니다.

Translation Theorem

시간영역에서 지수함수는 라플라스 변환을 하고 나면 단순 평행이동이 되어있습니다.

이를 이용하면 위 예제들 역시 간단히 그 해를 찾을 수 있습니다.

참고자료:
Laplace Transform -3.pdf

Derivatives of Transforms

시간영역에서 시간의 급수형태의 함수를 라플라스변환하면 라플라스 도메인 영역에 대한 미분형태로 나타나게 됩니다.

저작자표시 비영리 동일조건

'수학 (Mathematics) > 공업수학' 카테고리의 다른 글

적분 12 : 고급 정적분 테크닉 - 미분 (1) (0)	2012.11.03
단위계단함수 (0)	2012.11.03
비선형 미분방정식 [기초] (0)	2012.11.03
비감쇠 강체운동 미분방정식(상계수미방-미정개수법으로 풀이) (0)	2012.11.03
치환을 활용한 비동차(비제차) 미분방정식 ( 코시 오일러 미방, 매개변수변환법 ) (0)	2012.11.03

3DMP